Capacidades Caloríficas

Referência : Lage, E., (2019) Capacidades Caloríficas, Rev. Ciência Elem., V7(2):032
Autor: Eduardo Lage
Editor: José Ferreira Gomes
DOI: [http://doi.org/10.24927/rce2019.032]

---

A Capacidade Calorífica de um corpo é a quantidade de calor que é necessário fornecer-lhe para elevar a sua temperatura de uma unidade. Por outras palavras, é a quantidade de energia (na forma de calor) fornecida ao corpo dividida pela grandeza da variação da sua temperatura.

O conceito de capacidade calorífica é um dos mais importantes e mais antigos em Termodinâmica. A designação provém da velha teoria do calórico para a qual o calor era um fluido que passava de um corpo para outro e onde a quantidade trocada dependia das capacidades de armazenamento desse fluido que os corpos apresentariam. O calórico há muito foi abandonado, mas ficou o conceito de capacidade ($C$), a medida (unidade no S.I.: J/K) da quantidade de calor ($\delta Q$) que se tem de fornecer a um corpo para lhe originar uma elevação de temperatura $\delta T$: $C=\frac{\delta Q}{\delta T}$, i.e., quantos Joules são necessários para elevar de 1K a temperatura da substância. Alguns exemplos, referidos a 1Kg: aço (460), granito (800), vidro (40), água (4184). Quando referida a 1 Kg, a capacidade calorífica designa-se por calor específico ou capacidade calorífica mássica. Note-se que, para a água, este resultado é exato porque é a definição da Kcal (1000 calorias). Esta definição é, contudo, insuficiente por ser necessário especificar as condições a que o sistema está sujeito quando recebe calor, sendo comum ser mantido constante o volume ($V$) ou a pressão ($p$), assim se definindo a capacidade calorífica a volume constante ($C_V$) ou pressão constante ($C_p$), respetivamente. Iremos aqui considerar a relação entre estas capacidades caloríficas e expôr o método de Rüchardt que determina experimentalmente $\gamma \equiv C_p/C_V$ em gases.

Para os sistemas simples que aqui consideramos, o estado de equilíbrio termodinâmico pode ser definido pelo volume ($V$) e temperatura ($T$), deduzindo-se a pressão a que está submetido pela equação de estado que relaciona estas três variáveis. Assim, a entropia, uma função de estado, tem $V$ e $T$ como argumentos, pelo que a sua diferencial se escreve:

$dS=\left(\frac{\partial S}{\partial T}\right)_VdT + \left(\frac{\partial S}{\partial V}\right)_TdV$            (1)

Aqui, os subscritos indicam a variável que é mantida fixa na derivação.

Comecemos por analisar o caso simples de ser mantido constante o volume. Então, quando o sistema recebe, reversivelmente, a quantidade de calor $\delta Q$, a sua entropia aumenta de $\frac{\partial Q}{T}$, pelo que:

$dS=\frac{\delta Q}{T}=\left(\frac{\partial S}{\partial T}\right)_VdT \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ C_V=\frac{\delta Q}{\delta T}=T\left(\frac{\partial S}{\partial T}\right)_V$            (2)

Suponhamos, agora, que é mantida constante a pressão. Então, a quantidade de calor que o sistema necessita receber para elevar a sua temperatura de $\delta Q$ é maior que no caso anterior porque parte desse calor é transformado em trabalho pois que, necessariamente, há aumento de volume (dilatação térmica) para ser mantida a pressão. Assim, deverá ser e $C_p\geq C_V$, usando a eq. (1) podemos relacionar estas duas capacidades:

$dS=\frac{C_V}{T} dt +\left(\frac{\partial S}{\partial V}\right)_T\left(\frac{\partial V}{\partial T}\right)_p dt$

Segue-se que a quantidade de calor recebida é:

$\delta Q =TdS=\left[C_V+T\left(\frac{\partial S}{\partial V}\right)_T\left(\frac{\partial V}{\partial T}\right)_p\right]dT \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ C_p=C_V+T\left(\frac{\partial S}{\partial V}\right)_T\left(\frac{\partial V}{\partial T}\right)_p$            (3)

A equação de estado fornece $\left(\frac{\partial V}{\partial T}\right)_p$- abaixo veremos o resultado para um gás perfeito. Mas como calcular $\left(\frac{\partial S}{\partial V}\right)_T$? Entra, aqui, todo o poder analítico da Termodinâmica: devemos procurar uma função de estado cuja diferencial se escreve à custa das diferenciais do volume e da temperatura. Essa função de estado não é a energia interna ($U$) pois que os 1º e 2º Princípios da Termodinâmica nos levam a escrever:

$dU=TdS-pdV$

Mas esta expressão sugere a forma de encontrarmos o que procuramos ¹: considere-se a função $F\equiv U-TS$, conhecida por energia livre de Helmholtz. Então:

$dF=dU-TdS-SdT=-SdT-pdV$            (4)

Esta diferencial é exata porque $F$ é uma função de estado, pelo que:

$\frac{\partial }{\partial V}\left(\frac{\partial F}{\partial T}\right)_V=\frac{\partial }{\partial T}\left(\frac{\partial F}{\partial V}\right)_T$

Ora, da eq. (4), obtemos:

$\left(\frac{\partial F}{\partial T}\right)_V=-S \ \ \ \ \ \ \ \ \left(\frac{\partial F}{\partial V}\right)_T=-p$

Pelo que a relação anterior fica ²:

$\left(\frac{\partial S}{\partial V}\right)_T=\left(\frac{\partial p}{\partial T}\right)_V$

O segundo membro é conhecido pela equação de estado. Assim, regressando à eq. (3), obtemos:

$C_p=C_V+T\left(\frac{\partial p}{\partial T}\right)_V\left(\frac{\partial V}{\partial T}\right)_p$            (5)

Esta relação aplica-se a qualquer corpo. Num sólido, por exemplo, a dilatação térmica é muito pequena e pode, muitas vezes, ser ignorada, pelo que $C_p\approx C_V$. Não é assim nos gases, como veremos adiante.

Ex.: gás perfeito

A equação de estado é $p=\frac{nRT}{V}$, onde $n$ é o número de moles e $R$ a constante dos gases perfeitos. Então:

$\left(\frac{\partial p}{\partial T}\right)_V=\frac{nR}{V} \ \ \ \ \ \ \ \ \left(\frac{\partial V}{\partial T}\right)_p=\frac{nR}{p}\ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ T \left(\frac{\partial p}{\partial T}\right)_V\left(\frac{\partial V}{\partial T}\right)_p=T\frac{nR}{V}\frac{nR}{p}=nR$

Assim:

$C_p=C_V+nR$            (6)

Que podemos dizer sobre $C_V$? O teorema da equipartição da energia informa que cada termo quadrático na energia de uma molécula contribui com $\frac{1}{2}\frac{R}{N_A}T$ para a energia média da molécula (esta não tem uma energia fixa quando em contacto com a fonte de calor à temperatura $T$). Então, para as $nN_A$ moléculas, cada termo quadrático contribui com $\frac{1}{2}nRT$. Se houver $f$ termos quadráticos na energia da molécula, e admitindo que as moléculas não interagem (gás perfeito!), segue-se que $U=f\frac{1}{2}nRT$, pelo que $C_V=f\frac{1}{2}nR$. Alguns exemplos: num gás monoatómico, é $f = 3$ porque cada átomo só contribui com a energia cinética do movimento, havendo, pois, 3 termos quadráticos correspondentes às 3 componentes da velocidade. Num gás diatómico, para além da velocidade do centro de massa (contribuindo com os mesmos 3 termos para a energia cinética), existem, agora, 2 termos adicionais associados a movimentos de rotação em torno de 2 eixos perpendiculares entre si e perpendiculares à linha que une os átomos. Assim, $f = 5$ se a molécula se comportar como um haltere rígido. Mas se admitirmos que a molécula pode vibrar como um oscilador harmónico, surgem mais 2 termos quadráticos originados nas energias cinética e potencial da “mola” que une os átomos, pelo que $f = 7$. No caso geral, somos, assim, conduzidos, pela eq. (6), à expressão:

$C_p=\frac{f}{2}nR+nR=\left(\frac{f}{2}+1\right)nR \ \ \ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ \gamma\equiv\frac{C_p}{C_v}=\frac{f+2}{f}$

A tabela seguinte mostra os valores esperados para diversos modelos.

$f$	$γ$	Modelo da molécula
3	5/3	monoatómico
5	7/5	haltere
7	9/7	Diatómica c/vibração

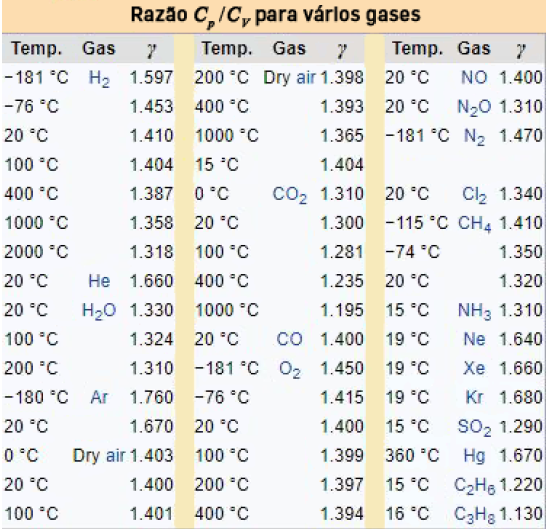
A tabela abaixo mostra valores de $γ$ obtidos experimentalmente para vários gases. Os resultados deduzidos para um gás perfeito não nos devem iludir: em geral, as capacidades caloríficas variam com a temperatura, fornecendo, desse modo, importante informação sobre o “congelamento” de graus de liberdade moleculares quando, por exemplo, a temperatura diminui. Atente-se no caso da molécula de hidrogénio: acima de 100 ºC, os valores de $γ$ sugerem um modelo haltere, mas a -181 ºC, já a molécula parece não poder rodar!

Um último exemplo considera um modelo simples de um sólido: cada átomo está ligado à sua posição de equilíbrio por uma “mola” (potencial harmónico), o que dá $f = 6$ (3 termos quadráticos na energia cinética e outros 3 termos quadráticos na energia potencial). Assim, para um mole de um sólido será de esperar $C_V ≃ 3R$, o que parece reproduzir a lei de Dulong e Petit (1819), mas apenas para temperaturas elevadas. Contudo, quando se diminui a temperatura, a capacidade calorífica molar diminui rapidamente porque é necessário considerar a quantificação destes osciladores harmónicos, como Einstein mostrou em 1907. Este é um importante tópico que aqui não será mais desenvolvido.

Voltando aos gases, admitamos que as capacidades caloríficas são constantes, independentes da temperatura. Nestas condições, podemos deduzir a equação das adiabáticas, i.e., a relação entre pressão e volume quando o sistema evolui mantendo a entropia constante. De facto, regressando à eq. (1), e com os resultados já obtidos, podemos escrever:

$dS=\frac{C_V}{T}dT+\left(\frac{\partial p}{\partial T}\right)_V dV=\frac{C_V}{T}dT+\frac{nR}{V}dV=0$

A equação integra-se facilmente, obtendo-se:

$TV^{\frac{nR}{C_v}}=const$

Ou, eliminando a temperatura pela equação de estado, tem-se a forma mais familiar:

$pV^{1+\frac{nR}{C_V}}=pV^\gamma=const$            (7)

Um método experimental para a determinação direta de $γ$ foi apresentado por Eduard Rüchardt (FIGURA 1), em 1928.

O dispositivo (FIGURA 2) consiste num grande balão onde se introduz o gás a investigar. O balão liga ao exterior através de uma longa coluna cilíndrica de vidro (diâmetro interno $2R$) colocada verticalmente. Uma esfera (ou um cilindro) maciça, de aço, de massa $m$ e com um raio muito ligeiramente inferior ao do tubo, é introduzida neste.

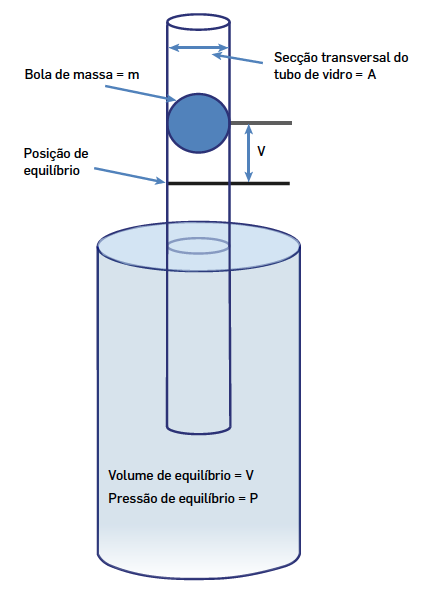
Ignorando o atrito existe uma posição de equilíbrio para a esfera quando a força devida à pressão do gás no balão igualar a soma do peso da esfera com a força devida pela pressão atmosférica. Tomando o eixo $z$ vertical e designando por $z = 0$ a cota desta posição de equilíbrio, então deve ser:

$\pi R^2p(0)=mg+\pi R^2 p_a$

Que acontece quando a esfera é afastada desta posição? Se a esfera descer, comprime o gás dentro do balão, aumentando a pressão que ele exerce e, portanto, a esfera será empurrada para $z = 0$; se a esfera subir, aumenta o volume ocupado pelo gás, o que diminui a pressão que ele exerce e, portanto, a esfera será puxada para $z = 0$. Assim, se a esfera for largada verticalmente no interior do tubo, ficará a oscilar, podendo medir-se o período da oscilação, deduzindo-se a partir daí o valor de $γ$. Com efeito, as compressões e expansões do gás são tão rápidas que o gás, praticamente, não troca calor com o exterior, i.e., evolui adiabaticamente. Assim, designando por $p(z)$ e $V(z)$, respetivamente, a pressão exercida pelo gás e o volume que ocupa quando a esfera está à cota $z$, tem-se, pela eq. (7).

$p(z)V(z)^\gamma =p(0)V(0)^\gamma \ \ \ \ \Leftrightarrow \ \ \ \ p(z)=p(0)\left[\frac{V(0)}{V(z)}\right]^\gamma$

Ora, $V(z)=V(0)+\pi R^2z$, pelo que:

$p(z)=p(0)\left[1+\frac{\pi R^2z}{V(0)}\right]^{-\gamma}\simeq p(0)\left[1-\gamma\frac{\pi R^2z}{V(0)}\right]$

onde se admitiu $V(0)>>\pi R^2z$ porque o balão é grande e as oscilações têm pequena amplitude. Assim, as forças que atuam na esfera têm resultante vertical

$\left[p(z)-p_a\right]\pi R^2-mg=\left[p(z)-p(0)\right]\pi R^2\cong-p(0)\gamma\frac{(\pi R^2)^2}{V(0)}z$

tendo, a primeira igualdade sido obtida por eliminação do peso através da condição de equilíbrio. Assim, a lei fundamental da dinâmica dá, para o movimento da esfera:

$m\frac{d^2z}{dt^2}=-p(0)\gamma\frac{(\pi R^2)^2}{V(0)}z$

É a equação de um oscilador harmónico que, portanto, apresenta a frequência (angular):

$\omega= \sqrt{p(0)\gamma \frac{(\pi R^2)^2}{mV(0)}}$

Com $p(0)$ determinado pela posição de equilíbrio, $V(0)$ praticamente igual ao volume do balão, obtemos assim $γ$ medindo o período $\frac{2\pi}{\omega}$ das oscilações da esfera.

Notas

¹ A passagem de $U$ para $F$ é uma transformação de Legendre; o uso destes “truques” tornam a Termodinâmica algo abstrata, mas simultaneamente, muito poderosa.
² O resultado obtém-se diretamente da eq. (4): as derivadas cruzadas são iguais.

---

Recursos relacionados disponíveis na Casa das Ciências:

1. Capacidade Calorífica.
   

---

Criada em 5 de Junho de 2019
Revista em 5 de Junho de 2019
Aceite pelo editor em 21 de Junho de 2019