Referência : Lage, E., (2021) Campo magnético estacionário, Rev. Ciência Elem., V9(1):019
Autor: Eduardo Lage
Editor: José Ferreira Gomes
DOI: [https://doi.org/10.24927/rce2021.019]

---

[editar] Resumo

Correntes contínuas criam um campo magnético independente do tempo, sendo aqui deduzidas expressões gerais entre as fontes e o campo ilustradas por exemplos característicos e importantes, tais como espiras, solenóides e esferas carregadas em rotação uniforme. É introduzido o importante conceito de potencial vetorial magnético, um auxiliar no cálculo do campo magnético que permite obter a relação exata entre este e as correntes e que se reduz, em limites apropriados, à lei de Biot e Savart. Outro importante conceito é o momento magnético de uma distribuição de correntes, salientando- se que existem tais momentos de forma intrínseca para os quais se deduz o campo magnético por eles originado. A análise das forças que um campo magnético exerce sobre correntes é reservado para outro artigo.

O campo magnético estacionário é originado por correntes contínuas, não dependendo, pois, do tempo. Tal campo é regido pelo seguinte par das equações de Maxwell^[1]:

$\bigtriangledown \cdot \vec{B}=0$ (1)

$\bigtriangledown \cdot \vec{B}=\mu_{0}\vec{i}$ (2)

Comparando com as equações da Eletrostática^[2], conclui-se que a eq. (1) significa a inexistência de cargas magnéticas, pelo que as linhas de força do campo magnético são sempre fechadas. Pelo mesmo motivo, é contínua a componente normal do campo magnético através de qualquer superfície, mesmo que existam correntes superficiais.

A eq. (2), obtida primeiramente por Ampére, relaciona o campo com as correntes. É muito útil considerar a sua forma integral. Para isso, considere-se uma linha fechada $C$ onde se arbitra um sentido de circulação (FIGURA 1) – deste modo, fica definido, em cada ponto da linha, um vetor infinitesimal $d\vec{l}$, tangente à linha, com o sentido da circulação e grandeza $\left | d\vec{l} \right |$, o elemento de comprimento na linha. Designa-se por circulação do campo ao longo de $C$ o integral (soma) $\oint_{C}^{}d\vec{l}\cdot \vec{B}$. Seja, agora, uma qualquer superfície aberta a $\oint_{C}^{}d\vec{l}\cdot \vec{B}$ que se apoie em $C$.

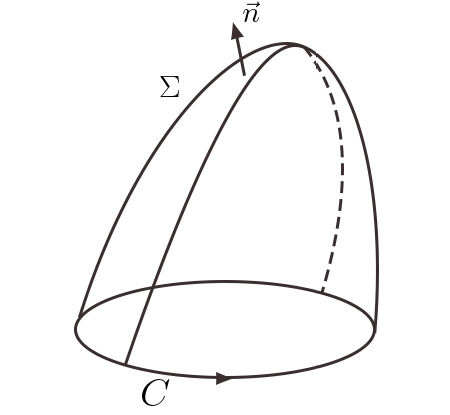
Em cada ponto desta superfície, fica definido o versor da normal $\vec{n}$ cujo sentido está relacionado com o sentido da circulação pela regra do saca-rolhas. Ora, pelo teorema de Stokes, tem-se^[3]:

$\oint_{C}^{}d\vec{l}\cdot \vec{B}=\int_{\Sigma_{a}}^{}dS\vec{n}\cdot \left ( \bigtriangledown \wedge \vec{B} \right )=\mu _{0}\int_{\Sigma_{a}}^{}dS\vec{n}\cdot \vec{i}\equiv \mu_{0}I$ (3)

onde $I$ é a intensidade da corrente que atravessa a superfície $\Sigma_{a}$ no sentido da normal definida. Esta eq. (3) é, muitas vezes, suficiente para determinar o campo magnético, como se mostra em alguns exemplos abaixo. Interessa, aqui, usá-la para estudar a descontinuidade da componente tangencial do campo através de superfícies onde existam correntes superficiais.

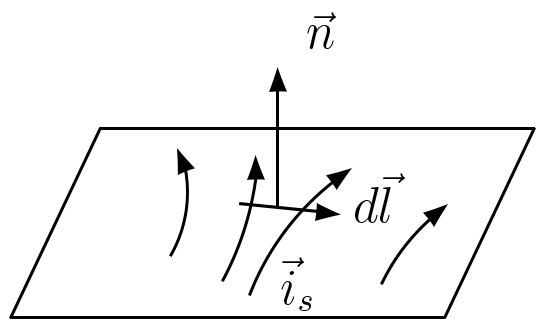
Tais correntes são uma idealização: qualquer corrente distribui-se, realmente, no espaço mas se estiver confinada a uma estreita vizinhança de uma superfície, é útil atribui-la inteiramente à superfície. Na FIGURA 2 considera-se uma tal superfície onde, num ponto qualquer, se define o versor da normal (de sentido arbitrário) e um pequeno vetor $d\vec{l}$ no plano tangente. Então, $\vec{i}_{s}\cdot \left ( \vec{n}\wedge d\vec{l} \right )$ é a intensidade da corrente que atravessa o comprimento $\left | d\vec{l} \right |$.

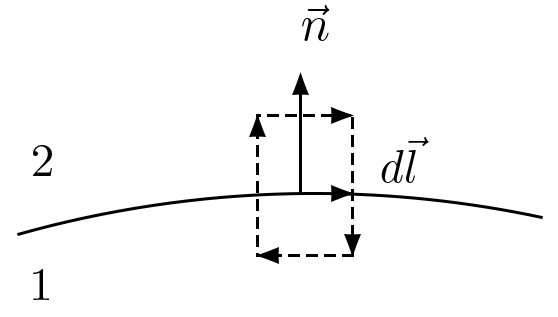
Construa-se, agora, um pequeno retângulo no plano determinado por $\vec{n}$ e $d\vec{l}$, e defina- -se o sentido de circulação (FIGURA 3). Seja $\vec{B}_{1}$ o campo abaixo do plano e $\vec{B}_{2}$ o campo acima do plano. Lembrando que a componente normal do campo é contínua, obtem-se pela eq. (3):

$\oint d\vec{l}\cdot\vec{B}=\left ( \vec{B}_{2}-\vec{B}_{1} \right )\cdot d\vec{l}=\mu_{0}\vec{i}_{s}\cdot\left ( \vec{n}\wedge d\vec{l} \right )=\mu_{0}\left ( \vec{i}_{s}\wedge \vec{n} \right )\cdot d\vec{l}$

Como o elemento $d\vec{l}$ é arbitrário na superfície, conclui-se:

$\vec{B}_{2}-\vec{B}_{1}=\mu_{0}\vec{i}_{s}\wedge\vec{n}\; \; \; \Leftrightarrow \; \; \; \vec{n}\wedge \left ( \vec{B}_{2}-\vec{B}_{1} \right )=\mu _{0}\vec{i}_{s}$ (4)

É esta a relação procurada para a descontinuidade das componentes tangenciais do campo.

Os exemplos seguintes ilustram a determinação do campo em várias situações de interesse.

Corrente uniforme em fio retilíneo

A FIGURA 4 representa um fio cilíndrico (raio $R$) de comprimento ilimitado percorrido por uma corrente de intensidade $I$. É útil usar coordenadas cilíndricas com o eixo $z$ coincidente com o eixo do cilindro. Considere-se um ponto $P$, interior ou exterior ao cilindro. O plano definido por este ponto e o eixo do cilindro é um plano de simetria por reflexão do sistema.

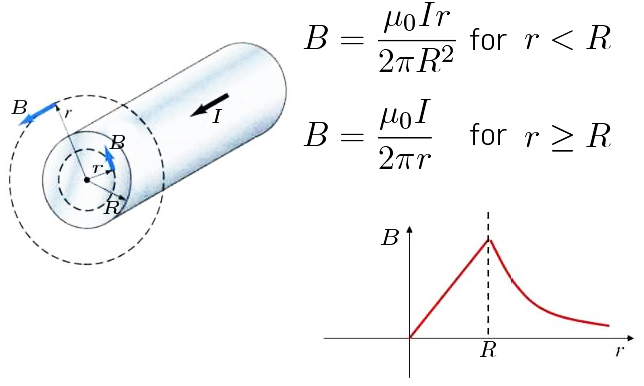
Ora, sendo $\vec{B}$ um pseudovetor, então, por reflexão neste plano, trocam de sinal as suas componentes paralelas ao plano e é invariante a sua componente $B_{\phi}$ perpendicular ao plano. Assim, é $B_{r}=B_{z}=0$. A simetria de rotação em torno do cilindro e a simetria de translação ao longo do cilindro indicam que é $B_{\phi}\left ( r \right )$. Seja, agora, uma circunferência (raio $r$) perpendicular ao eixo e nele centrada. Usando a eq. (3), tem-se:

$r>R\; \; \; B_{\phi}2\pi r=\mu_{0}I\; \; \; \rightarrow \; \; \; B_{\phi}=\frac{\mu_{0}I}{2\pi r}$

$r<\;R\; \; \; B_{\phi}2\pi r=\mu_{0}\frac{I}{\pi R^{2}}\pi r^{2}\; \; \; \rightarrow \; \; \; B_{\phi}=\mu_{0}I\frac{r}{R}$ (5)

Note-se que o campo é contínuo em R: não há correntes superficiais.

Corrente circular uniforme na superfície de um cilindro ilimitado

A FIGURA 5 representa um cilindro de comprimento ilimitado e secção reta circular (raio $a$). Na superfície do cilindro existe uma corrente superficial, circular e uniforme $\left ( \vec{i}_{s} \right )$.

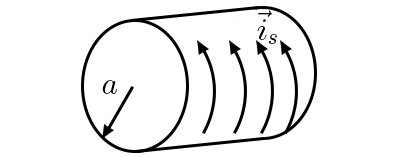
Tomando o eixo do cilindro para eixo $z$ de coordenadas cilíndricas, é imediato verificar que o pseudovetor $\vec{B}$ só tem não nula a componente $B_{z}$ devido à simetria de reflexão em qualquer plano normal ao eixo do cilindro. A simetria de rotação em torno deste eixo e a eq. (1) informam que só poderá ser $B_{z}(r)$; mas, no exterior do cilindro, sendo nulo o 2º membro da eq. (2), então $B_{z}$ terá de ser constante e esta tem de ser nula porque o campo deve anular-se longe do cilindro. Assim, $B_{z}$ está confinado ao interior do cilindro, onde não pode depender de $r$ pela eq. (2). Segue-se que $B_{z}$ é constante no interior do cilindro, obtendo-se, por aplicação da eq. (4):

$B_{z}=\mu_{0}i_{s}\; \; \; r<\;a$ (6)

Se o mesmo cilindro for percorrido por uma corrente superficial longitudinal (i.e. paralela ao eixo do cilindro), com a geometria da FIGURA 4, o campo é nulo no interior do cilindro e, no exterior, as suas linhas de força são circulares:

$B_{\phi}=0\; \; \; r<\;a$

$B_{\phi}=\mu_{0}i_{s}\frac{a}{r}\; \; \; r>a$ (7)

Estes dois resultados permitem-nos modelizar o campo gerado por um solenóide (FIGURA 6). O enrolamento ao longo do cilindro é helicoidal com um passo $h$, de modo que a equação da hélice é $z=h\frac{\phi}{2\pi}$, originando o versor da tangente (em coordenadas cilíndricas) $\vec{\tau }=\textrm{cos}\alpha \vec{e}_{\phi}+\textrm{sen}\vec{e}_{z}$, com $\textrm{cos}\alpha = \frac{\alpha }{\sqrt{a^{2}+\left ( \frac{h}{2\pi} \right )^{2}}}$.

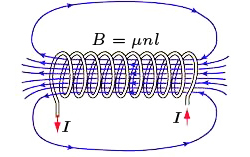
Deste modo, a densidade superficial de corrente fica $\vec{i}_{s}=i_{s}\vec{\tau }$. Considere-se um pequeno comprimento $\delta z$ de uma, qualquer, geratriz do cilindro. A corrente que passa através deste elemento é, por definição, $\vec{i}_{s}\cdot\vec{e}_{\phi}\delta z=i_{s}\textrm{cos}\alpha \delta z$. Por outro lado, há $n\delta z$ enrolamentos que atravessam aquele comprimento, onde $n$ é o número de enrolamentos por unidade de comprimento da geratriz. Cada enrolamento transporta a corrente de intensidade $I$, pelo que $i_{s}\textrm{cos}\alpha \delta z=In\delta z$, i.e., $i_{s}=\frac{nI}{\textrm{cos}\alpha }$, originando o respetivo vetor $\vec{i}_{s}=\frac{nI}{\textrm{cos}\alpha }\vec{\tau }=nI\vec{e}_{z}+nItg\alpha \vec{e}_{z}$. Esta corrente é, pois, a soma de uma corrente circular, perpendicular ao eixo do cilindro, $\vec{i}_{s}^{\perp }=nI\vec{e}_{\phi}$ com uma corrente longitudinal $\vec{i}_{s}^{\left | \right |}=nItg\alpha \vec{e}_{z}$, paralela àquele eixo. A primeira gera um campo no interior do cilindro (ver eq. (6)):

$B_{z}=\mu_{0}nI\; \; \; r<\;a$ (8)

A segunda gera um campo no exterior do cilindro (ver eq. (7):

$B_{\phi}=\mu_{0}nItg\alpha \frac{a}{r}=\mu_{0}nI\frac{h}{2\pi r}\; \; \; r>a$

Para um enrolamento muito apertado $\left ( h\ll a \right )$, este campo exterior é muito fraco e, na realidade, é dominado, para um solenóide de comprimento finito, pelo primeiro campo que fecha as suas linhas de força no exterior do cilindro (FIGURA 6).

O potencial vetor magnético

A eq. (1) é automaticamente satisfeitas se se escrever:

$\vec{B}=\bigtriangledown \wedge \vec{A}$ (9)

O potencial vetor magnético $\vec{A}$ é um vetor polar^[4] e a sua definição fica aqui completada com a escolha do padrão de Coulomb:

$\bigtriangledown \cdot\vec{A}=0$ (10)

Nestas condições, a equação de Maxwell-Ampére (eq. (2)) fica:

$\Delta \vec{A}=-\mu_{0}\vec{i}$ (11)

Comparando com a equação de Poisson da Eletrostática, é imediato concluir que a sua solução particular é:

$\vec{A}\left ( \vec{r} \right )=\frac{\mu_{0}}{4\pi}\int dV'\frac{\vec{i}\left ( \vec{r}' \right )}{\left | \vec{r}-\vec{r}' \right |}$ (12)

Esta expressão sugere, muitas vezes, que o potencial vetor magnético apresenta a mesma geometria das correntes, o que muito facilita a procura de soluções.

É fácil mostrar que satisfaz à condição (10) porque as correntes são estacionárias $\left ( \bigtriangledown \cdot\vec{i}=0 \right )$. O campo magnético obtém-se, agora, da eq. (9):

$\vec{B}\left ( \vec{r} \right )=\frac{\mu_{0}}{4\pi}\int dV'\bigtriangledown \left ( \frac{1}{\left | \vec{r}-\vec{r}' \right |} \right )\wedge \vec{i}\left ( \vec{r}' \right )=\frac{\mu_{0}}{4\pi}\int dV'\vec{i}\left ( \vec{r}' \right )\wedge \frac{\vec{r}-\vec{r}'}{\left | \vec{r}-\vec{r} \right |^{3}}$ (13)

Para correntes em fios finos, percorridos por uma corrente $I$ basta substituir $\int dV'\vec{i}\left ( \vec{r}' \right )\rightarrow Id\vec{l}$, obtendo-se assim a lei de Biot e Savart:

$\vec{B}\left ( \vec{r} \right )=\frac{\mu_{0}I}{4\pi}\oint d\vec{l}'\wedge \frac{\vec{r}-\vec{r}'}{\left | \vec{r}-\vec{r}' \right |^{3}}$ (14)

O integral faz-se ao longo do circuito onde $d\vec{l}'$ é um pequeno vetor, tangente em cada ponto ao circuito, com o sentido da corrente e grandeza igual ao elemento de comprimento. Deve observar-se que a eq. (14) perde validade na imediata vizinhança do fio condutor porque aí se faz sentir a espessura finita do fio, devendo então empregar-se a eq. (13) de validade genérica.

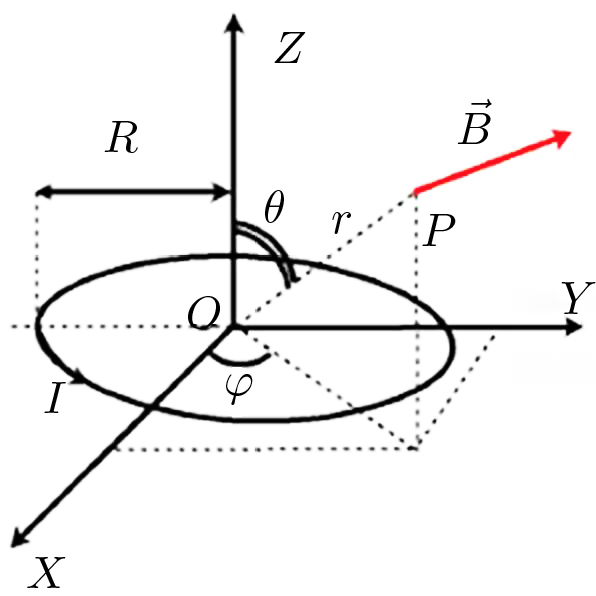
A FIGURA 7 representa uma espira circular (raio $R$) percorrida por uma corrente $I$. Pretende- se calcular o campo magnético a grandes distâncias da espira $\left ( r\gg R \right )$. A eq. (12) adaptada a esta geometria, fica:

$\vec{A}\left ( \vec{r} \right )=\frac{\mu_{0}I}{4\pi}\oint Rd\phi '\frac{\vec{e}_{\phi '}}{\left | \vec{r}-\vec{r}' \right |}\simeq \frac{\mu_{0}I}{4\pi}\frac{R}{r}\oint d\phi '\vec{e}_{\phi '}\left ( 1+\frac{\vec{r}\cdot \vec{r}}{r^{2}} \right )$

No último membro, o 1º termo é nulo; quanto ao seguinte, usando coordenadas esféricas com a origem no centro da espira e o eixo $z$ coincidente com o eixo da espira, tem-se (FIGURA 8):

$\vec{r}\cdot \vec{r}'=r\textrm{sen}\theta R\textrm{cos}\left ( \phi - \phi ' \right )$. Lembrando que $\vec{e}_{\phi '}=\left ( -\textrm{sen}\phi ',\textrm{cos}\phi ',0 \right )$ nos eixos cartesianos, obtem-se:

$\vec{A}\left ( \vec{r} \right )=\frac{\mu_{0}}{4\pi}I\textrm{sen}\left ( \theta \right )\frac{R^{2}}{r^{2}}\pi \vec{e}_{\phi}$

Donde (eq. (9)) o campo magnético:

$\frac{\vec{B}\left ( \vec{r} \right )}{\mu_{0}}=\frac{I\pi R^{2}}{4\pi r^{3}}\left ( 2\textrm{cos}\theta \vec{e}_{r}+\textrm{sen}\theta \vec{e}_{\theta} \right )$ (15)

A grandeza $I\pi R^{2}\equiv \mu$ é o momento magnético da espira, um importante conceito que se discutirá adiante.

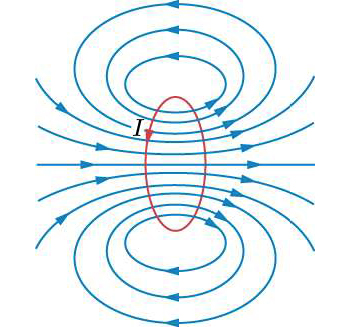
É interessante observar que se se empilharem idênticas espiras, o campo, no exterior deste conjunto, vai anular-se, ficando confinado ao seu interior e nas extremidades do empilhamento, tal como se encontrou no solenóide.

É, também, fácil calcular o campo ao longo do eixo da espira. A simetria de reflexão no plano da espira indica que apenas sobrevive a componente $B_{z}$ e, como o campo é um pseudo vetor, deve ser função par de $z$.

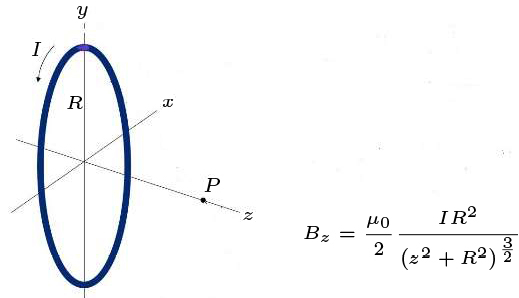
Usando a eq. (14), tem-se (FIGURA 9):

$\vec{B}=\frac{\mu_{0}}{4\pi}\frac{IR}{\left ( R^{2}+z^{2} \right )^{\frac{3}{2}}}\int_{0}^{2\pi}d\phi \left ( z\vec{e}_{r}' +R\vec{e}_{z} \right )=\frac{\mu_{0}}{2}\frac{IR^{2}}{\left ( R^{2}+z_{2} \right )^{\frac{3}{2}}}\vec{e}_{z}$

Um segundo exemplo considera uma distribuição uniforme de carga na superfície de uma esfera em rotação uniforme (velocidade angular $\omega$). Há, assim, uma densidade de corrente superficial:

$\vec{i}_{s}=\rho _{s}\vec{v}=\rho _{s}\vec{\omega }\wedge \vec{r}=\rho _{s}\omega R\textrm{sen}\theta \vec{e}_{\phi}$ (em coordenadas esféricas – FIGURA 10).

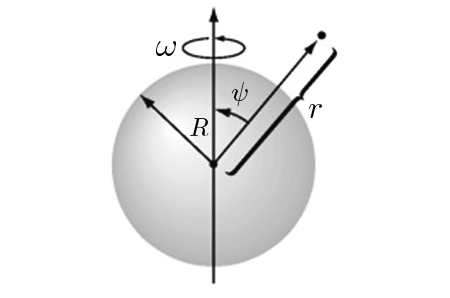
Tal sugere, juntamente com a simetria do problema, que o potencial vetor magnético tenha a forma $\vec{A}\left ( \vec{r} \right )=A\left ( r, \theta \right )\vec{e}_{\phi}$. Usando a eq. (9), obtem-se para o campo magnético:

$\frac{\vec{B}}{\mu_{0}}=\frac{1}{r\textrm{sen}\theta}\frac{\partial }{\partial \theta}\left ( \textrm{sen}\theta A \right )\vec{e}_{r}-\frac{1}{r}\frac{\partial }{\partial r}\left ( rA \right )\vec{e}_{\theta}$

Como $\bigtriangledown \wedge \vec{B}=0$ dentro e fora da esfera, tem-se:

$\frac{\partial ^{2}}{\partial r^{2}}\left ( rA \right )+\frac{1}{r\textrm{sen}\theta}\frac{\partial }{\partial \theta}\left ( \frac{1}{\textrm{sen}\theta}\frac{\partial }{\partial \theta}\left ( \textrm{sen}A \right ) \right )=0$

A expressão da densidade de corrente sugere a forma A(r, ) = f (r) sen . Substituindo, encontra-se:

$\frac{d^{2}}{dr^{2}}\left ( rf \right )-\frac{2}{r}f=0$

Esta equação tem as soluções $f\propto r$ e $f\propto \frac{1}{r^{2}}$. Assim, tem-se:

$r>R\; \; \; A\left ( \vec{r} \right )=\frac{C}{r^{2}}\textrm{sen}\theta\; \; \; \; \; \rightarrow \; \; \; \; \; \frac{\vec{B}}{\mu_{0}}=\frac{2C}{r^{3}}\textrm{cos}\theta \vec{e}_{r}+\frac{C}{r^{3}}\textrm{sen}\theta \vec{e}_{\theta}$

$r<\;R\; \; \; A\left ( \vec{r} \right )=Dr\textrm{sen}\theta\; \; \; \; \; \rightarrow \; \; \; \; \; \frac{\vec{B}}{\mu_{0}}=2D\textrm{cos}\theta \vec{e}_{r}+2D\textrm{sen}\theta \vec{e}_{\theta}=2D\vec{e}_{z}$

As constantes $C$ e $D$ são determinadas pelas condições na superfície da esfera:

- continuidade de $A\left ( R,\theta \right )\; \; \; \; \; \rightarrow \; \; \; \; \; \frac{C}{R^{3}}=D$

- descontinuidade de $B_{\theta}\left ( R,\theta \right )$ (eq. (4)) $\; \; \; \; \; \rightarrow \frac{C}{R^{3}}+2D=\rho _{s}\omega R$

Deste modo, o campo magnético fica:

$r>R\; \; \; \frac{\vec{B}}{\mu_{0}}=\frac{\rho _{s}\omega R^{4}}{3r^{3}}\left ( 2\textrm{cos}\theta \vec{e}_{r}+\textrm{sen}\vec{e}_{\theta} \right )$

$r<\;R\; \; \; \frac{\vec{B}}{\mu_{0}}=2\frac{\rho _{s}\omega R}{3}\textrm{cos}\theta\vec{e}_{r}-2\frac{\rho _{s}\omega R}{3}\textrm{sen}\theta\vec{e}_{\theta}=\frac{2\rho _{s}\omega R}{3}\vec{e}_{z}$

O campo no interior da esfera é uniforme, alinhando com o eixo de rotação. No exterior, comparando com a eq. (15), é o campo dipolar de um momento magnético de grandeza $\mu =\frac{4\pi}{3}\rho _{s}\omega R^{4}=\frac{1}{3}Q\omega R^{2}$, onde $Q$ é a carga da esfera (FIGURA 11).

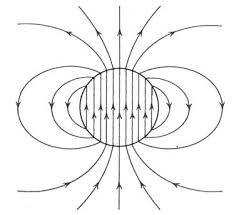
Este exemplo tem um certo valor histórico: quando foi descoberto o spin e se verificou que o eletrão tem um momento magnético intrínseco, procurou-se interpretar estes resultados com um modelo para o eletrão idêntico ao do exemplo. Contudo, Pauli objetou que, se assim fosse, com os valores conhecidos para aquelas grandezas e aceitando o raio clássico para o eletrão, então a velocidade da esfera no equador seria superior à velocidade da luz.

Se toda a esfera em rotação estiver carregada uniformemente e procedendo como atrás, mas havendo, agora, continuidade do campo na superfície, encontrar-se-ia:

$r\geq R\; \; \; \frac{B}{\mu_{0}}=\frac{\rho \omega R^{5}}{15r^{3}}\left [ 2\textrm{cos}\theta \vec{e}_{r}+\textrm{sen}\theta\vec{e}_{\theta} \right ]$

$r\leq R\; \; \; \frac{B}{\mu_{0}}=\rho \omega R^{2}\left [ \left ( \frac{1}{3}-\frac{r^{2}}{5R^{2}} \right )\textrm{cos}\theta\vec{e}_{r}-\left ( \frac{1}{3}-\frac{2r^{2}}{5R^{2}} \right )\textrm{sen}\theta\vec{e}_{\theta} \right ]$

Reconhece-se o campo dipolar no exterior da esfera.

O momento magnético

Para um sistema de correntes localizadas numa região finita do espaço (átomos, moléculas, etc.) o momento magnético é definido por:

$\vec{\mu}\equiv \frac{1}{2}\int dV\vec{r}\wedge \vec{i}$ (16)

É fácil mostrar que esta definição gera o resultado mais comum. Para um qualquer circuito elétrico, não necessariamente plano, tem-se:

$\vec{\mu}=\frac{I}{2}\oint \vec{r}\wedge d\vec{l}=I\vec{S}$ (17)

onde $\left | \vec{S} \right |$ é a área varrida pelo vetor de posição ao descrever o circuito e $I$ é a intensidade da corrente. Se este é plano, então $\vec{\mu}=IS\vec{n}$ (FIGURA 12), onde $\vec{n}$ é o versor da normal ao plano com o sentido definido pela circulação da corrente (regra do saca-rolhas).

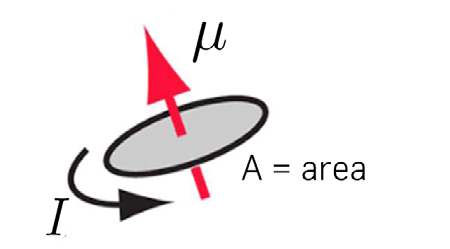
Considerem-se, agora, correntes de transporte $\left ( \vec{i}=\rho \vec{v} \right )$ e admita-se que os transportadores de carga (eletrões, iões) têm uma relação constante entre a sua carga e a sua massa (por exemplo, e $q_{e}/m_{e}$ para eletrões). Então, a razão entre as densidades de carga e massa $\left ( \frac{\rho }{\rho _{m}} \right )$ é constante. Assim, a eq. (16) fica:

$\vec{\mu}=\frac{1}{2}\int dV\vec{r}\wedge \left ( \rho \vec{v} \right )=\frac{\rho }{2\rho _{m}}dV\vec{r}\wedge \left ( \rho _{m}\vec{v} \right )=\frac{\rho }{2\rho _{m}}\vec{L}$

Aqui, $\vec{L}$ é o momento cinético orbital do sistema constituído pelas cargas. Para eletrões, é:

$\vec{\mu}=\frac{q_{e}}{2m_{e}}\vec{L}$

Na teoria de Bohr para o átomo de hidrogénio, a primeira órbita tem $L=\frac{h}{2\pi}$($h$ é a constante de Planck). O momento magnético associado é o magnetão de Bohr: $\mu_{B}=\frac{q_{e}}{2m_{e}}\frac{h}{2\pi}$. Designa-se por fator giromagnético orbital a razão entre o momento magnético (em unidades do magnetão de Bohr) e o momento cinético (em unidades de $\frac{h}{2\pi}$); para o eletrão, é $g_{o}=\frac{\left ( \frac{\mu}{\mu_{B}} \right )}{\frac{L}{\frac{h}{2\pi}}}=1$. Mas o eletrão também tem um momento cinético intrínseco – o spin – de valor $s=\frac{h}{4\pi}$ e um momento magnético intrínseco igual a um magnetão de Bohr. Assim, o fator giromagnético para o spin do eletrão é $g_{s}=2$. Para átomos ou iões, a respetiva estrutura eletrónica determina um arranjo quer dos momentos cinéticos quer dos momentos magnéticos que definem uma diversidade muito rica dos níveis energéticos, tal como inicialmente apresentada sob a forma de modelo vetorial do átomo. A diferença entre os fatores giromagnético e de spin determinam o fator giromagnético de Landé, a razão entre o momento magnético total (em unidades do magnetão de Bohr) e o momento cinético total (em unidades de $\frac{h}{2\pi}$) que explica quer o levantamento de degenerescências quer o comportamento do átomo ou ião sob acção de campos magnéticos aplicados. Não será prosseguido aqui este importante tópico.

Voltando ao momento magnético intrínseco do eletrão, a correspondente densidade de corrente escreve-se $\vec{i}=\bigtriangledown \wedge \vec{m}$, com $\vec{m}$ localizado no eletrão e satisfazendo a condição:

$\int dV\vec{m}=\vec{\mu}_{s}$ (18)

onde $\vec{\mu}_{s}$ é o momento magnético de spin. No Apêndice 1 é mostrado que esta densidade de corrente, inserida na eq. (16), faz identificar $\vec{\mu}=\vec{\mu}_{s}$.

Este resultado é importante pelo seguinte motivo. Em Eletrostática também se considerou o momento dipolar elétrico de um sistema de cargas^[5]. É um conceito útil porque permite obter o campo elétrico a grandes distâncias daquela distribuição, se esta tiver carga total nula. Mas se se aproximar da distribuição, o dipolo elétrico perde importância porque a distribuição fica resolvida como um conjunto de cargas – não existem dipolos elétricos elementares. Não é assim com o momento magnético do eletrão (e de outras partículas elementares): por muito que dele se se aproxime, aquele momento não fica resolvido como um sistema de correntes. É verdadeiramente uma propriedade do eletrão como ponto material (i.e., sem estrutura), tal como a sua carga elétrica ou a sua massa. É, por isso, importante, determinar o campo magnético gerado pelo momento magnético do eletrão.

Para isso, usando $\vec{i}=\bigtriangledown \wedge \vec{m}$ na eq. (2), tem-se:

$\bigtriangledown \wedge \left ( \frac{\vec{B}}{\mu_{0}}-\vec{m} \right )=0$

Definido:

$\vec{H}\equiv \frac{\vec{B}}{\mu_{0}}-\vec{m}$ (19)

este campo satisfaz às condições seguintes:

$\bigtriangledown \wedge \vec{H}=0\; \; \; \; \; \rightarrow \; \; \; \; \; \vec{H}=\bigtriangledown \psi$

$\bigtriangledown \cdot \vec{H}=-\bigtriangledown \cdot \vec{m}\; \; \; \; \; \rightarrow \; \; \; \; \; \Delta \psi =-\bigtriangledown \cdot \vec{m}$

A última equação é idêntica à equação de Poisson da Eletrostática, aparecendo $\bigtriangledown \cdot \vec{m}$ como uma “densidade de carga”. Aproveitando a solução aí encontrada, tem-se:

$\psi \left ( \vec{r} \right )=\frac{1}{4}\int dV'\frac{\bigtriangledown '\cdot \vec{m}\left ( \vec{r}' \right )}{\left | \vec{r}-\vec{r}' \right |}$

Aqui, $\bigtriangledown '$ é o operador gradiente que atua sobre as componentes de $\vec{r}'$. O integrando pode ser transformado pela identidade:

$\frac{\bigtriangledown '\cdot \vec{m}\left ( \vec{r}' \right )}{\left | \vec{r}-\vec{r}' \right |}=\bigtriangledown '\cdot \left [ \frac{\vec{m}\left ( \vec{r}' \right )}{\left | \vec{r}-\vec{r}' \right |} \right ]-\vec{m}\left ( \vec{r}' \right )\cdot \bigtriangledown '\left ( \frac{1}{\left | \vec{r}-\vec{r}' \right |} \right )$

O primeiro termo, inserido no integral, converte-se num fluxo (Gauss) através de uma superfície esférica de raio arbitrariamente grande, pelo que é nulo. Quanto ao segundo termo, atenta à identidade $\bigtriangledown '\left ( \frac{1}{\left | \vec{r}-\vec{r}' \right |} \right )=-\bigtriangledown \left ( \frac{1}{\left | \vec{r}-\vec{r}' \right |} \right )$, origina:

$\psi \left ( \vec{r} \right )=\frac{1}{4\pi}\bigtriangledown \cdot \int dV'\frac{\vec{m}\left ( \vec{r}' \right )}{\left | \vec{r}-\vec{r}' \right |}=\frac{1}{4\pi}\bigtriangledown \cdot\frac{\vec{\mu}_{s}}{\left | \vec{r}-\vec{r}_{1} \right |}=-\frac{1}{4\pi}\frac{\vec{\mu}_{s}\cdot \left ( \vec{r}-\vec{r}_{1} \right )}{\left | \vec{r}-\vec{r}_{1} \right |^{3}}$

porque $\vec{m}\left ( \vec{r} \right )$ está concentrado^[6] num ponto que, por escolha, se localiza em $\vec{r}_{1}$. A expressão final é muito semelhante ao potencial originado por um dipólo elétrico e, por isso, designa-se $\psi$ por potencial magnético (é, contudo, um pseudo-escalar). Deste modo, o campo $\vec{H}$ fica:

$\vec{H}\left ( \vec{r} \right )=\frac{1}{4\pi}\frac{3\vec{\mu}_{s}\cdot \left ( \vec{r}-\vec{r}_{1} \right )\left ( \vec{r}-\vec{r}_{1}-\vec{\mu}_{s}\left | \vec{r}-\vec{r}_{1} \right |^{2} \right )}{\left | \vec{r}-\vec{r}_{1} \right |^{5}}$ (20)

Reconhece-se este campo $\vec{H}$ em alguns dos exemplos anteriores. Finalmente, o campo magnético (eq. (19):

$\frac{\vec{B}\left ( \vec{r} \right )}{\mu_{0}}=\frac{1}{4\pi}\frac{3\vec{\mu}_{s}\cdot \left ( \vec{r}-\vec{r}_{1} \right )\left ( \vec{r}-\vec{r}_{1} \right )-\vec{\mu}_{s}\left | \vec{r}-\vec{r}_{1} \right |^{2}}{\left | \vec{r}-\vec{r}_{1} \right |^{5}}+\vec{m}\left ( \vec{r} \right )$ (21)

É, então, este o campo gerado por um momento magnético “pontual” – o último termo está, apenas, localizado no ponto $\vec{r}_{1}$. É nulo para $\vec{r}\neq \vec{r}_{1}$, mas a sua importância não pode ser desprezada pois manifesta-se na origem da risca de 21 cm que caracteriza o espectro do hidrogénio em Cosmologia.

Será evidente que, para uma coleção de momentos magnéticos intrínsecos, o campo magnético é a soma dos campos originados por cada um.

Um importante resultado, demonstrado no Apêndice 2, considera um sistema de correntes confinadas a uma região finita do espaço e que, portanto, satisfaz:

$\int dV\vec{i}\left ( \vec{r} \right )=0$ (22)

Então, o momento magnético definido para tais correntes (eq. (16)) obedece à relação:

$\vec{\mu}=\int dV\frac{\vec{B}\left ( \vec{r} \right )}{\mu_{0}}+\frac{1}{2}\int dS\vec{r}\wedge \left ( \vec{n}\wedge \frac{\vec{B}\left ( \vec{r} \right )}{\mu_{0}} \right )$ (23)

O primeiro integral é estendido a todo o espaço e o segundo refere-se a uma superfície esférica de raio arbitrariamente grande ($\vec{n}$ é o versor da normal exterior). É fácil, embora trabalhoso, verificar que o resultado expresso pela eq. (21) satisfaz a relação anterior, sendo essencial a presença do último termo naquela equação.

A expansão multipolar

Partindo da eq. (12), considerando as correntes localizadas numa região finita do espaço, escolha-se um ponto de observação bem afastado das correntes. Tem-se:

$\vec{A}\left ( \vec{r} \right )=\frac{\mu_{0}}{4\pi r}\int dV'\vec{i}\left ( \vec{r}' \right )\left [ 1+\frac{\vec{r}\cdot \vec{r}'}{r^{2}}+... \right ]$

Os termos ignorados definem momentos quadrupolares, etc. O integral do primeiro termo é nulo. Quanto ao segundo, usem-se os resultados obtidos no Apêndice 2, para obter (exemplifica-se com a componente segundo $x_{1}$):

$A_{1}\left ( \vec{r} \right )=\frac{\mu_{0}}{4\pi r^{3}}\int dV'i_{1}\left ( \vec{r}' \right )\vec{r}'\cdot \vec{r}=\frac{\mu_{0}}{4\pi r^{3}}\int dV'i_{1}\left ( \vec{r}' \right )\left ( x_{1}^{'}x_{2}+x_{3}x_{3} \right )=$

$=\frac{\mu_{0}}{4\pi r^{3}}\left ( -x_{2}\mu_{3}+x_{3}\mu_{2} \right )=\frac{\mu_{0}}{4\pi r^{3}}\left ( \vec{\mu}\wedge \vec{r} \right )_{1}$

$=\frac{\mu_{0}}{4\pi r^{3}}\left ( -x_{2}\mu_{3}+x_{3}\mu_{2} \right )=\frac{\mu_{0}}{4\pi r^{3}}\left ( \vec{\mu}\wedge \vec{r} \right )_{1}$

Com idêntico procedimento para as outras componentes, tem-se finalmente:

$\vec{A}\left ( \vec{r} \right )=\frac{\mu_{0}}{4\pi r^{3}}\vec{\mu}\wedge \vec{r}$ (24)

Donde:

$\frac{\vec{B}}{\mu_{0}}=\bigtriangledown \wedge \frac{\vec{A}}{\mu_{0}}=\frac{1}{4\pi}\left ( \frac{3\left ( \vec{\mu}\cdot\vec{r} \right )\vec{r}-\vec{\mu}r^{2}}{r^{5}} \right )$

É o campo de um dipólo magnético (ver eq. (20)). Deste modo, a grandes distâncias de correntes localizadas (átomos, moléculas, espiras, etc.), o campo magnético é o do dipólo magnético associado ao sistema de correntes.

A Terra possui um campo magnético que, à superfície, tem uma intensidade entre 25 e 65 $\mu T$ (1 tesla=1Wb/m²=10⁴ gauss), estimando-se, assim, $H\sim \frac{650}{4\pi}A/M$ no pólo norte magnético (que é, aproximadamente, o pólo sul geográfico). Tal corresponde a um momento magnético localizado no centro da Terra ($R\sim 6400$ km ) de grandeza $\mu \sim 65 \times 10^{12}Am^{2}$. O campo magnético no exterior da Terra deflecte partículas carregadas (raios cósmicos, vento solar) para os pólos magnéticos onde interagem com a alta atmosfera criando auroras boreais. Neste artigo foram apenas consideradas propriedades genéricas do campo magnético estacionário. Ora, tal campo manifesta-se através de forças que exerce sobre correntes, realizando trabalho e conduzindo à identificação de uma energia magnética. Estes são importantes tópicos a considerar noutro artigo.

Apêndice 1 - Demostração de $\vec{\mu}_{s}$, definido na eq. (18), ser um momento magnético.

Com efeito, usando $\vec{i}=\bigtriangledown \wedge \vec{m}$ na eq. (16), tem-se:

$\vec{\mu}=\frac{1}{2}\int dV\vec{r}\wedge \left ( \bigtriangledown \wedge \vec{m} \right )=\frac{1}{2}\int dV\left [ \bigtriangledown _{\vec{m}}\left ( \vec{r}\cdot\vec{m} \right )-\vec{r}\cdot \bigtriangledown \vec{m} \right ]$

onde $\bigtriangledown_\vec{m}$ significa que o operador gradiente só atua sobre $\vec{m}$. Ora, $\bigtriangledown _{\vec{m}}\left ( \vec{r}\cdot \vec{m} \right )=\bigtriangledown \left ( \vec{r}\cdot \vec{m} \right )-\bigtriangledown _{\vec{r}}\left ( \vec{r}\cdot \vec{m} \right )=\bigtriangledown \left ( \vec{r}\cdot\vec{m} \right )-\vec{m}$ , inserido no integral inicial, converte-se (teorema de Gauss) num fluxo sobre uma superfície esférica de raio arbitrariamente grande onde $\vec{m}$ é nulo, pelo que é nula tal contribuição. Quanto ao (pseudo) vetor $\vec{r}\cdot \bigtriangledown \vec{m}$, considere-se uma sua componente genérica: $\vec{r}\cdot\bigtriangledown m_{i}=\sum_{j}^{}x_{j}\frac{\partial m_{i}}{\partial x_{j}}=\sum_{j}^{}\frac{\partial \left ( x_{j}m_{i} \right )}{\partial x_{j}}-3m_{i}$. Inserindo no integral, o primeiro termo desta expressão anula-se pelo motivo anterior. Assim, o integral fica $\frac{1}{2}\int dV\left [ \bigtriangledown _{m}\left ( \vec{r}\cdot \vec{m} \right ) -\vec{r}\cdot\bigtriangledown \vec{m} \right ]=\frac{1}{2}\int dV\left ( -\vec{m}+3\vec{m} \right )=\int dV\vec{m}=\vec{\mu}_{s}$ confirmando a identificação de $\vec{\mu}_{s}$ como momento magnético.

Apêndice 2 - Demonstração da eq. (23)

Considere-se o integral $\int dVx_{k}\vec{i}\left ( \vec{r} \right )$, onde $x_{k}$ é uma componente genérica do vetor de posição. Utilizando a eq. (2), tem-se:

$\int dVx_{k}\vec{i}\left ( \vec{r} \right )=\int dVx_{k}\bigtriangledown \wedge \frac{\vec{B}}{\mu_{0}}=\int dV\left [ \bigtriangledown \wedge \left ( \frac{x_{k}\vec{B}}{\mu_{0}} \right )-\vec{e}_{k}\wedge \frac{\vec{B}}{\mu_{0}} \right ]=\int_{\Sigma}^{}dS\left ( \vec{n}\wedge \frac{\vec{B}}{\mu_{0}} \right )x_{k}-\int dV\vec{e}_{k}\wedge \frac{\vec{B}}{\mu_{0}}$

Aqui, usou-se o teorema de Gauss para converter o primeiro termo num integral sobre uma superfície (esférica), de normal exterior $\vec{n}$ e de raio arbitrariamente grande, no interior da qual se localizam as correntes. Projectando no eixo cartesiano $x_{j}$, obtem-se:

$\int dVx_{k}i_{j}\left ( \vec{r} \right )=-\int dV\vec{e}_{k}\wedge \frac{\vec{B}}{\mu_{0}}\cdot \vec{e}_{j}+\int_{\Sigma}^{}dS\left ( \vec{n}\wedge \frac{\vec{B}}{\mu_{0}} \right )x_{k}=$

$=\int dV\vec{e}_{j}\wedge \vec{e}_{k}\cdot\frac{\vec{B}}{\mu_{0}}+\int_{\Sigma}^{}dS\left ( \vec{n}\wedge \frac{\vec{B}}{\mu_{0}} \right )x_{k}$ (25)

Donde:

$\frac{1}{2}\int dV\left [ x_{k}i_{j}\left ( \vec{r} \right )-x_{j}i_{k}\left ( \vec{r} \right ) \right ]=\int dV\vec{e}_{j}\wedge \vec{e}_{k}\cdot\frac{\vec{B}}{\mu_{0}}+\frac{1}{2}\int_{\Sigma}^{}dS\left [ \left ( \vec{n}\wedge \frac{\vec{B}}{\mu_{0}} \right )x_{k}-\left ( \vec{n}\wedge \frac{\vec{B}}{\mu_{0}} \right )x_{j} \right ]$

Considere-se, por exemplo, $k=1$ e $j=2$. Atendendo à definição de momento magnético (eq. (16)), vem:

$\mu_{3}=\int dV\frac{B_{3}}{\mu_{0}}+\frac{1}{2}\int_{\Sigma}^{}dS\left [ \vec{r} \wedge \left ( \vec{n}\wedge \frac{\vec{B}}{\mu_{0}} \right )\right ]_{3}$

Idênticos procedimentos para as outras duas escolhas independentes dos índices $k$ e $j$, resultam na eq. (23).

Regressando à eq. (25), considerem-se agora os elementos diagonais, por exemplo, $k=j=1$. Tem-se:

$\int dVx_{1}i_{1}\left ( \vec{r} \right )=\int_{\Sigma}^{}dS\left ( \vec{n}\wedge \frac{\vec{B}}{\mu_{0}} \right )_{1}x_{1}$

Aceitando $\Sigma$ como uma superfície esférica de raio $R\rightarrow \infty$, o 2º membro fica:

$R^{3}\int_{\Sigma}^{}d\Omega \left ( \vec{n}\wedge \frac{\vec{B}}{\mu_{0}} \right )_{1}n_{1}$

O integral é, agora, efectuado sobre as direções definidas pelo ângulo sólido. Este termo é nulo se o campo decair mais rapidamente do que $1/R^{3}$. E mesmo para um dipólo magnético, deduz-se da eq. (20) que este termo se reduz a:

$-\frac{1}{4}\int_{\Sigma}^{}d\Omega \left ( \vec{n}\wedge \vec{\mu} \right )_{1}n_{1}=0$

como resulta da integração angular para $n_{1}n_{2}$ e $n_{1}n_{3}$. Assim, tem-se:

$\int dVx_{1}i_{1}\left ( \vec{r} \right )=0$

[editar] Referências

1. ↑ LAGE, E., Os fundamentos do eletromagnetismo, Rev. Ciência Elem., V9(1):016. (2021). DOI: 10.24927/rce2021.016.
2. ↑ LAGE, E., Eletrostática, Rev. Ciência Elem., V9(1):015. (2021). DOI: 10.24927/rce2021.015.
3. ↑ LAGE, E., Gradiente, divergência e rotacional, Rev. Ciência Elem., V8(2):029. (2020). DOI: 10.24927/rce2020.029.
4. ↑ LAGE, E., Os fundamentos do eletromagnetismo, Rev. Ciência Elem., V9(1):016. (2021). DOI: 10.24927/rce2021.016.
5. ↑ LAGE, E., Eletrostática, Rev. Ciência Elem., V9(1):015. (2021). DOI: 10.24927/rce2021.015.
6. ↑ LAGE, E., Eletrostática, Rev. Ciência Elem., V9(1):015. (2021). DOI: 10.24927/rce2021.015.

---

Criada em 11 de Abril de 2020
Revista em 27 de Janeiro de 2021
Aceite pelo editor em 31 de Março de 2021