Baricentro

Referência : Amaral, V., Lopes, A., Ralha, M.E., Taveira, C., Sousa, I., (2014) Baricentro, Rev. Ciência Elem., V2(3):212
Autores: V. Amaral, A. Lopes, E. Ralha, I. Sousa, C. Taveira
Editor: José Francisco Rodrigues
DOI: [http://doi.org/10.24927/rce2014.212]

---

Este conceito aparece em vários contextos, na geometria, na estatística e em Física associado a Centro de massa

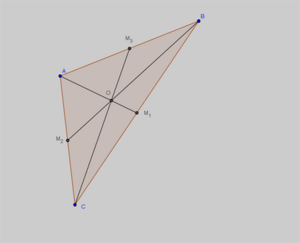
Baricentro, de um triângulo.

Baricentro de um triângulo é o ponto de interseção das suas medianas.

Notas e Exemplos

Verifique a posição relativa das medianas e do baricentro - $I$ - para diferentes triângulos, deslocando os vértices $A$, $B$ e/ou $C$.

TEOREMA: A distância do baricentro a qualquer vértice do triângulo a que pertence é igual a $\frac{2}{3}$ do comprimento da respetiva mediana.

Na figura anterior tem-se que:

$$\overline{OA}=\frac{2}{3}\overline{AM_1},$$ $$\overline{OB}=\frac{2}{3}\overline{BM_2},$$ $$\overline{OC}=\frac{2}{3}\overline{CM_3}$$

Baricentro, em Estatística.

Baricentro é, num contexto de Estatística e num plano, o centro de um conjunto de pontos, que constituem uma amostra de dados bivariados.

Notas

O baricentro não tem que fazer necessariamente parte da amostra.

Considerando a amostra de dados bivariados $x_i,y_i$, $i =1,...,n$, o baricentro dessa amostra é o ponto de coordenadas $(\bar{x},\bar{y})$,com $\bar{x}$ e $\bar{y}$ as médias dos valores $x_i$ e $y_i$), respetivamente.

Exemplo

Considerando a amostra bivariada:

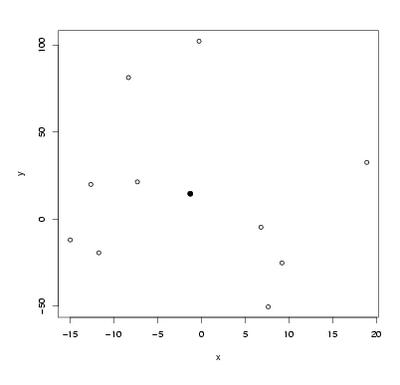
$x$	-7.31	-12.63	-11.71	18.92	-0.26	6.82	7.65	-8.33	-14.99	9.22	$\bar{x} = -1.262$
$y$	21.43	19.98	-19.32	32.62	102.27	-4.61	-50.34	81.37	-11.93	-25.11	$\bar{y}= 14.636$

o baricentro é o ponto de coordenadas $(-1.262,14.636)$, representado no gráfico da imagem 1 pelo ponto a cheio.

---

Criada em 17 de Junho de 2011
Revista em 25 de Maio de 2012
Aceite pelo editor em 05 de Junho de 2012