As equações de Fresnel
Referência : Lage, E., (2023) As equações de Fresnel, Rev. Ciência Elem., V11(3):029
Autora: Eduardo Lage
Editor: João Nuno Tavares
DOI: [https://doi.org/10.24927/rce2023.029]

[editar] Resumo
As leis da ótica geométrica são completamente reproduzidas pelas condições cinemáticas do eletromagnetismo para ondas que incidam sobre uma superfície que divide dois meios distintos. Mas o eletromagnetismo vai mais longe porque fornece expressões bem definidas para as amplitudes relativas das ondas refletida e transmitida– são a equações de Fresnel (1823). Com base nelas, são estudadas a refletância e transmitância para diversos tipos de interfaces separando meios lineares, isotrópicos e não magnéticos, introduz-se o ângulo de Brewster e considera-se a pressão que a radiação exerce sobre um bom condutor.
Quando uma onda eletromagnética incide na superfície plana que separa dois meios diferentes, são originadas uma onda refletida e uma onda transmitida. Para uma onda incidente plana e monocromática, toda a dependência dos seus campos no espaço e no tempo é definida pelo fator:
\(e^{i\left ( \vec{k}\cdot\vec{r}-\omega t \right )}\) (1)
onde \(\vec{k}\) é o vetor de onda e \(\omega\) a frequência angular. As condições de passagem no plano de separação (que se tomará para plano \(xz\), com o eixo \(y\) perpendicular), são relações lineares entre componentes do campo e determinam que as três ondas têm a mesma frequência e a mesma componente do vetor de onda naquele plano[1]:
\(k_{x}^{\left ( i \right )}=k_{x}^{\left ( r \right )}=k_{x}^{\left ( t \right )}\) (2)
Conhecidas as relações de dispersão[2] em cada meio, ficam completamente determinados os vetores de onda. Em particular, para a onda refletida, propagando-se no mesmo meio da incidente, a equação (2) impõe:
\(k_{y}^{\left ( r \right )}=-k_{y}^{\left ( i \right )}\) (3)
Isto é, o ângulo de incidência é igual ao ângulo de reflexão.
Admitir-se-á doravante que o meio onde se propaga a onda incidente é um dielétrico transparente (identificado por meio 1); quanto ao outro meio (meio 2), tanto pode ser outro dielétrico transparente como um condutor. Aceitando que nenhum dos meios é magnético, a relação de dispersão[3] é, genericamente:
\(\vec{k}^2=\frac{\omega^2}{c^2}\left ( \varepsilon _r+i\frac{\sigma }{\omega\varepsilon _0} \right )\) (4)
onde \(\varepsilon _r\) e \(\sigma\) são, respectivamente, a permitividade relativa e a condutividade do meio, uma e outra dependentes da frequência.
Os dielétricos são, em geral, isoladores \(\left ( \sigma=0 \right )\), o que conduz à identificação do seu índice de refração:
\(\eta=\sqrt{\varepsilon _r}\) (5)
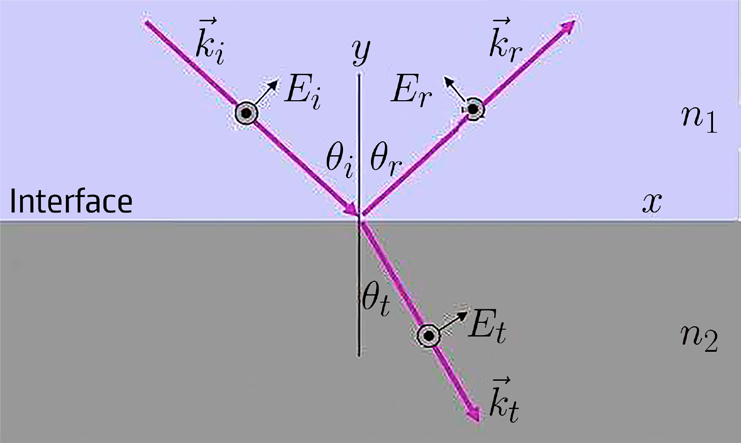
Esta identificação justifica-se porque, para dois dielétricos em presença, a equação (2) origina a lei de Snell (FIGURA 1):
\(\eta_1\textrm{sen}\theta_i=\eta_2\textrm{sen}\theta_t\) (6)
Para bons condutores \(\left ( \sigma\approx 10^7\Omega ^{-1}m^{-1} \right )\) e para frequências óticas \(\left ( \nu \equiv \frac{\omega}{2\pi}10^{14}s^{-1} \right )\) o termo \(\frac{\sigma}{\omega\varepsilon _0}\sim 10^4\) na equação (4), pelo que pode ignorar-se a permitividade relativa, \(\varepsilon _r\sim 1\). A onda transmitida é fortemente atenuada.
Neste artigo são deduzidas as relações entre as amplitudes dos campos e discutidas em detalhe as suas consequências para as duas naturezas limite do segundo meio. Estas relações são conhecidas por equações de Fresnel. Recorda-se que as ondas são transversais para meios lineares isotrópicos e que os campos elétrico, \(\vec{E}\), e magnético, \(\vec{H}\), satisfazem, genericamente, em cada meio, as seguintes equações:
\(\vec{k}\wedge \vec{E}=\mu_0\omega\vec{H}\) (7)
\(\vec{k}\wedge \vec{H}=\omega\varepsilon _0\left ( \varepsilon _r+i\frac{\sigma}{\omega\varepsilon _0} \right )\vec{E}\) (8)
com \(\varepsilon _0\mu_0c^2=1\) (\(c\) é a velocidade da luz no vazio).
Na superfície de separação, as relações de passagem, para além das equações (2), exigem a continuidade do campo magnético e da componente tangencial do campo elétrico, mas, como se verá, só há duas independentes.
Seja qual for o estado de polarização da onda incidente, é sempre possível considerar o seu campo elétrico como sobreposição de duas componentes, uma paralela ao plano de incidência e a outra perpendicular. Estes dois casos são tratados separadamente no que se segue.
Componentes paralelas.
A FIGURA 1 mostra as componentes paralelas do campo elétrico, também se identificando as componentes (perpendiculares) do campo magnético, dirigidas para cá (círculos negros), pelo que são nulas as suas componentes normais à superfície de separação (plano \(xz\)). Quanto à continuidade das componentes tangenciais do campo magnético, tem-se, pela equação (7):
\(k^{\left ( i \right )}\left ( E_i+E_r \right )=k^{\left ( t \right )}E_t\) (9)
onde:
\(k^{\left ( i \right )}=\frac{\omega}{c}\eta_1\) (10)
é a grandeza do vetor de onda comum para as ondas incidente e refletida.
A continuidade da componente tangencial do campo elétrico dá:
\(\left ( E_i-E_r \right )\cos\theta_i=E_t\cos\theta_t\) (11)
É óbvio que as componentes normais do deslocamento elétrico, \(\vec{D}\), são nulas pelo que é nula a densidade superficial de carga livre.
a) Admitindo que o meio 2 é, também, um dielétrico, então:
\(k^{\left ( t \right )}=\frac{\omega}{c}\eta_2\) (12)
Assim, das equações (9) e (11) resultam as razões:
\(r_{\parallel }\equiv \frac{E_r}{E_i}=\frac{\eta_2\cos\theta_i-\eta_1\cos\theta_t}{\eta_2\cos\theta_i+\eta_1\cos\theta_t}=\frac{\textrm{sen}\left ( 2\theta_i \right )-\textrm{sen}\left ( 2\theta_t \right )}{\textrm{sen}\left ( 2\theta_i \right )+\textrm{sen}\left ( 2\theta_t \right )}\)
\(t_{\parallel }\equiv \frac{E_t}{E_i}=\frac{\textrm{sen}\theta_i\cos\theta_i}{\eta_2\cos\theta_i+\eta_1\cos\theta_t}=\frac{2\textrm{sen}\theta_t\cos\theta_i}{\textrm{sen}\left ( 2\theta_i \right )+\textrm{sen}\left ( 2\theta_t \right )}\) (13)
Aqui, as últimas expressões obtiveram-se invocando a lei de Snell. Estes resultados são conhecidos por equações de Fresnel para as componentes paralelas.
Para incidência normal, tem-se simplesmente:
\(r_{\parallel }=\frac{\eta_2-\eta_1}{\eta_2+\eta_1}\; \; \; \; \; t_{\parallel }=\frac{2\eta_1}{\eta_2+\eta_1}\) (14)
Observando a expressão de \(r_{\parallel }\) na equação (13), conclui-se que esta razão se anula quando \(\theta_i+\theta_t=\frac{\pi}{2}\).
Tal ângulo de incidência é designado por ângulo de Brewster (1815), \(\theta_B\). Usando a lei de Snell, obtém-se:
\(\textrm{tg}\left ( \theta_B \right )=\frac{\eta_2}{\eta_1}\) (15)
Tem-se \(\theta_B\approx 53\)° para a água e \(\theta_B\approx 56\)° para o vidro.
A discussão seguinte distingue os casos \(\eta_1<\eta_2\) e \(\eta_1>\eta_2\).
- Para \(\eta_1<\eta_2\), por exemplo, interface ar ou vazio \(\left ( \eta=1 \right )\) e água \(\left ( \eta=\frac{4}{3} \right )\) ou vidro \(\left ( \eta=\frac{3}{2} \right )\), a lei de Snell mostra que é sempre \(\theta_t<\theta_i\) pelo que as equações (13) são reais.
- Para \(\eta_1>\eta_2\), por exemplo, trocando os meios anteriores, existe um ângulo (de incidência) limite, \(\theta_L\) para o qual é \(\theta_t=\frac{\pi}{2}\). Invocando a lei de Snell, tem-se \(\textrm{sen}\left ( \theta_L \right )=\frac{\eta_2}{\eta_1}\) (note-se: \(\theta_L>\theta_B\)).
i) Para \(\theta_i\leq \theta_L\) as equações 13 aplicam-se tal como estão escritas, verificando-se que, no ângulo limite, é \(r_{\parallel }=1\) e \(t_{\parallel }=\frac{\eta_1}{\eta_2}\).
ii) Para \(\theta>\theta_L\) a lei de Snell conduz a um ângulo \(\theta_L\) complexo, o que apenas significa que não pode mais ser interpretado geometricamente, apenas havendo necessidade de interpretar os resultados já obtidos. Na verdade, convém lembrar que \(k^{\left ( t \right )}\cos\theta_t\equiv k_{y}^{\left ( t \right )}\) sendo fácil obter esta grandeza através da lei de dispersão:
\(k_{y}^{\left ( t \right )}\equiv k^{\left ( t \right )}\cos\theta_t=\sqrt{k^{\left ( t \right )2}-\left ( k^{\left ( i \right )}\textrm{sen}\theta_i \right )^2}=\frac{\omega}{c}\sqrt{\eta_{2}^{2}-\left ( \eta_1\textrm{sen}\theta_i \right )^2}=-i\frac{\omega}{c}\eta_1\sqrt{\left ( \textrm{sen}\theta_i \right )^2-\left ( \textrm{sen}\theta_L \right )^2}\)
O sinal é escolhido de modo a garantir que a onda transmitida atenua dentro do meio 2 (onde é \(y\) < \(0\)) como decorre da equação (1). Assim:
\(\cos\theta_t=-i\frac{\eta_1}{\eta_2}\sqrt{\left ( \textrm{sen}\theta_i \right )^2-\left ( \textrm{sen}\theta_L \right )^2}=-i\sqrt{\left ( \frac{\textrm{sen}\theta_i}{\textrm{sen}\theta_L} \right )^2-1}\) (16)
A atenuação da onda transmitida não se deve a qualquer processo dissipativo, como se mostrará a seguir. Usando o resultado anterior nas equações (13), conclui-se ser \(\left | r_\parallel \right |=1\).
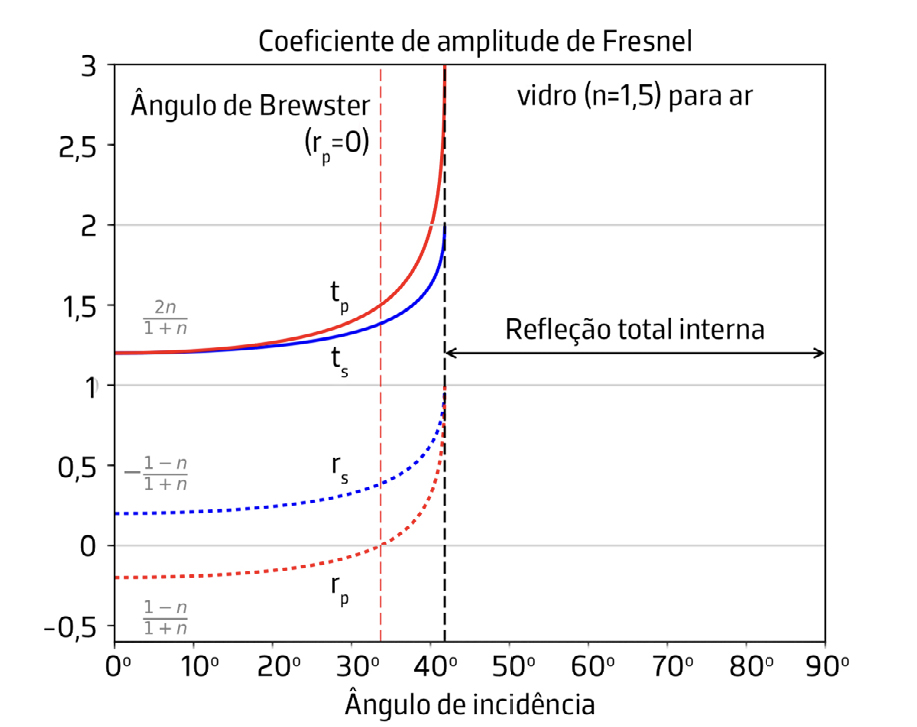
As amplitudes relativas para as ondas refletida e transmitida estão representadas nas FIGURAS 4 e 6.
b) Considere-se agora o caso de o meio 2 ser um bom condutor onde incide luz visível de modo que \(\frac{\sigma}{\omega\varepsilon _0}\gg 1\). Nestas condições, a relação de dispersão para este meio fica:
\(k^{\left ( t \right )2}\simeq \frac{\omega^2}{c^2}\left ( i\frac{\sigma}{\omega\varepsilon _0} \right )\; \; \; \; \; \rightarrow \; \; \; \; \; \frac{k^{\left ( i \right )}}{\left | k^{\left ( t \right )} \right |}\simeq \frac{\eta_1}{\left ( \frac{\sigma}{\omega\varepsilon _0} \right )}\ll 1\) (17)
Da lei de Snell tira-se:
\(\textrm{sen}\theta_t=\frac{k^{\left ( i \right )}}{k^{\left ( t \right )}}\textrm{sen}\theta_i\; \; \; \; \; \rightarrow \; \; \; \; \; \; \theta_t\simeq \frac{k^{\left ( i \right )}}{k^{\left ( t \right )}}\textrm{sen}\theta_i\) (18)
Deste modo, a componente:
\(\left [ \vec{k}^{\left ( t \right )} \right ]_y=-k^{\left ( t \right )}\cos\theta_t\simeq -k^{\left ( t \right )}=-\left ( 1+i \right )\frac{\omega}{c}\sqrt{\frac{\sigma}{2\omega\varepsilon _0}}\) (19)
onde o sinal da parte imaginária é escolhido para caracterizar o amortecimento da onda transmitida no meio 2 (onde é \(y\) < \(0\), ver equação 1). Note-se que a amplitude da onda decresce exponencialmente, podendo considerar-se nula para uma distância \(\delta \sim \frac{c}{\omega}\sqrt{\frac{2\omega\varepsilon _0}{\sigma}}\approx \frac{\lambda^{\left ( i \right )}}{2\pi}\sqrt{\frac{2\omega\varepsilon _0}{\sigma}}\ll \lambda^{\left ( i \right )}\)), independente do ângulo de incidência: \(\delta\) é o comprimento de penetração. Este amortecimento é, evidentemente, devido a efeito Joule, sendo da nossa experiência comum sentir um metal quente quando exposto à luz solar. Se o meio 2 for uma fina lamina do condutor (espessura \(<\delta\)), a lamina actua como um filtro redutor da luz incidente, um efeito utilizado nas viseiras de astronautas.
Das relações de Fresnel, obtém-se agora:
\(r_\parallel \approx 1\)
\(t_\parallel \approx 1\frac{2k^{\left ( i \right )}}{k^{\left ( t \right )}}\) (20)
A onda refletida transporta, praticamente, toda a energia da onda incidente, como a seguir se mostra.
Fluxos de energia.
O vetor de Poynting:
\(\vec{S}=\vec{E}\wedge \vec{H}\) (21)
determina o fluxo de energia através de qualquer superfície. Interessa aqui considerar apenas o plano \(\left ( y=0 \right )\) que separa os dois meios em presença e onde são iguais as fases \(k_xx-\omega t\) para as três ondas. É habitual considerar a média no tempo (sobre um período de oscilação) do vetor de Poynting, de modo que o fluxo incidente, para qualquer dos meios, no plano, é:
\(I=\left \langle \vec{S} \right \rangle\cdot\left ( -\vec{e}_y \right )=-\left \langle S_y \right \rangle=-\frac{1}{2}\textrm{Re}\left [ \vec{E}^*\wedge \vec{H} \right ]_y\) para \(y=0\) (22)
No meio 1, o campo é a sobreposição dos campos das ondas incidente e refletida. Contudo, é mostrado no Apêndice 1 que, naquele plano, o fluxo \(I\) é a soma algébrica dos fluxos incidente e refletido, i.e.,
\(I=I_i-I_r\) (23)
com:
\(I_i=-\frac{1}{2}\textrm{Re}\left [ \vec{E}_{i}^{*}\wedge \vec{H}_i \right ]_y=-\frac{1}{2\omega\mu_0}\left [ \vec{E}_{i}^{*}\wedge \left ( \vec{k}^{\left ( i \right )}\wedge \vec{E}_i \right ) \right ]_y=\frac{k^{\left ( i \right )}}{2\omega\mu_0}\left | \vec{E}_i \right |^2\cos\theta_i\) (24)
\(I_r=\frac{1}{2}\textrm{Re}\left [ \vec{E}_{r}^{*}\wedge \vec{H}_r \right ]_y=-\frac{1}{2\omega\mu_0}\textrm{Re}\left [ \vec{E}_{r}^{*}\wedge \left ( \vec{k}^{\left ( r \right )}\wedge \vec{E}_r \right ) \right ]_y=\frac{k^{\left ( i \right )}}{2\omega\mu_0}\left | \vec{E}_r \right |^2\cos\theta_i\) (25)
onde se usou \(\left | \vec{k}^{\left ( i \right )} \right |=\left | \vec{k}^{\left ( r \right )} \right |\) \(\theta_i=\theta_r\). Define-se o coeficiente de reflexão, ou refletância, por:
\(R_\parallel =\frac{I_r}{I_i}=\left | r_\parallel \right |^2\) (26)
com \(r_\parallel\) na equação (13), notando-se que este coeficiente se anula no ângulo de Brewster.
Analogamente, para o meio 2, tem-se:
\(I_t=-\frac{1}{2}\textrm{Re}\left [ \vec{E}_{t}^{*}\wedge \vec{H}_t \right ]_y=-\frac{1}{2\omega\mu_0}\textrm{Re}\left [ \vec{E}_{t}^{*}\wedge \left ( \vec{k}^{\left ( t \right )}\wedge \vec{E}_t \right ) \right ]_y=\frac{1}{2\omega\mu_0}\left | \vec{E}_t \right |^2\textrm{Re}\left [ k^{\left ( t \right )}\cos\theta_t \right ]\) (27)
Define-se o coeficiente de transmissão, ou transmitância, por:
\(T_\parallel =\frac{I_t}{I_i}=\left | t_\parallel \right |^2\textrm{Re}\left [ \frac{k^{\left ( t \right )}\cos\theta_t}{k^{\left ( i \right )}\cos\theta_i} \right ]\) (28)
No Apêndice 2 é demonstrada a conservação genérica da energia na interface, i.e., a energia incidente reparte-se pelas ondas refletida e transmitida:
\(R_\parallel +T_\parallel =1\) (29)
A) No caso de o segundo meio também ser um dielétrico com \(\eta_2>\eta_1\), obtém-se:
\(T_\parallel =\left | t_\parallel \right |^2\textrm{Re}\left [ \frac{\eta_2\cos\theta_t}{\eta_1\cos\theta_i} \right ]\) (30)
Para \(\eta_1>\eta_2\), esta expressão mantém-se válida até ao ângulo limite, onde se anula, permanecendo nula para maiores ângulos de incidência para os quais é cos \(\theta\) imaginário puro.
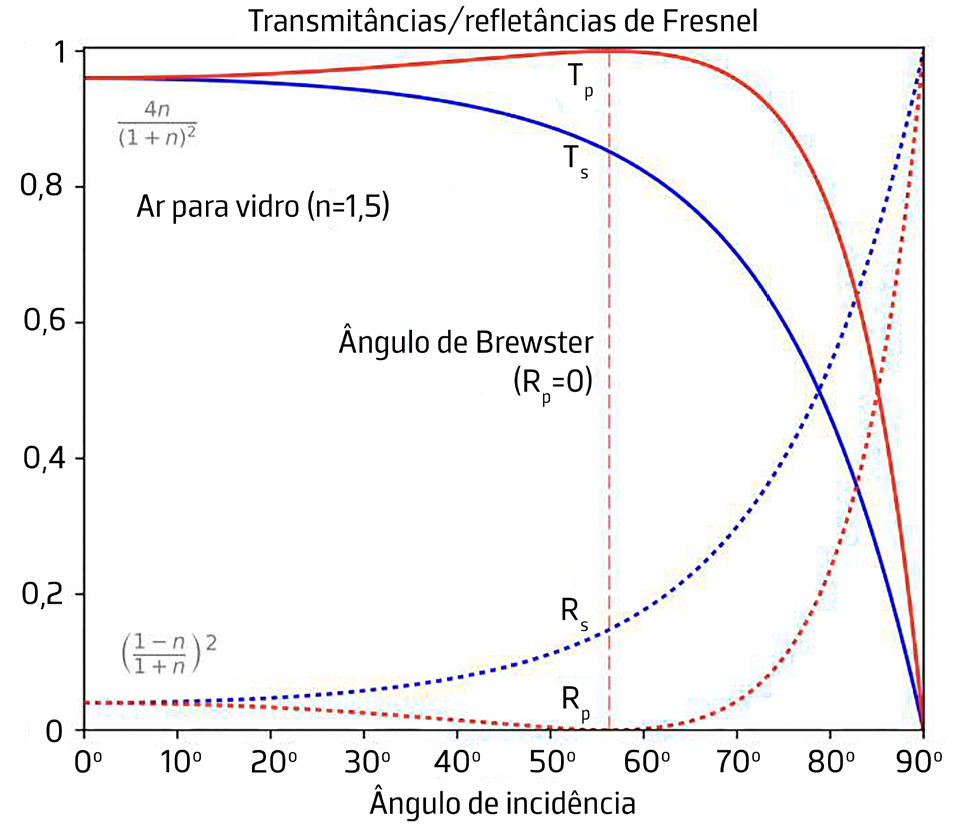
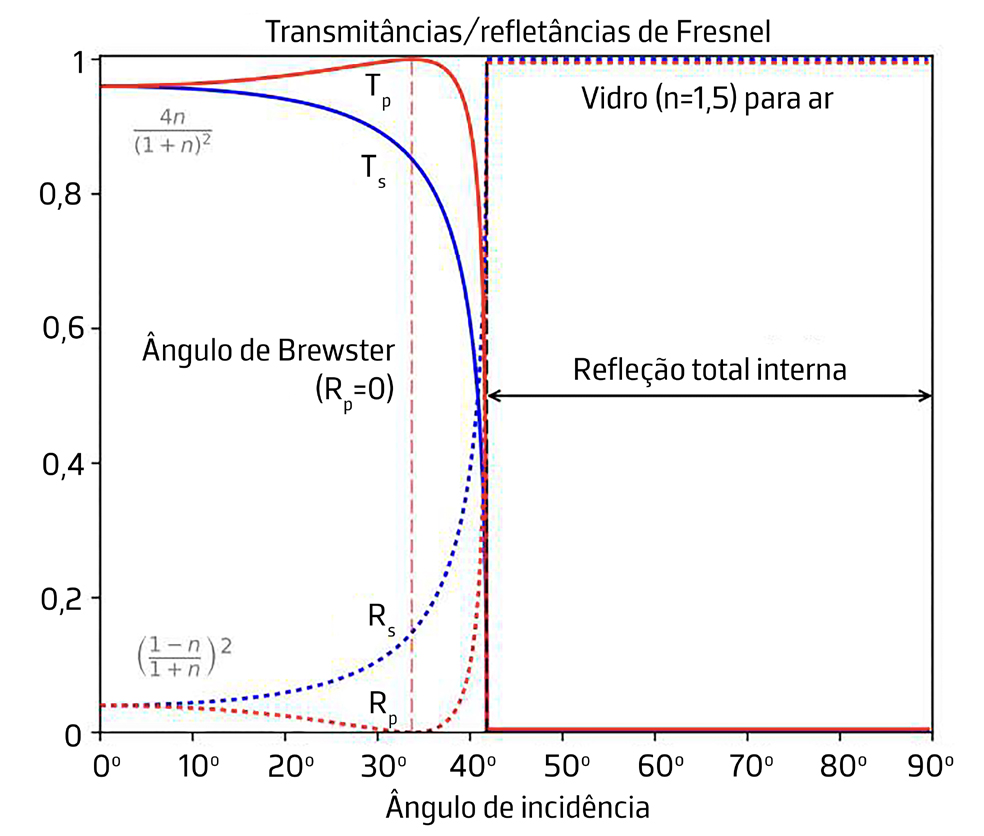
Na FIGURA 5 estão representadas (a vermelho) a refletância e transmitância no caso da interface ar/vidro; na FIGURA 7, estas mesmas grandezas são representadas para a interface vidro/ar.
B) No caso de o segundo meio ser um bom condutor, usando as equações (27) e (19), tem-se:
\(T_\parallel \simeq \frac{4}{\eta_1\cos\theta_i}\sqrt{\frac{2\omega\varepsilon _0}{\sigma}}\ll 1\) (31)
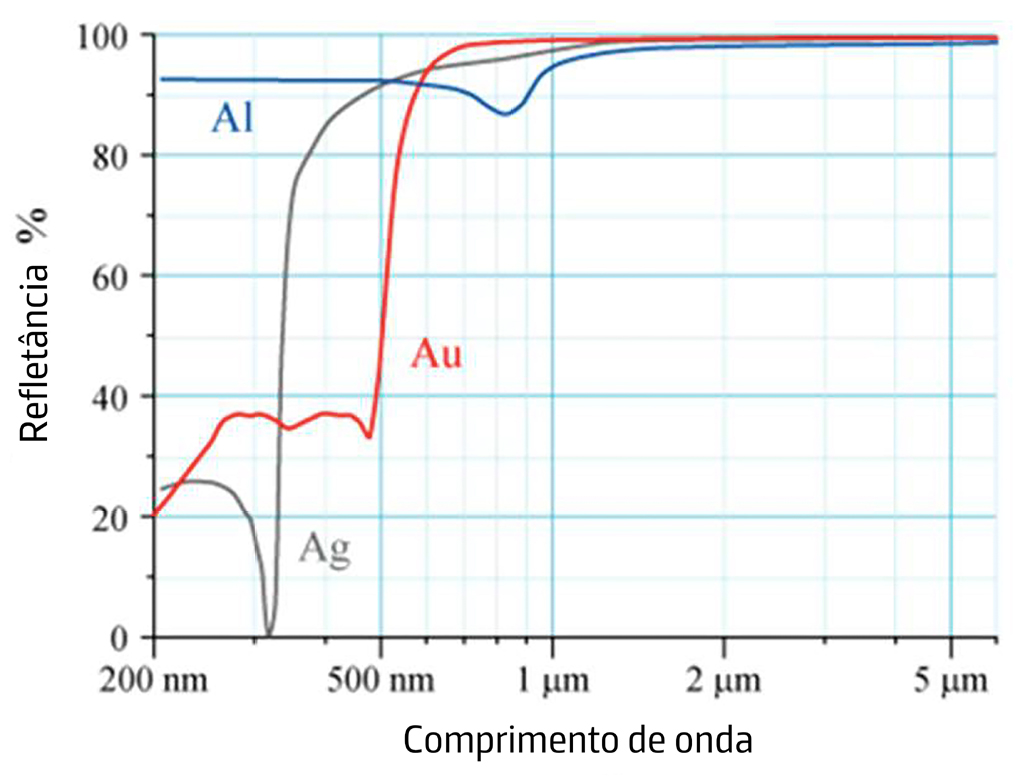
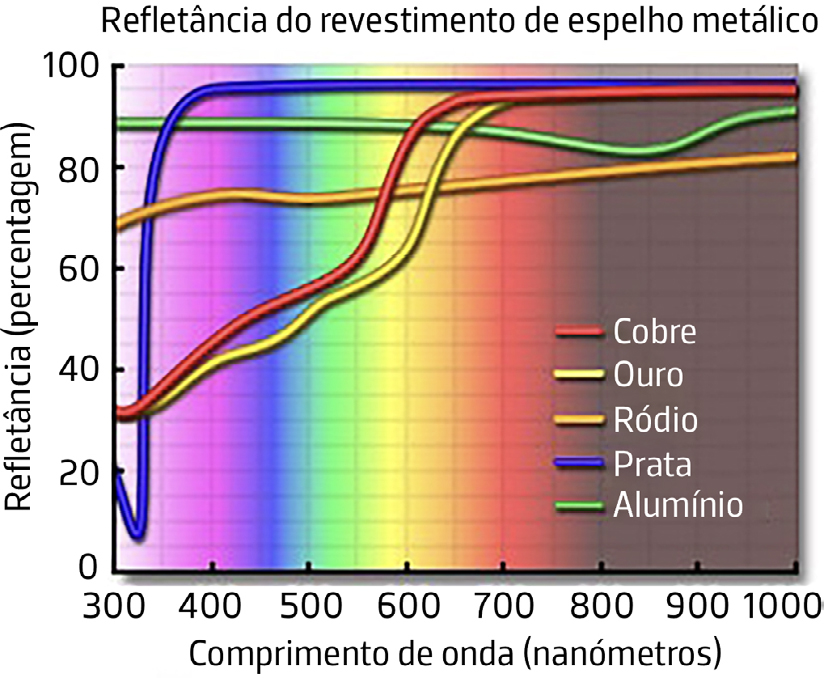
Para a prata \(\left ( \sigma=6,2\times 10^7\Omega^{-1}m^{-1} \right )\) obtém-se \(R_\parallel \sim \) 95% para luz visível. A FIGURA 2 mostra a refletância de alguns metais (meio 1 é vazio ou ar) em função do comprimento de onda, para incidência normal. O súbito decréscimo da refletância na prata para \(\lambda\simeq \) 300nm deve-se à existência de um gap no espectro eletrónico.
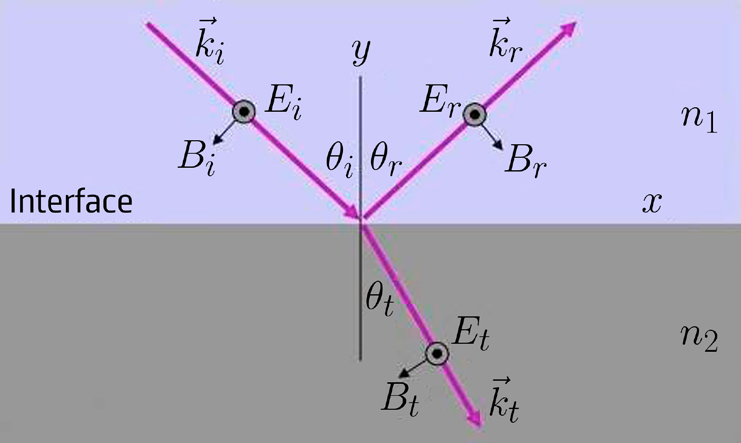
Componentes perpendiculares.
A FIGURA 3 representa o plano de incidência, indicando-se, para as três ondas, as componentes perpendiculares do campo elétrico (pequenos círculos negros) e os respectivos campos magnéticos. Da continuidade das componentes tangenciais do campo elétrico, tira-se:
\(E_i+E_r=E_t\) (32)
Quanto ao campo magnético, a continuidade das suas componentes tangenciais e a equação (7) dão:
\(k^{\left ( i \right )}\left ( E_i-E_r \right )\cos\theta_i=k^{\left ( t \right )}E_t\cos\theta_t\) (33)
A continuidade das componentes normais do campo magnético dá uma identidade quando se usa a lei de Snell.
Das duas equações acima, resulta:
\(r_\perp \equiv \frac{E_r}{E_i}=\frac{k^{\left ( i \right )}\cos\theta_i-k^{\left ( t \right )}\cos\theta_t}{k^{\left ( i \right )}\cos\theta_i+k^{\left ( t \right )}\cos\theta_t}\)
\(t_\perp \equiv \frac{E_r}{E_i}=\frac{2k^{\left ( i \right )}\cos\theta_i}{k^{\left ( i \right )}\cos\theta_i+k^{\left ( t \right )}\cos\theta_t}\) (34)
A partir daqui a discussão segue o que se fez para as componentes paralelas, prescindindo-se, assim, de repetições ou pormenores irrelevantes.
A) Se o meio 2 é, também, um dielétrico, as equações (34) reescrevem-se:
\(r_\perp =\frac{\eta_1\cos\theta_i-\eta_2\cos\theta_t}{\eta_1\cos\theta_i+\eta_2\cos\theta_t}=\frac{tg\theta_t-tg\theta_i}{tg\theta_t+tg\theta_i}\)
\(t_\perp =\frac{2\eta_1\cos\theta_i}{\eta_1\cos\theta_i+\eta_2\cos\theta_t}=\frac{2tg\theta_t}{tg\theta_t+tg\theta_i}\) (35)
tendo-se usado a lei de Snell para obter as últimas expressões. Para incidência normal, tem-se:
\(r_\perp =\frac{\eta_1-\eta_2}{\eta_1+\eta_2}\)
\(t_\perp =\frac{2\eta_1}{\eta_1+\eta_2}\) (36)
Comparando com a equação (14), a diferença de sinal nas expressões de \(r_\perp\) deve-se unicamente às convenções usadas nas FIGURAS 1 e 3 para medir positivamente os campos elétricos.
De notar que \(r_\perp\) nunca se anula. Assim, se a radiação incidente tiver, por exemplo, polarização elíptica, a radiação refletida sairá polarizada rectilineamente (perpendicular ao plano de incidência) para um ângulo de incidência igual ao ângulo de Brewster.
- Se \(\eta_2>\eta_1\), é sempre \(\theta_t<\theta_i\), pelo que \(-1<\)\( r_\perp <\)\(0\)).
- Se\(\eta_1>\eta_2\), existe o ângulo limite para o qual é \(r_\perp=1\). Acima deste ângulo, \(r_\perp\) e \(t_\perp\) são complexos, com \(\left | r_\perp \right |=1\).
A refletância:
\(R_\perp=\left | r_\perp \right |^2=\left | \frac{tg\theta_t-tg\theta_i}{tg\theta_t+tg\theta_i} \right |^2\) (37)
cresce com o ângulo de incidência para os dois casos anteriores, atingindo o valor \(\cos^2\left ( 2\theta_B \right )\) no ângulo de Brewster e o valor unitário acima do ângulo limite no caso \(\eta_1>\eta_2\).
A transmitância:
\(T_\perp=\left | t_\perp \right |^2\textrm{Re}\left [ \frac{k^{\left ( t \right )}\cos\theta_t}{k^{\left ( i \right )}\cos\theta_i} \right ]\) (38)
obedece, também, à equação (29), anulando-se a partir do ângulo limite no caso \(\eta_1>\eta_2\).
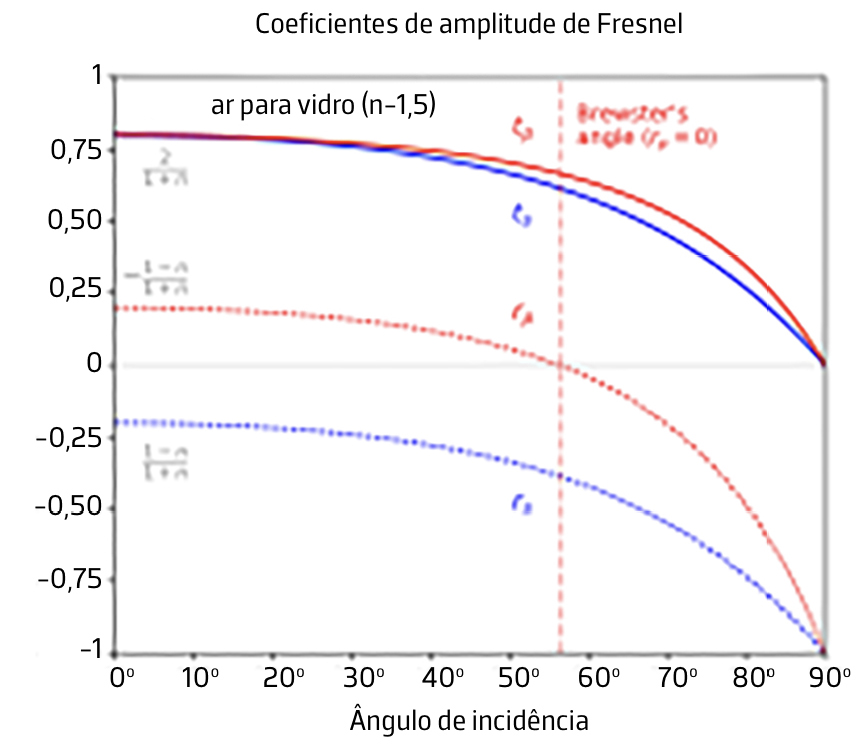
A FIGURA 4 representa as amplitudes relativas para a interface ar/vidro: reflexão (tracejado) e transmissão (cheio), vermelho para as componentes paralelas (p) e azul para as componentes perpendiculares (s).
Na FIGURA 5 são representadas a refletância e transmitância para a mesma interface, com a mesma identificação das curvas.
A FIGURA 6 exibe as amplitudes para a interface vidro/ar, com a mesma convenção interpretativa.
Na FIGURA 7 representam-se as refletância e transmitância para a mesma interface.
B) No caso do meio 2 ser um bom condutor, \(\theta_t\) obtém-se da equação (18), sendo \(\left | \theta_t \right |\ll 1\), pelo que as equações (34) ficam:
\(r_\perp=\frac{\eta_1\cos\theta_i-\left ( 1+i \right )\sqrt{\frac{\sigma}{2\omega\varepsilon _0}}}{\eta_1\cos\theta_i-\left ( 1-i \right )\sqrt{\frac{\sigma}{2\omega\varepsilon _0}}}\sim -1\; \; \; \; \; t_\perp=\frac{2\eta_1\cos\theta_i}{\eta_1\cos\theta_i+\left ( 1+i \right )\sqrt{\frac{\sigma}{2\omega\varepsilon _0}}}\sim 0\) (39)
Observe-se que, neste caso, o campo elétrico tem praticamente um nodo na interface com o condutor. A pequena transmitância é da mesma ordem da que se encontrou para a componente paralela, equação (31) e é nula para o perfeito condutor \(\left ( \sigma=\infty \right )\). A FIGURA 8 exibe a refletância para algumas coberturas metálicas em espelhos.
Tem interesse calcular o momento do campo transferido para o plano separador. Considere- se o meio 1 como ar ou vazio, para simplificar, e o meio 2 condutor. Para incidência normal, o momento transferido em cada segundo, i.e., a pressão exercida é a componente \(\tau _{22}\) do tensor de Maxwell, obtendo-se:
\(\left \langle \tau _{22} \right \rangle=\left \langle u \right \rangle=\frac{1}{4}\varepsilon _0\vec{E}^2+\frac{1}{4}\mu_0\vec{H}^2=\frac{1}{4}\varepsilon _0E_{i}^{2}\left | 1+r_\perp \right |^2+\frac{1}{4}\varepsilon _0E_{i}^{2}\left | 1-r_\perp \right |^2=\frac{1}{2}\varepsilon _0E_{i}^{2}\left ( 1+\left | r_\perp \right |^2 \right )\)
Para bons condutores, tem-se, numa excelente aproximação:
\(\left \langle \tau _{22} \right \rangle\approx \varepsilon _0E_{i}^{2}\) (40)
Este valor é o dobro da pressão para a onda incidente– a pressão é exercida quer por esta onda que atinge a superfície quer pela onda refletida que empurra a superfície.
Para um ângulo de incidência, \(\theta_i\), genérico a pressão exercida obtém-se da equação (40) multiplicada por \(\cos^2\theta_i\).
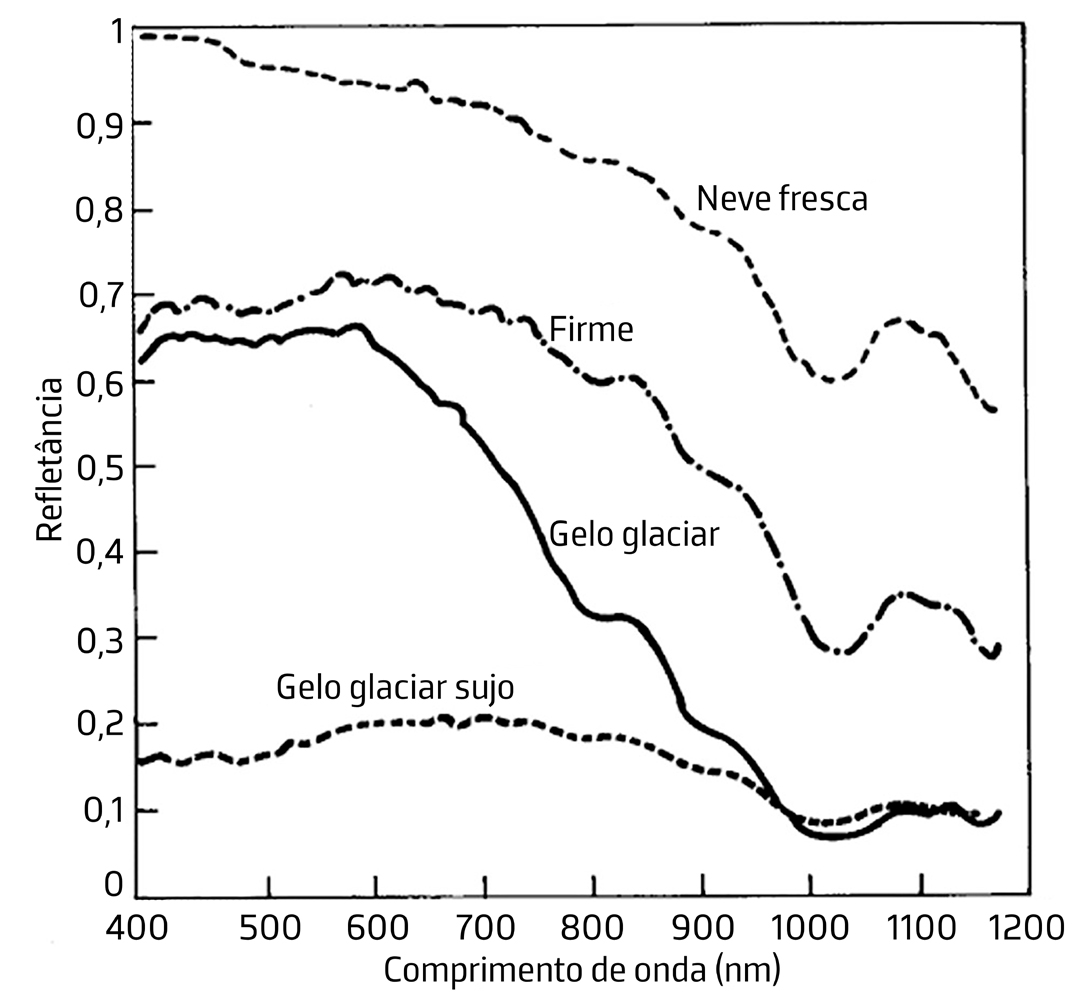
A refletância da água, na sua fase sólida, é de enorme importância em Geofísica e para o aquecimento global (FIGURA 8).
Designa-se por albedo a percentagem de radiação que uma superfície ou um planeta reflete para o espaço. A figura mostra claramente a diminuição de albedo da Terra com o progressivo desaparecimento de glaciares e gelos polares, um fenómeno que se reforça a si próprio pois quanto menos radiação é refletida tanto mais é retida, originando aumento da temperatura média do planeta.
Apêndice 1.
O fluxo de energia como soma de fluxos na interface.
No meio 1, o campo é a sobreposição dos campos das ondas incidente e refletida, de modo que o vetor de Poynting fica:
\(\left \langle \vec{S} \right \rangle=\frac{1}{2}\textrm{Re}\left [ \vec{E}^*\wedge \vec{H} \right ]=\frac{1}{2}\textrm{Re}\left [ \left ( \vec{E}_{i}^{*}+\vec{E}_{r}^{*} \right )\wedge\left ( \vec{H}_i+\vec{H}_r \right ) \right ]=\left \langle \vec{S}_i \right \rangle+\left \langle \vec{S}_r \right \rangle+\frac{1}{2}\textrm{Re}\left [ \vec{E}_{r}^{*}\wedge\vec{H}_i+\vec{E}_{i}^{*}\wedge\vec{H}_r \right ]\)
Os dois últimos termos representam a interferência das duas ondas. Considerando apenas estes termos e para as componentes paralelas, eliminem-se os campos elétricos usando a equação 8, com \(\sigma=0\), para cada onda. Obtém-se:
\(\textrm{Re}\left [ \vec{E}_{r}^{*}\wedge\vec{H}_i+\vec{E}_{i}^{*}\wedge\vec{H}_r \right ]=-\frac{1}{\omega\varepsilon _o\eta_{1}^{2}}\textrm{Re}\left [ \left ( \vec{k}_r\wedge\vec{H}_{r}^{*} \right )\wedge\vec{H}_i+\left ( \vec{k}_i\wedge\vec{H}_{i}^{*} \right )\wedge\vec{H}_r \right ]=\frac{1}{\omega\varepsilon _0\eta_{1}^{2}}\textrm{Re}\left [ \vec{H}_{r}^{*}\cdot\vec{H}_i \right ]\left ( \vec{k}_r+\vec{k}_i \right )\)
onde se usou o facto de os campos magnéticos serem perpendiculares ao plano de incidência. Ora, pretende-se o fluxo de energia no plano de separação, i.e., \(-\left \langle \vec{S}_y \right \rangle\). A expressão anterior vai contribuir com um termo proporcional a \(\left ( \vec{k}_r+\vec{k}_i \right )_y=0\) porque estes vetores de onda têm componentes de sinais opostos em relação à normal ao plano de separação. Deste modo, o fluxo de energia neste plano reduz-se à soma algébrica dos fluxos das ondas incidente e refletida. Para as componentes perpendiculares, eliminam-se os campos magnéticos no termo de interferência, obtendo-se o mesmo resultado.
Apêndice 2.
Conservação de energia na interface.
A) Para as componentes paralelas, reescreva-se a equação (22) para cada uma das ondas, soba forma:
\(I_i=-\frac{1}{2}\textrm{Re}\left [ \vec{E}_{i}^{*}\wedge\vec{H}_i\cdot\vec{e}_y \right ]=-\frac{1}{2}\textrm{Re}\left [ \vec{H}_i\wedge\vec{e}_y\cdot\vec{E}_{i}^{*} \right ]\)
\(I_r=\frac{1}{2}\textrm{Re}\left [ \vec{E}_{r}^{*}\wedge\vec{H}_r\cdot\vec{e}_y \right ]=-\frac{1}{2}\textrm{Re}\left [ \vec{H}_r\wedge\vec{e}_y\cdot\vec{E}_{r}^{*} \right ]\)
\(I_t=-\frac{1}{2}\textrm{Re}\left [ \vec{E}_{t}^{*}\wedge\vec{H}_t\cdot\vec{e}_y \right ]=-\frac{1}{2}\textrm{Re}\left [ \vec{H}_t\wedge\vec{e}_y\cdot\vec{E}_{t}^{*} \right ]\)
onde \(\vec{e}_y\) é o versor da normal ao plano de separação. A continuidade do campo magnético, \(\vec{H}_i+\vec{H}_r=\vec{H}_t\) permite eliminar o campo \(\vec{H}_t\) para se obter:
\(I_i-I_r-I_t=-\frac{1}{2}\textrm{Re}\left [ \vec{H}_i\wedge\vec{e}_y\cdot\left ( \vec{E}_{i}^{*}-\vec{E}_{r}^{*}-\vec{E}_{t}^{*} \right ) \right ]\)
Ora, o campo magnético é, para estas componentes, perpendicular ao plano de incidência (i.e., alinha segundo \(z\)), pelo que \(\vec{H}\wedge\vec{e}_y=-H\vec{e}_x\) para cada uma das ondas acima. Assim:
\(I_i-I_r-I_t=\frac{1}{2}\textrm{Re}\left [ H_i\left ( \vec{E}_{i}^{*}-\vec{E}_{t}^{*} \right )_x+H_r\left ( \vec{E}_{r}^{*}-\vec{E}_{t}^{*} \right )_x \right ]\)
Ora as componentes tangenciais (i.e., segundo \(x\)) do campo elétrico são contínuas, pelo que (FIGURA 1):
\(I_i-I_r-I_t=\frac{1}{2}\textrm{Re}\left [ H_i\left ( \vec{E}_{r}^{*} \right )_x+H_r\left ( \vec{E}_{i}^{*} \right )_x \right ]=\frac{1}{2}\textrm{Re}\left [ H_iE_{r}^{*}-H_rE_{r}^{*} \right ]\cos\theta_i\)
Mas para a onda incidente tem-se \(H_i=\frac{k^{\left ( i \right )}E_i}{\omega\mu_0}\) e, do mesmo modo, para a onda refletida.
Assim:
\(I_i-I_r-I_t=\frac{k^{\left ( i \right )}}{2\omega\mu_0}\textrm{Re}\left [ E_iE_{r}^{*}-E_rE_{i}^{*} \right ]\cos\theta_i=0\)
B) Para as componentes perpendiculares, o raciocínio é semelhante ao anterior. Tem-se:
\(I_i-I_r-I_t=-\frac{1}{2}\textrm{Re}\left [ \vec{E}_{i}^{*}\wedge\vec{H}_i+\vec{E}_{r}^{*}\wedge\vec{H}_r-\vec{E}_{t}^{*}\wedge\vec{H}_t \right ]\cdot\vec{e}_y\)
O campo magnético, contínuo através do plano de separação, permite escrever:
\(I_i-I_r-I_t=-\frac{1}{2}\textrm{Re}\left [ \left ( \vec{E}_{i}^{*}-\vec{E}_{t}^{*} \right )\wedge\vec{H}_i\cdot\vec{e}_y+\left ( \vec{E}_{r}^{*}-\vec{E}_{t}^{*} \right )\wedge\vec{H}_r\cdot\vec{e}_y \right ]=-\frac{1}{2}\textrm{Re}\left [ \vec{e}_y\wedge\left ( \vec{E}_{i}^{*}-\vec{E}_{t}^{*} \right )\cdot\vec{H}_i+\vec{e}_y\wedge\left ( \vec{E}_{r}^{*}-\vec{E}_{t}^{*} \right )\cdot\vec{H}_r \right ]\)
Para estas componentes, os campos elétricos têm a direcção \(z\), de modo que:
\(I_i-I_r-I_t=-\frac{1}{2}\textrm{Re}\left [ \left ( E_{i}^{*}-E_{t}^{*} \right )\left ( \vec{H}_i \right )_x+\left ( E_{r}^{*}-E_{t}^{*} \right )\left ( \vec{H}_r \right )_x \right ]=-\frac{1}{2}\textrm{Re}\left [ E_{r}^{*}H_i-E_{i}^{*}H_r \right ]\cos\theta_i\)
O penúltimo termo resulta da continuidade das componentes tangenciais do campo elétrico; para o último termo, ver FIGURA 3. Ora, para as ondas incidente e refletida, é \(H=\frac{k^{\left ( i \right )}}{\omega\mu_0}E\), obtendo-se, finalmente:
\(I_i-I_r-I_t=-\frac{k^{\left ( i \right )}}{2\omega\mu_0}\textrm{Re}\left [ E_{r}^{*}E_i-E_rE_{i}^{*} \right ]\cos\theta_i=0\)
[editar] Referências
- ↑ AGE, E., Ondas eletromagnéticas, Rev. Ciência Elem., V11(2):027. (2023). DOI: 10.24927/rce2023.027.
- ↑ AGE, E., Ondas, Rev. Ciência Elem., V8(1):016. (2020). DOI: 10.24927/rce2020.016.
- ↑ LAGE, E., Ondas eletromagnéticas, Rev. Ciência Elem., V11(2):027. (2023). DOI: 10.24927/rce2023.027.
Criada em 26 de Abril de 2022
Revista em 14 de Junho de 2022
Aceite pelo editor em 13 de Outubro de 2023

