A Geometria da Regressão Linear
Referência : Gomes, C., (2020) A Geometria da Regressão Linear, Rev. Ciência Elem., V8(4):054
Autor: Carlos Gomes
Editor: José Ferreira Gomes
DOI: [https://doi.org/10.24927/rce2020.054]

[editar] Resumo
A regressão linear é um tema normalmente explorado (nas escolas) com recurso a uma calculadora científica gráfica ou software da moda (GeoGebra ou Desmos, por exemplo), ficando os estudantes com a tarefa aborrecida de introduzir números em listas e obter como recompensa uma equação que utilizam para fazer previsões num dado contexto. O que aqui se trata é de mostrar o grande valor didático deste problema, mobilizando conhecimentos que os alunos detêm para aclarar, do ponto de vista geométrico, o que está em causa em todo este processo que decorre nos “bastidores” da tecnologia.
A geometria do problema
O problema que consiste na determinação da reta que melhor se ajusta a uma dada nuvem de \(n\) pontos \(\left ( x_{i},y_{i} \right )\) é tradicionalmente tratado como o problema de encontrar os parâmetros \(a\) e \(b\) da equação \(y=ax+b\) que minimizam a soma \(S=\sum_{i=1}^{n}d_{i}^{2}\), em que os \(d_{i}\) são as diferenças entre os valores observados e os valores do modelo, isto é, \(d_{i}=y_{i}-ax-b\).
Sejam \(\left ( x_{1},y_{1} \right )\), \(\left ( x_{2},y_{2} \right )\),..., \(\left ( x_{n},y_{n} \right )\) os dados observados (nuvem de pontos na FIGURA 1). Para a determinação do parâmetro \(a\) (declive da reta), seria “simpático” que a nuvem tivesse o seu centro de massa na origem do referencial, isto é, no ponto de coordenadas (0; 0). Isto porque libertar-nos-íamos do parâmetro \(b\) da equação da reta, o que parece reduzir a dificuldade do problema, pois, nesta condições, o modelo associado à reta de regressão seria \(y = ax\). Para fazer com que o centro de massa da nuvem se desloque para a origem, é suficiente efetuarmos uma translação de toda a nuvem de pontos segundo o vetor \(\left ( -\bar{x},-\bar{y} \right )\), ou seja, basta subtrairmos o centro de massa \(\left ( \bar{x},\bar{y} \right )\) a todos os pontos da nuvem. Obtém-se assim uma nova nuvem de pontos da forma \(\left ( x_{i}-\bar{x},y_{i}-\bar{y} \right )\) cujo centro de massa é (0; 0).
Fazendo \(x_{i}-\bar{x}=\tilde{x}_{i}\) e \(y_{i}-\bar{y}=\tilde{y}_{i}\), a nuvem sobre a qual o trabalho prossegue será \(\left ( \tilde{x}_{i},\tilde{y}_{i} \right )\), com \(i=1,2,...,n\), cuja reta de regressão tem o mesmo declive que a reta de regressão da nuvem original, em consequência da translação efetuada.
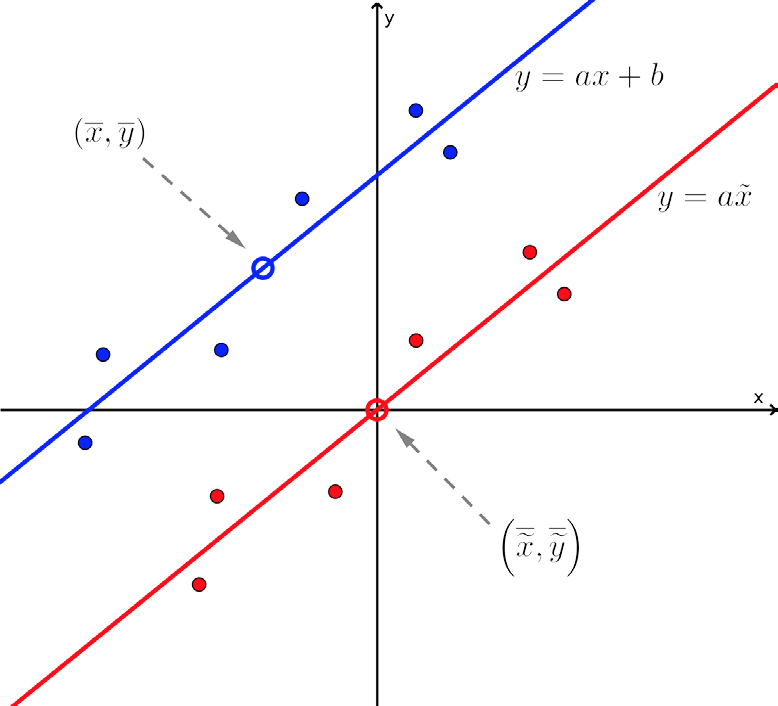
A nova nuvem é constituída por pontos da forma \(\left ( \tilde{x}_{i},\tilde{y}_{i} \right )\) e os pontos da forma \(\left ( \tilde{x}_{i},a\tilde{x}_{i} \right ),i=1,2,...,n\), são os pontos sobre a reta \(\tilde{y}=a\tilde{x}\), que coincidiriam com os primeiros caso a correlação fosse perfeita. Os \(n\) vetores \(\vec{u}_{i}=\left ( \tilde{x}_{i},a\tilde{x}_{i} \right )\) determinados por estes pontos são colineares. Mas aqui, uma mudança de dimensão vai tornar o trabalho mais simples: em vez de considerarmos estes \(n\) vetores de dimensão 2, utilizamos os dados organizados em vetores de dimensão n:
\(\vec{i}=\left ( \tilde{x}_{1},\tilde{x}_{2},...,\tilde{x}_{n} \right ),\)
\(\vec{j}=\left ( a\tilde{x}_{1},a\tilde{x}_{2},...,a\tilde{x}_{n} \right ),\)
e
\(\vec{u}=\left ( \tilde{y}_{1},\tilde{y}_{2},...,\tilde{y}_{n} \right )\).
Os vetores \(\vec{i}\) e \(\vec{j}\) são colineares:
\(\vec{j}=\left ( a\tilde{x}_{1},a\tilde{x}_{2},...,a\tilde{x}_{n} \right )\)
\(=a\left ( \tilde{x}_{1}\tilde{x}_{2},...,\tilde{x}_{n} \right )\) (1)
\(=a\vec{i}\).
Para além do mais, o escalar \(a\) em (1) é precisamente o declive da reta procurada! Assim, determinar \(a\) será equivalente a determinar (algo sobre) \(=\vec{j}\), agora num espaço de dimensão \(n\), (veja-se o apêndice da versão eletrónica para clarificação deste ponto).
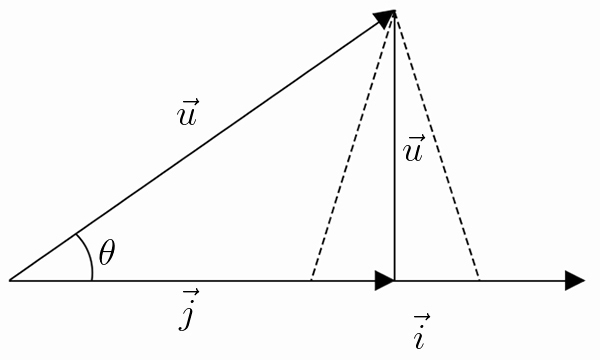
Repare-se que \(\vec{u}-\vec{j}=\left ( \tilde{y}_{1}-a\tilde{x}_{1},...,\tilde{y}_{n}-a\tilde{x}_{n} \right )\) não é mais do que o vetor dos resíduos, isto é, o vetor cujas componentes são as diferenças entre os dados observados e os dados teóricos da nova nuvem. Ora, o que se pretende é que a norma (ou distância) \(\left \| \vec{u}-\vec{j} \right \|\) seja mínima. Isto só acontecerá se \(\vec{u}-\vec{j}\) for normal a \(\vec{u}\) (como sugere a FIGURA 2). Para que tal aconteça, \(\vec{j}\) tem de ser a projeção de \(\vec{u}\) sobre \(\vec{i}\). Logo, o produto escalar de \(\vec{u}-\vec{j}\) com \(\vec{i}\) tem de ser nulo, retirando-se desta condição o valor do multiplicador \(a\), declive da reta de regressão:
\(\begin{matrix} \left ( \vec{u}-\vec{j} \right )\cdot \vec{i}=0\\ \Leftrightarrow \left ( \vec{u}-a\vec{i} \right )\cdot \vec{i}=0\; \; \; \left ( \vec{j}=a\vec{i}, de \left ( 1 \right ) \right )\\ \Leftrightarrow \vec{u}\cdot \vec{i}-a\vec{i}=0\\ \Leftrightarrow a=\frac{\vec{u}\cdot \vec{i}}{\left \| \vec{i} \right \|}\; \; \; \left ( \vec{i}\cdot \vec{i}=\left \| \vec{i} \right \|^{2} \right ) \end{matrix}\). (2)
Depois de se calcular \(a\) através de (2), a determinação do parâmetro \(b\) é um simples exercício: dado que \(\left ( \bar{x},\bar{y} \right )\) pertence à reta procurada, ele terá de satisfazer a condição \(y = ax + b\). Daqui se retira que \(b=\bar{y}-a\bar{x}\).
Exemplos de aplicação
Exemplo 1
Vejamos a aplicação destes resultados a um exercício típico de um manual escolar.
Existirá alguma relação entre a temperatura e a quantidade de chuva que cai em Amarante? Para responder a esta pergunta vamos comparar num gráfico de correlação as temperaturas médias (ºC) dos vários meses do ano com a pluviosidade média (mm).
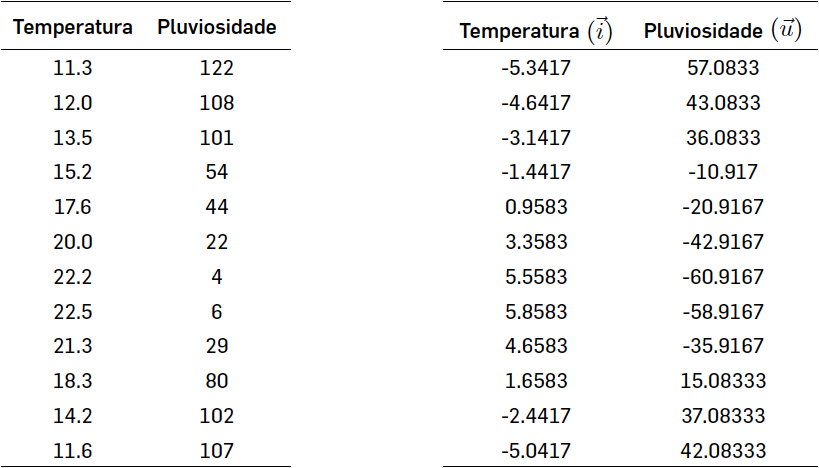
Neste exemplo, a tabela da esquerda é dada e a da direita foi calculada por nós. O centróide da nuvem de pontos é \(\left ( \bar{x},\bar{y} \right )=\left ( 16.6417,64.9167 \right )\). Os vetores \(\vec{u}\) e \(\vec{i}\) são as colunas da tabela da direita, depois de efetuada a translação da nuvem original: são vetores num espaço de dimensão 12.
De acordo com as conclusões da secção anterior, os parâmetros da equação da reta de regressão \(y = ax + b\) podem ser calculados do seguinte modo:
\(\begin{matrix} a=\frac{\vec{u}\cdot \vec{i}}{\left \| \vec{i}^{2} \right \|}\\ \approx \frac{-1895.4583}{195.2692}\\ \approx -9.7069,\\ b=\bar{y}-a\bar{x}\\ \approx 64.9167+9.7069\times16.6417\\ \approx 226.4557. \end{matrix}\)
Assim, \(y \approx −9.7069x + 226.4557\) será a equação da reta de regressão e, com ela, podemos fazer estimativas no contexto do problema.
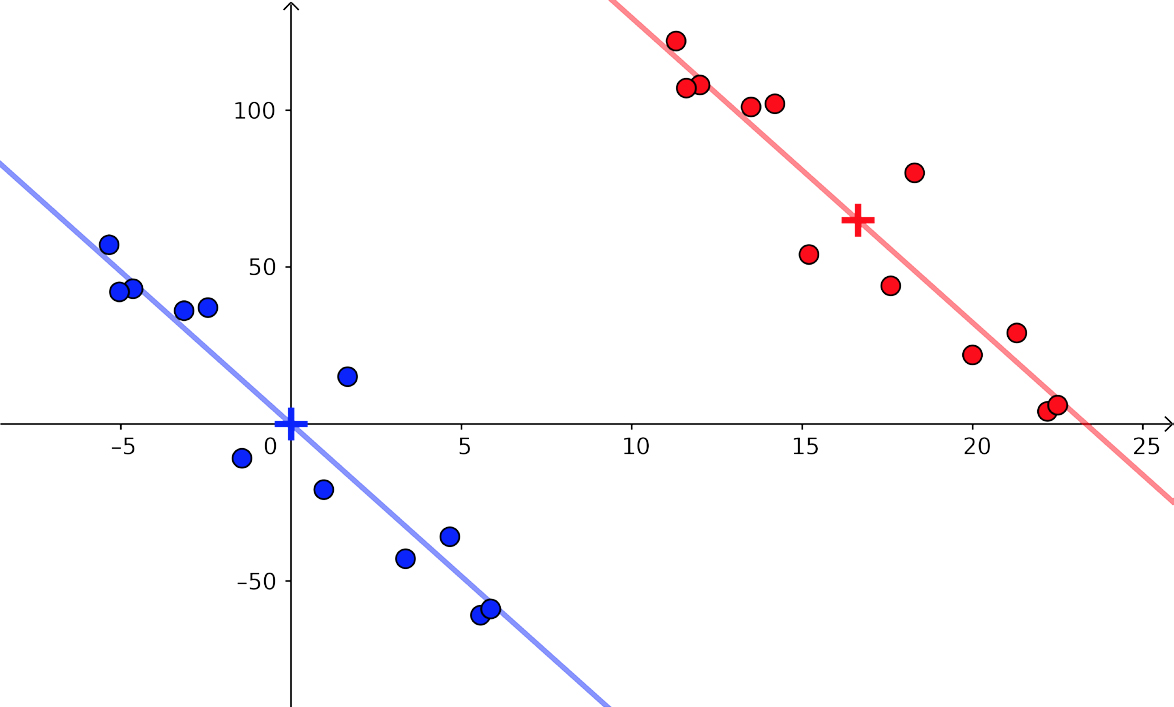
Note-se que o produto escalar de dois vectores de dimensão \(n\) não é mais do que a soma dos produtos das correspondentes componentes desses vectores (uma generalização do que se faz para \(n = 2\) ou \(n = 3\), na disciplina de Matemática A no Ensino Secundário), ou seja, se \(\vec{a}=\left ( a_{1},a_{2},...,a_{n} \right )\) e \(\vec{b}=\left ( b_{1},b_{2},...,b_{n} \right )\),
\(\vec{a}\cdot \vec{b}=a_{1}\times b_{1}+a_{2}\times b_{2}+\cdots +a_{n}\times b_{n}=\sum_{i=1}^{n}a_{i}\times b_{i}\)
Também a norma de um vector de dimensão n é uma generalização da norma de vetores em 2 e 3 dimensões, isto é,
\(\left \| \vec{a} \right \|=\sqrt{a_{1}^{2}+a_{2}^{2}+\cdots +a_{n}^{2}}=\sqrt{\sum_{i=1}^{n}a_{i}^{2}}\)
assim, no presente exemplo, \(\vec{u}\cdot \vec{i}\) corresponde a efectuar a soma dos produtos dos elementos correspondentes de cada linha da tabela da direita.
Exemplo 2
Neste exemplo, aplicaremos os conceitos anteriores à construção de um modelo linear do número de infetados pelo novo coronavírus em função do tempo decorrido no período de 8 a 31 de maio. Aqui, o centro de massa é dado pelas coordenadas do ponto \(\left ( \bar{x},\bar{y} \right )=\left ( 11.5,29648.583 \right )\) e os vetores \(\vec{i}\) e \(\vec{u}\) habitam um espaço de dimensão 24 (colunas da tabela da direita).
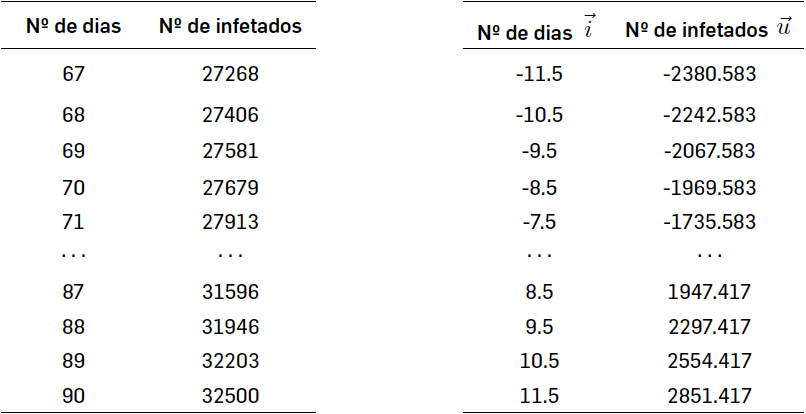
O produto escalar é \(\vec{u}\cdot\vec{i}\simeq 261980\) (soma dos produtos dos elementos de cada linha da tabela de baixo). O quadrado da norma do vetor \(\vec{i}\) (quadrância de \(\vec{i}\)) é \(\left \| \vec{i} \right \|^{2}=1150\).
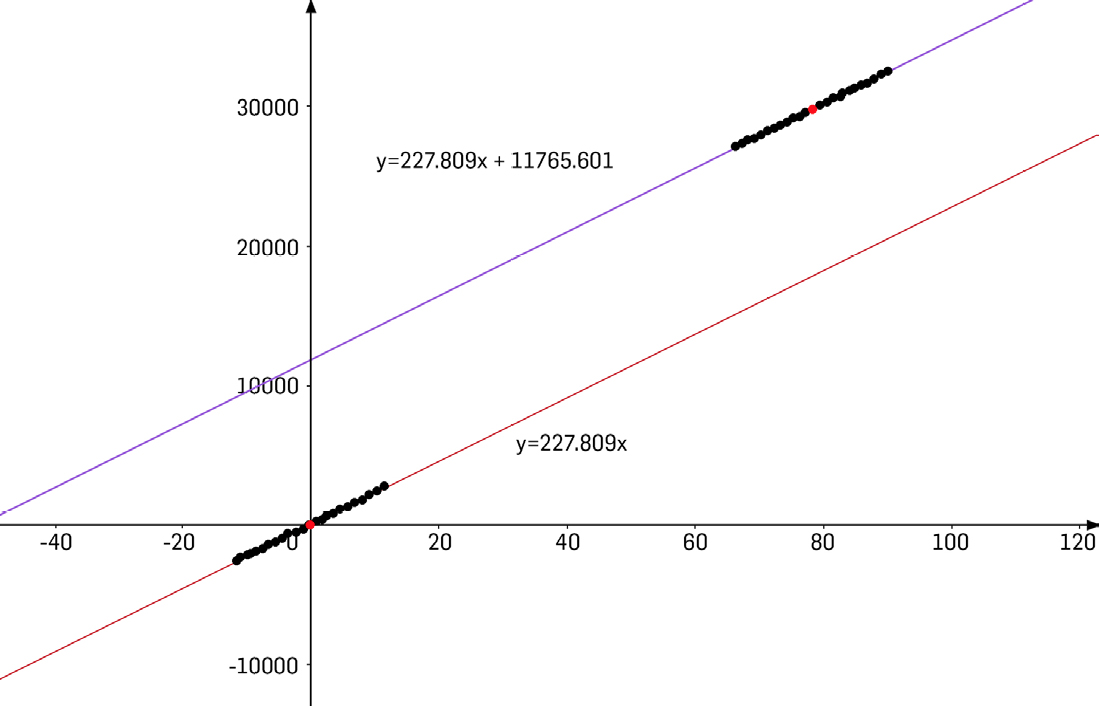
Assim, com \(a=\frac{261980}{1150}\simeq 227.809\) e \(b=\bar{y}-a\bar{x}\simeq 11765.601\), obtemos a equação da reta mostrada na figura acima.
O leitor pode criar uma lição no Geogebra Classroom com este exemplo, seguindo para https://www.geogebra.org/m/ncpffvne
Coeficiente de correlação linear
O coeficiente de correlação é uma medida que pretende determinar o grau de alinhamento dos dados. Sobre ele costumam ser colocadas duas questões:
- Por que razão varia no intervalo \([−1, 1]\)?
- Por que razão a correlação entre as variáveis é tanto mais forte quanto mais próximo de \(−1\) ou de \(1\) se encontra o coeficiente? Não seria razoável pensarmos que quanto mais próximo de zero mais forte será a correlação, uma vez que ele mede o grau de proximidade dos dados em relação à reta?!
Repare-se que o coeficiente de correlação, sendo uma medida do alinhamento dos dados, deve estar relacionado com o “grau de colinearidade” entre os vetores \(\vec{u}\) e \(\vec{i}\), referentes aos dados transladados (note que a correlação não depende da nuvem que se considera, uma vez que a operação de translação efetuada à nuvem inicial garante a manutenção das relações entre os dados observados e os teóricos). E uma forma natural de medir este “grau de colinearidade” é estudando o ângulo \(\theta\) que \vec{u} e \vec{i} formam entre si (ver FIGURA 2). (Note que em tudo o que se segue se pode substituir a unidade grau por rad.). Assim, \(\theta\) poderia ser usado com legitimidade como medida do grau de alinhamento dos dados, ou seja, como coeficiente de correlação. O diagrama da FIGURA 5 resume a variação deste coeficiente de correlação.
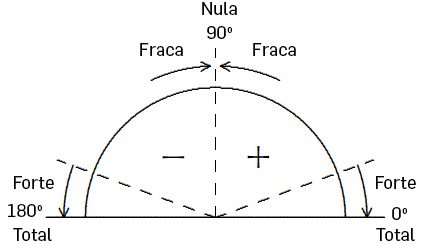
Visto que \(cos\theta =\frac{\vec{u}\cdot\vec{i}}{\left \| \vec{u} \right \|\left \| \vec{i} \right \|}\), \(\theta\) pode ser obtido através de
\(\theta =arcos\left ( \frac{\vec{u}\cdot\vec{i}}{\left \| \vec{u} \right \|\left \| \vec{i} \right \|} \right )\). (3)
No exemplo 1 da secção anterior, o coeficiente de correlação \(\theta\) é
\(\theta =arcos\left ( \frac{\vec{u}\cdot\vec{i}}{\left \| \vec{u} \right \|\left \| \vec{i} \right \|} \right )=arcos\left ( \frac{-1895.4583}{143.7391\times 13.9739} \right )=160.68^{\circ}\) (forte Negativa?).
e no segundo exemplo, \(\theta =arcos\left ( \frac{2,61980}{2,62579.265} \right )=arcos\left ( 0.998 \right )\simeq 3.62^{\circ}\) (Muito forte, positiva?).
No entanto, na literatura sobre o assunto, \(\theta\) é convenientemente substituído pelo seu cosseno (porquê?), e assim se compreende a sua variação tal como encontramos nos manuais:
\(0^{\circ}\leq \theta\leq 180^{\circ}\Rightarrow -1\leq cos\theta\leq 1\Leftrightarrow -1\leq \frac{\vec{u}\cdot\vec{i}}{\left \| \vec{u} \right \|\left \| \vec{i} \right \|}\leq 1\).
Uma fórmula que normalmente acompanha os manuais para determinar o valor do coeficiente de correlação,\(r\), é
\(r=\frac{\sum_{i=1}^{n}x_{i}y_{_{i}}-\frac{\left ( \sum_{i=1}^{n}x_{i} \right )\left ( \sum_{i=1}^{n}y_{i} \right )}{n}}{\sqrt{\left ( \sum_{i=1}^{n}x_{i}^{2}-\frac{\left ( \sum_{i=1}^{n} \right )^{2}}{n} \right )\left ( \sum_{i=1}^{n}y_{i}^{2}-\frac{\left ( \sum_{i=1}^{n}y_{i} \right )^{2}}{n} \right )}}\) (4)
Sendo (4) equivalente a
\(r=\frac{\sum_{i=1}^{n}\left ( x_{i}-\bar{x} \right )\left ( y_{i}-\bar{y} \right )}{\sqrt{\sum_{i=1}^{n}\left ( x_{i}-\bar{x} \right )^{2}}\sqrt{\sum_{i=1}^{n}\left ( y_{i}-\bar{y} \right )^{2}}}\)
fica estabelecida a igualdade
\(r=\frac{\vec{u}\cdot\vec{i}}{\left \| \vec{u} \right \|\left \| \vec{i} \right \|}=cos\theta\)
Apêndice
A interpretação geométrica que se explora neste texto tem como elemento essencial a translação da nuvem de pontos original para uma nuvem de pontos com centro de massa na origem do referencial. Esta operação faz com que os dados transladados cumpram
\(\sum_{i=1}^{n}\tilde{x}_{i}=0\) e \(\sum_{i=1}^{n}\tilde{y}_{i}=0\).
Reescrevendo estas condições, ficamos com
\(\begin{matrix} \sum_{i=1}^{n}\tilde{x}_{i}=0\Leftrightarrow 1\times \tilde{x}_{1}+1\times\tilde{x}_{2}+\cdots +1\times \tilde{x}_{n}=0\\ \Leftrightarrow \vec{w}\cdot\vec{i}=0\\ \sum_{i=1}^{n}\tilde{y}_{i}=0\Leftrightarrow 1\times \tilde{y}_{1}+1\times\tilde{y}_{2}+\cdots +1\times \tilde{y}_{n}=0\\ \Leftrightarrow \vec{w}\cdot\vec{u}=0 \end{matrix}\)
que, do ponto de vista geométrico, permitem afirmar que os vectores \(\vec{i}\) e \(\vec{u}\) (e, consequentemente, \(\vec{j}\)) são perpendiculares ao vector unitário \(w = (1, 1, · · · , 1)\). Assim, \(\vec{i}\), \(\vec{j}\) e \(\vec{u}\) habitam o hiperplano de dimensão \(n − 1\), normal ao vector unitário \vec{w}. Este facto não altera a argumentação seguida pois no hiperplano de dimensão \(n − 1\) continuamos a querer reduzir ao mínimo a norma de \(\vec{u}-\vec{j}\) e a condição continua a ser a ortogonalidade deste vector a \(\vec{j}\).
No caso em que a amostra observada é constituída apenas por dois pontos, \(\vec{i}\), \(\vec{j}\) e \(\vec{u}\) são colineares e a correlação é perfeita, como seria de esperar. Para a situação em que \(n = 3\), pode manipular e descarregar a animação GeoGebra em https://www.geogebra. org/m/muxygsbz
Conclusão
Ao longo dos anos, o tema da regressão linear tem sido tratado nas nossas escolas, quase exclusivamente, como uma manipulação de fórmulas, à qual a tecnologia veio retirar algum desse desprazer salvando, por um lado, os alunos dos cálculos fastidiosos, mas atirando-os, por outro, para uma cegueira determinada pela calculadora gráfica. O que aqui se quis mostrar foi que essas abordagens tradicionais ao tema podem, com enormes vantagens, serem substituídas por uma abordagem geométrica sólida, coerente e palpável, em que a única novidade (mas não surpresa) reside na generalização de conceitos de geometria analítica a espaços de dimensão superior a três. Para além disso, abre também espaço à compreensão dos “bastidores” da calculadora gráfica, permitindo que os alunos olhem para ela como uma biblioteca de algoritmos que podem compreender e até criar.
[editar] Referências
Criada em 25 de Abril de 2020
Revista em 28 de Abril de 2020
Aceite pelo editor em 15 de Dezembro de 2020

