Lei de Ohm
Referência : Ferreira, M., (2015) Lei de Ohm, Rev. Ciência Elem., V3(2):029
Autor: Miguel F.
Editor: Joaquim Agostinho Moreira
DOI: [http://doi.org/10.24927/rce2015.029]

Em 1827, Georg Ohm (1787 – 1854), após investigações sobre a condução eléctrica, concluiu que para um condutor metálico, a uma dada temperatura fixa, a razão entre a diferença de potencial entre os seus terminais e a intensidade de corrente que o atravessa é constante. Este enunciado constitui a Lei de Ohm.
Matematicamente, a Lei de Ohm pode ser escrita da seguinte forma:
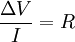
em que a constante R tem o nome de Resistência eléctrica e é característica do condutor e da sua geometria. Assim, a representação gráfica da diferença de potencial em função da intensidade de corrente é uma linha recta, cujo declive corresponde ao valor da resistência.
No caso do condutor ter a forma de um sólido de secção recta de área constante, como por exemplo, um cilindro ou um parelelepipedo regular, a resistência eléctrica é dada pelo produto da resistividade do material (ρ) de que é feito o meio condutor e de um factor geométrico, que, neste caso, é igual à razão entre o comprimento (L) e a área da secção recta (A):
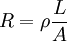
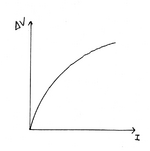
Nem todos os condutores obedecem à lei de Ohm. Para esses condutores o gráfico que relaciona a diferença de potencial com a intensidade de corrente não é linear. Por essa razão são chamados de condutores não-lineares, por oposição aos condutores que obedecem à lei de Ohm – chamados condutores lineares. Nos condutores não lineares, o valor da resistência para um dado valor de intensidade de corrente, corresponde ao declive da recta tangente do gráfico da função 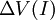 . Como o gráfico não é linear, esse declive varia, logo, também é variável a resistência oferecida por esses condutores à passagem de corrente.
. Como o gráfico não é linear, esse declive varia, logo, também é variável a resistência oferecida por esses condutores à passagem de corrente.
Criada em 07 de Novembro de 2010
Revista em 25 de Fevereiro de 2011
Aceite pelo editor em 26 de Fevereiro de 2011
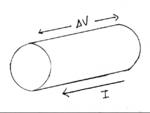
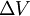 percorrido por uma corrente I.
percorrido por uma corrente I.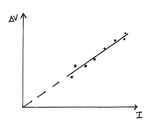
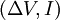 distribuem-se adequadamente em torno de uma linha recta.
distribuem-se adequadamente em torno de uma linha recta.