Lei da gravitação universal

Referência : Araújo, M. (2010), WikiCiências, 1(9):0003
Autor: Mariana de Araújo
Editor: Joaquim Agostinho Moreira

---

---

A força gravitacional entre dois corpos pontuais com massas m₁ e m₂ é directamente proporcional ao produto das massas, inversamente proporcional ao quadrado da distância entre eles. A força tem a direcção da recta que os une.

Matematicamente, a força que o corpo 1 exerce sobre o corpo 2 é dada por

$\vec{F}_{12} = -G\dfrac{m_1 m_2}{\vert \vec{r}_{12} \vert^2}\hat{e}_{12}$

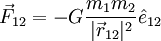
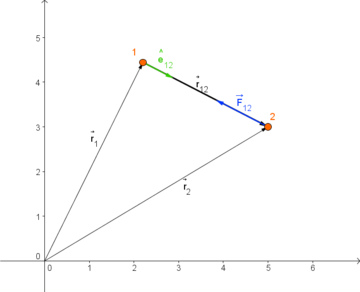
em que 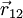$\vec{r}_{12}$ é o vector com origem no corpo 1 e extremidade no corpo 2, e 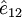$\hat{e}_{12}$ é um vector unitário com a direcção e sentido de 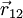$\vec{r}_{12}$, como ilustrado na figura 1.

G é a constante de gravitação universal, que no Sistema Internacional tem o valor 6.67428E-11 m³kg^-1s².

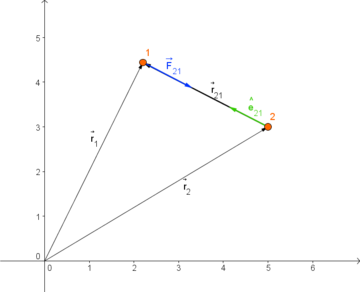
A força que o corpo 2 exerce sobre o corpo 1, 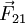$\vec{F}_{21}$ é simétrica à força 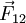$\vec{F}_{12}$ e aplicada no corpo 2:

$\vec{F}_{21} = -G\dfrac{m_2 m_1}{\vert \vec{r}_{21} \vert^2}\hat{e}_{21}$

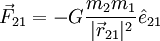
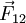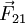como indicado na figura 2. Note-se que $\vec{F}_{12}$ e $\vec{F}_{21}$ formam um par acção-reacção.

A lei da gravitação universal foi enunciada por Isaac Newton (1643-1727) em 1687 na sua obra Philosophiæ Naturalis Principia Mathematica. Esta lei explicita a forma da força atractiva que existe entre dois corpos devido ao facto de terem massa, mas nada diz sobre a sua origem, que só foi explicada mais tarde pela Teoria da Relatividade Geral de Albert Einstein. Nesta obra Newton também mostrou como as Leis de Kepler são consequência desta lei.

Apesar de ser válida para a maioria dos sistemas gravitacionais observados, há fenómenos que só são explicados utilizando Relatividade Geral. É o caso da precessão da órbita de Mercúrio e da deflexão de raios de luz por efeitos gravitacionais. A Relatividade Geral é mais utilizada quando é requerida uma extrema precisão nos resultados, ou quando os sistemas envolvem corpos muito massivos ou muito densos.

Figura 1

Figura 2

---

Criada em 22 de Julho de 2010
Revista em 22 de Julho de 2010
Aceite pelo editor em 9 de Setembro de 2010