Condutividade

Referência : Ferreira, M., (2015) Condutividade, Rev. Ciência Elem., V3(1):012
Autor: Miguel F.
Editor: Joaquim Agostinho Moreira
DOI: [http://doi.org/10.24927/rce2015.012]

---

Um meio condutor da electricidade caracteriza-se por ter portadores de cargas que se podem mover sob a acção de um campo eléctrico aplicado. O tipo de portadores de carga depende da natureza do meio condutor. Por exemplo, nos metais, são os electrões de condução os responsáveis pelo transporte de carga eléctrica; já nas soluções electrolíticas, são os iões,resultantes da dissociação iónica do electrólito, que transportam a carga, enquanto que nos plasmas, são os electrões e iões os responsáveis pelo transporte.

Em todos os condutores, as cargas eléctricas encontram-se em movimento. Contudo, uma vez que este movimento é desordenado, não há transporte efectivo de carga eléctrica. Para haver corrente, é necessário aplicar um campo eléctrico para orientar o movimento das cargas. Assim sendo, existe uma relação entre a densidade de corrente, 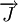$\overrightarrow{J}$, e o campo eléctrico, 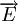$\overrightarrow{E}$. Na maioria dos condutores metálicos, esta relação é de proporcionalidade directa:

$\overrightarrow{J} = \sigma \overrightarrow{E}$

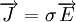
sendo 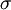$\sigma$ a conductividade eléctrica do metal.

Para descrever os fenómenos físicos que determinam a condução eléctrica, usa-se um modelo clássico, cujos pressupostos são:

1. a rede metálica é constituida por iões que ocupam posições fixas no espaço, e um gás de electrões de condução que se move entre os iões. Os iões são considerados como objectos impenetráveis, de massa muito superior à dos electrões.

2. os electrões de condução colidem apenas com os iões que constituem a rede metálica; entre colisões, os electrões de condução não interactuam entre si nem com os iões da rede metálica.

3. as colisões dos electrões de condução e os iões da rede consideram-se instantâneas, mudando abruptamente a velocidade dos electrões. A direcção da velocidade dos electrões após uma colisão é completamente aleatória, não tendo relação com a velocidade antes da colisão.

4. Em média, o intervalo de tempo entre duas colisões sucessivas é constante - tempo de percurso médio 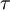$\tau$ - e a probabilidade por unidade de tempo de ocorrer uma colisão é o inverso de $\tau$.

Modelo simplificado de um condutor metálico. As partículas maiores representam os iões da rede metálica e a cheio pode ver-se uma possível trajectória descrita por um electrão de condução. Em pormenor estão representadas a tracejado as possíveis trajectórias que o electrão pode tomar após uma colisão com um ião da rede metálica.

Suponhamos que o metal é formado por um único elemento, de massa atómica 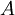$A$. Cada átomo do elemento contribui com 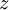$z$ electrões para a condução. Se a densidade do metal for 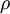$\rho$, o número de electrões de condução por unidade de volume, também designado por densidade de electrões de condução, é dado por:

$n = 6.022 \times 10^{23} \frac{z \rho}{A}$.

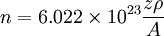Admitamos que os electrões de condução têm velocidade média 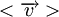$<\overrightarrow{v}>$. A quantidade de carga eléctrica que atravessa a secção recta do condutor por unidade de tempo e de área é a densidade de corrente eléctrica, que é escrita da seguinte forma:

$\overrightarrow{J} = - n e <\overrightarrow{v}>$,

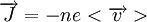sendo 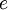$e$ a carga elementar.

A velocidade máxima que o electrão atinge em média entre duas colisões sucessivas pode calcular-se a partir da dinâmica clássica, em que se admite que o electrão está sujeito apenas à força eléctrica. Se 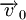$\overrightarrow{v}_0$ é a velocidade do electrão imediatamente após uma colisão, a velocidade que ele adquire num instante 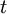$t$, entre as duas colisões sucessivas é:

$\overrightarrow{v} = \overrightarrow{v}_0 - \frac{e \overrightarrow{E} t}{m}$.

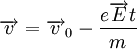Uma vez que a primeira parcela do segundo membro da equação anterior é perfeitamente aleatória, o seu valor médio é zero. Deste modo, a velocidade média com que os electrões se deslocam é:

$<\overrightarrow{v}> = - \frac{e \overrightarrow{E} \tau}{m}$,

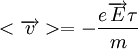em que 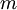$m$ é a massa do electrão. Considerando esta expressão para a velocidade média dos electrões, a relação entre da densidade de corrente e o campo eléctrico, admitindo linearidade, é:

$\overrightarrow{J} = \frac{ n e^2 \tau}{m} \overrightarrow{E}$

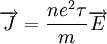
donde se conclui que a condutividade eléctrica do metal é:

$\sigma = \frac{ n e^2 \tau}{m}$.

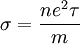Com base na última equação, podemos interpretar o facto da condutividade eléctrica de um metal diminuir com o aumento da sua temperatura. De facto, o aumento de temperatura é consequência do aumento da energia interna do metal, que se traduz por uma agitação térmica com maior amplitude. Assim sendo, a probabilidade por unidade de tempo do electrão colidir com um ião da rede aumenta, pelo que 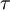$\tau$ diminui.

Apesar da sua simplicidade, este modelo não explica certos aspectos do transporte de carga em metais, por exemplo a magnetoresistência e o efeito termoeléctrico.

---

Criada em 07 de Março de 2011
Revista em 25 de Março de 2011
Aceite pelo editor em 25 de Março de 2011