Referenciais
Referência : Não citável Esta página ainda não foi aprovada.
Autor: João Nuno Tavares e Ângela Geraldo
Editor: Colocar nome do editor
Índice |
Referencial Cartesiano no plano
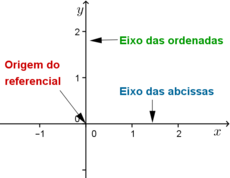
Um referencial cartesiano no plano é um sistema constituído por dois eixos ortogonais (ou seja, dois eixos perpendiculares) - o eixo das abcissas ou eixo dos \(xx\) e o eixo das ordenadas ou eixo dos \(yy\). Ao ponto de intersecção dos dois eixos chamamos de origem.
Um referencial cartesiano no plano serve para estudar geometria plana com ajuda de álgebra, isto é, estudar Geometria Analítica em duas dimensões (2D).
|
A cada ponto \(A\) do plano associamos, de forma unívoca, o par de coordenadas relativas a esse sistema de eixos (ou referencial). \[A \quad \longleftrightarrow \quad (x_A,y_A) \in \mathbb{R}^2\] \(x_A\) diz-se a abcissa e \(y_A\) a ordenada do ponto \(A\). Escrevemos então:
As figuras do plano, tais como, retas, curvas, polígonos, e outros lugares geométricos, podem então ser descritos por equações ou inequações nas variáveis \(x\) e \(y\), onde \(P(x,y)\) designa um ponto genérico desse lugar. |
Referencial Cartesiano no espaço
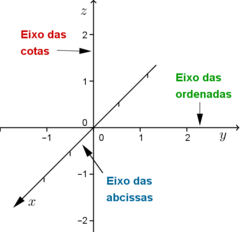
Um referencial cartesiano no espaço é um sistema constituído por três eixos ortogonais (ou seja, três eixos perpendiculares entre si) - o eixo das abcissas, o eixo das ordenadas e o eixo das cotas ou eixo dos \(zz\).
Um referencial cartesiano no espaço serve para estudar geometria espacial com ajuda de álgebra, isto é, estudar Geometria Analítica em três dimensões (3D).
A cada ponto \(A\) do plano associamos, de forma unívoca, o terno de coordenadas relativas a esse sistema de eixos (ou referencial).
\[A \quad \longleftrightarrow \quad (x_A,y_A,z_A) \in \mathbb{R}^3\]
\(x_A\) diz-se a abcissa, \(y_A\) a ordenada e \(z_a\) a cota do ponto \(A\). Escrevemos então:
| \[A(x_A,y_A,z_A)\] |
|---|
As figuras do espaço, tais como, retas, planos, curvas, superfícies, poliedros, e outros lugares geométricos, podem então ser descritos por equações ou inequações nas variáveis \(x\), \(y\) e \(z\), onde \(P(x,y,z)\) designa um ponto genérico desse lugar.
Quadrantes e Octantes
Os eixos de um referencial cartesiano dividem o plano em quatro partes aos quais chamamos de quadrantes, existe por isso quatro quadrantes. A figura seguinte ilustra esse divisão.
| Como se pode verificar pela figura ao lado, no 1º e 4º quadrantes as coordenadas têm o mesmo sinal, ou são ambas positivas(1ºQ) ou ambas negativas (4ºQ). Já no 2º e 3º quadrantes têm sinais diferentes, no 2ºQ as abcissa são negativas e as ordenadas positivas já no 3ºQ é o contrário. |
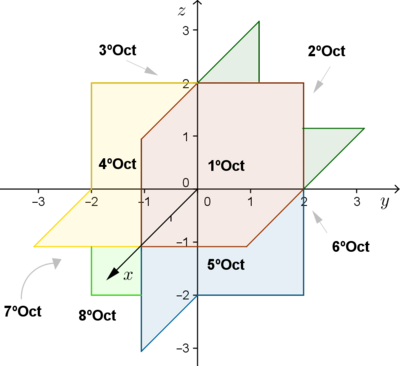
O espaço é também dividido em partes pelos eixos coordenados, às quais chamamos de octantes, existem assim oito octantes. A figura abaixo ilustra essa divisão.
| 1 |