Grafo
Referência : Ribeiro, P. (2012), WikiCiências, 3(06):0628
Autor: Pedro Ribeiro
Editor: Fernando M. A. Silva
Um grafo é uma que representação abstrata de um conjunto de objetos e das relações existentes entre eles. É definido por um conjunto de nós ou vértices, e pelas ligações ou arestas, que ligam pares de nós. Uma grande variedade de estruturas do mundo real podem ser representadas abstratamente através de grafos.
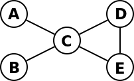
A figura seguinte ilustra um grafo com 5 nós.
Índice |
Conceitos
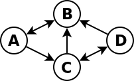
Um grafo é descrito por um par (V,E), onde V é o conjunto de vértices e E o conjunto das arestas que ligam pares de vértices. Um grafo pode ser dirigido ou direcionado, se as arestas tiverem uma direção, ou não dirigido, se as arestas não tiverem direção. A figura seguinte ilustra um grafo dirigido.
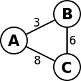
Se as arestas tiverem associado um peso ou custo, o grafo passa a chamar-se de grafo pesado. A figura seguinte ilustra um grafo pesado não dirigido.
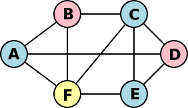
Os nós podem ser de diferente tipos, representados por cores ou etiquetas. Nesse caso, o grafo diz-se colorido. A figura seguinte ilustra um grafo colorido não dirigido.
Quando apenas é admitida no máximo uma aresta entre dois nós, diz-se que o grafo é simples.
Aplicações
Um vasto leque de sistemas naturais ou artificiais pode ser representado através de grafos. Por exemplo, no campo da biologia podemos ter uma cadeia alimentar, com os animais a serem os nós, e as relações de predador-presa entre eles a serem as arestas. Podemos ter também outras estruturas biológicas, tais como uma rede neuronal (ligações entre neurónios) ou uma rede interação entre proteínas. Na sociologia podemos ter uma rede social de amigos com ligações representando amizades. No software podemos ter uma rede representando heranças entre objetos. Num patamar de existência mais física podemos ter grafos representando uma rede de auto-estradas ligando cidades, uma rede elétrica ligando casas, uma rede computadores, ou uma rede de páginas da internet com hiperligações entre si. Muitos mais exemplos poderiam ser dados, mas o essencial é perceber que os grafos são uma representação abstrata muito poderosa e flexível.
Grafos e a Ciência de Computadores
Dada a enorme utilidade dos grafos como representações de conhecimento, existe toda uma área de Ciência de Computadores dedicada ao seu estudo e são inúmeros e muito importantes os algoritmos que manipulam grafos. Um exemplo é o Algoritmo de Dijkstra, que encontra o caminho mais curto entre um nó e todos os outros nós, num grafo pesado. Existem muitos outros algoritmos para outras tarefas tais como maximizar o fluxo entre nós ou encontrar a árvore mínima de suporte.
Do ponto de vista da Programação, um grafo é uma estrutura de dados e existem duas maneiras base de o implementar na prática:
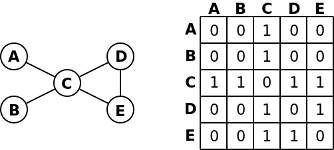
- Matriz de Adjacências: uma matriz de V por V células, onde a célula na linha i e coluna j nos dá informação sobre a ligação entre os nós i e j. Por exemplo, se o grafo não for pesado, a célula podia conter o valor verdadeiro (ou um) quando existisse uma ligação entre i e j e o valor falso (ou zero) quando tal não acontecesse. Se o grafo for pesado, cada célula pode conter um número representando o peso da aresta. A figura seguinte ilustra um grafo não dirigido e a sua correspondente matriz de adjacências.
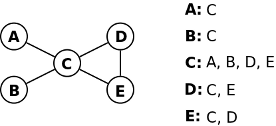
- Lista de Adjacências: um vetor de listas onde a posição i do vetor contém uma lista dos nós aos quais o nó i se encontra ligado. Se o grafo for pesado, cada elemento da lista contém também o peso da ligação. A figura seguinte ilustra um grafo não dirigido e a sua correspondente lista de adjacências.
A matriz permite verificar em tempo constante se uma dada ligação existe ou não. Por oposição, no caso da lista, tal não acontece e é necessário percorrer a lista para saber se um dado nó está ou não ligado. Em contrapartida, se for necessário percorrer todos os nós ligados a um dado nó, a lista é mais eficiente, pois permite percorrer apenas os nós ligados, e não andar a percorrer toda uma linha da matriz, verificando se a ligação existe ou não.
Saber Mais
- Página Web: http://www.mat.uc.pt/~alma/escolas/pontes/ O problema das 7 pontes de Königsberg. Acedido a 29/05/2012.
- Página Web: http://mathworld.wolfram.com/Graph.html Os grafos no Wolfram MathWorld, um dos maiores repositórios de Matemática da Web. Acedido a 29/05/2012. (em inglês)
Criada em 29 de Maio de 2012
Revista em 29 de Maio de 2012
Aceite pelo editor em 02 de Junho de 2012