As simetrias nas calçadas de Lisboa
Referência : Cannas da silva, A., Rodrigues, J. F., Nápoles, S. M., (2024) As simetrias nas calçadas de Lisboa, Rev. Ciência Elem., V12(3):025
Autores: Ana Cannas da Silva, José Francisco Rodrigues e Suzana Metello de Nápoles
Editor: João Nuno Tavares
DOI: [https://doi.org/10.24927/rce2024.025]

Resumo
Através do reconhecimento de frisos e padrões nas calçadas de Lisboa, pretende-se neste artigo abordar os 24 tipos de simetria plana, caracterizando-as e revelando o seu potencial cultural e didático.
A Calçada Portuguesa é uma forma de arte portuguesa, que está hoje espalhada por todo o país e por todo o mundo, do Brasil a Macau, passando por África. Esta expressão cultural é uma herança histórica da cultura e da tecnologia de empedramento das vias e mosaicos romanos, que se renovou em Portugal na renascença nos reinados de D. João II e de D. Manuel.
A primeira das calçadas decorativas, hoje conhecidas por Calçadas Portuguesas, terá sido feita em Lisboa em 1842. Eusébio Pinheiro Furtado, oficial de engenharia e então o governador do Castelo de São Jorge, mandou fazer uma calçada num dos acessos ao castelo por presos da Cadeia do Limoeiro. Esse pavimento com um traçado simples, a preto e branco usando calcário e basalto, teve grande sucesso, servindo de exemplo à pavimentação de toda a área da Praça do Rossio, numa extensão de 8 712 m², que ficou concluída em 1849 com um padrão da autoria daquele engenheiro militar.

Esse padrão, com ondas pretas e brancas, tornou-se icónico e ficou conhecido como Mar Largo, em homenagem aos descobrimentos Portugueses, evocando a expressão camoniana5 dos versos de Os Lusíadas (IV.66):
Manuel, que a Joane sucedeu
No Reino e nos altivos pensamentos,
Logo tomou do Reino cargo,
Tomou mais a conquista do mar largo.
O Mar Largo do Rossio foi removido em 1919 e parcialmente reposto em 1976, tendo sido restabelecido na sua forma atual em 2001. Entretanto, o Mar Largo esteve presente na Exposição Universal de Paris em 1900 e atravessou rapidamente o Atlântico calçando o Largo de São Sebastião em Manaus, em 1901, e a marginal de Copacabana, no Rio de Janeiro em 1905, dando lugar ao atual calçadão carioca em 1970. Surge atualmente em vários locais, em Portugal e no Mundo, como, por exemplo, em Cascais ou na Nazaré e na Ilha de Moçambique ou em Macau, no Largo do Senado até à Igreja de São Domingos.
A simetria sempre fascinou a humanidade, aparecendo na arquitetura, nas artes decorativas, nas engenharias e nas ciências. Há milhares de anos que os padrões planos são utilizados no dia-a-dia em artefactos, tecidos ou pavimentos, seja nas formas primitivas da civilização, seja nas formas mais avançadas. Por exemplo, na Idade Média, a arte islâmica criou formas geométricas com simetrias elaboradas, alcançando no século XIII e XIV, nos caleidoscópios e nos mosaicos da Alhambra, em Granada, o conjunto completo dos 17 padrões cristalográficos do plano.
O conceito de simetria foi introduzido nas ciências, e em particular na matemática, no século XIX. A sua associação aos grupos de transformação na geometria, em 1869, está associada a Camille Jordan, e o estudo das simetrias na cristalografia, aos trabalhos do matemático Artur Schönflies, que, em 1891, conduziram à catalogação completa dos 230 grupos de simetria espacial, em colaboração com o mineralogista Evgraf Fedorov, que também efetuou a primeira identificação dos grupos cristalográficos no plano e concluiu serem exatamente 17.
Mas o que significa ter simetria? Em linguagem corrente, dizemos que uma figura é simétrica (do grego antigo sum metria) se possui uma simetria axial. Mais geralmente, podemos dizer que uma figura ainda é simétrica mesmo quando não tem eixos de simetria, desde que exista uma transformação geométrica, como uma rotação ou uma reflexão, que a deixa globalmente invariante, isto é, podem alguns ou todos os pontos da figura mudar de posição mas a figura, como um todo, não apresenta modificações em relação à forma inicial.
A definição matemática de simetria recorre ao conceito de grupo, mas não necessitamos dele para caracterizar os quatro tipos de simetria relevantes à compreensão dos padrões e os frisos no plano das calçadas. São eles:
- Simetria por reflexão (espelhos);
- Simetria por rotação (girações);
- Simetria por reflexão deslizante (cruzamentos);
- Simetria só por translação (admirações).
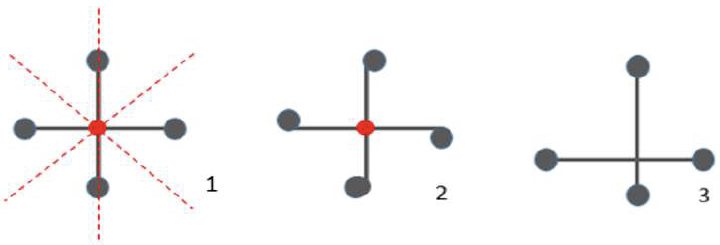
Tal como se usam os algarismos para exprimir números e símbolos para representar operações matemáticas, usaremos uma notação introduzida por Conway nos anos 1980’s, para denotar os tipos de simetrias, atribuindo uma assinatura simbólica a cada uma delas. Assim, uma estrela * é usada para indicar uma simetria de espelho, e para a assinatura do tipo da simetria da letra H, que tem dois eixos de simetria que se cruzam num ponto, escrevemos *2.
Os algarismos 2, 3, 4, … são usados para simbolizar a ordem da rotação em torno de cada centro de simetria. Por exemplo, a assinatura do tipo de simetria da cruz 2 da FIGURA 2 é simplesmente 4 (=360°/90°).
O símbolo X denota uma reflexão deslizante, que, juntamente com as reflexões e as rotações, devem ser contabilizadas em prioridade sobre as translações.
O símbolo O denota uma simetria só por translação. Um padrão do tipo O é um padrão que não apresenta nem espelhos, nem girações, nem cruzamentos, e apenas apresenta translações.





Para além da pioneira e icónica calçada do Mar Largo, Lisboa tem várias outras praças e múltiplas ruas pavimentadas com a Calçada Portuguesa. Para além da Praça dos Restauradores, cujo padrão com a assinatura 4 4 2 foi desenhado pelo arquiteto e ilustrador João Abel Manta, a Praça do Município foi repavimentada em 1997/1998 com uma calçada desenhada pelo pintor e artista plástico Eduardo Nery, com uma simetria do tipo * 4 4 2.

Em 1924 o matemático George Pólya redescobriu os 17 grupos de simetria bidimensionais, também chamados grupos cristalográficos no plano ou de papéis de parede, encontrados por Fedorov em 1891.
Estes têm uma complexidade intermédia entre os 7 grupos dos frisos, cujos padrões de simetria em forma de faixa incluem necessariamente o símbolo ∞ na assinatura, e os grupos espaciais de simetria nas dimensões 3 e 4, que são, respetivamente 219 (ou 230 se as cópias quirais forem consideradas distintas) e 4783. O quadro abstrato da topologia algébrica permitiu, nos anos 1980’s, dar uma explicação geométrica para a existência de exatamente 24 tipos de simetria planar[5], que chamaremos Teorema Mágico (FIGURA 7), sendo 17 papéis de parede e 7 frisos.
Os frisos encontram-se nas artes decorativas de várias civilizações. Com efeito, com as nossas pegadas podemos estampar facilmente os sete tipos de frisos, todos eles existindo já nas calçadas de Lisboa. Alguns são antigos, outros mais recentes como o padrão ∞ X, colocado na Praça Duque de Saldanha em 2017.
Uma das autoras, tendo observado mais de duzentas calçadas públicas em Portugal desde 2005, ano em que o matemático e professor da Universidade de Princeton (EUA) ministrou um curso sobre simetria em Lisboa, lançou o projeto Simetria Passo a Passo[6], que contou com o apoio da Fundação Calouste Gulbenkian e, com a colaboração de dois estudantes do Instituto Superior Técnico, procedeu a um primeiro levantamento sistemático das calçadas simétricas, tendo proposto, em 2010, uma Rota da Simetria para Lisboa.
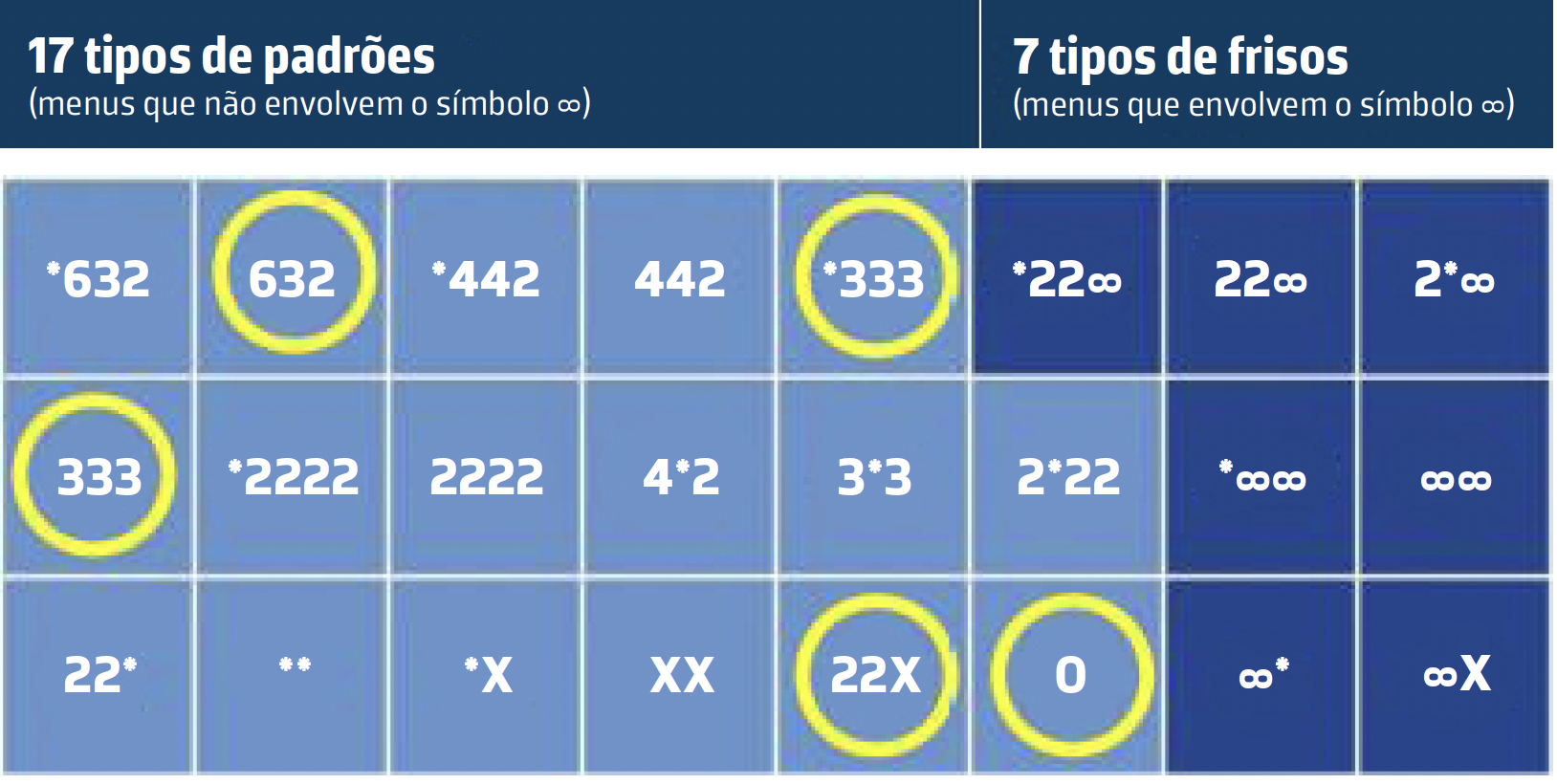
Em 2006, a Câmara Municipal de Lisboa e a Sociedade Portuguesa de Matemática assinaram um protocolo de colaboração para divulgar e completar os tipos de simetria existentes nas calçadas de Lisboa. Apesar dos 7 tipos de frisos já ter sido completado, ainda não se conhecem os 5 padrões indicados na FIGURA 7.

As simetrias planas na cultura portuguesa não aparecem só nas calçadas, mas também, por exemplo, nos azulejos. A riqueza visual e didática da simetria constitui um tema de relevante para a divulgação da matemática e para o ensino, fazendo parte dos novos programas do ensino básico.

A descrição de um DVD Simetria, apresentação dinâmica[7], produzido em 2009 pela associação Atractor, baseia-se na ideia da classificação dos padrões duplamente periódicos no plano inspirada no tratamento dos matemáticos M. MacBeath e W. Thurston que conduziu ao referido Teorema Mágico[8]. Esse DVD é ilustrado com azulejos portugueses e mostra animações da produção de frisos e padrões com os 24 carimbos da FIGURA 11.

A associação Atractor produziu e disponibiliza em acesso livre o programa GeCLa, acessível a alunos de vários graus de ensino, que é capaz de gerar frisos e padrões e classificar as simetrias do plano. Este instrumento é, portanto, um poderoso meio de, dando largas à criatividade artística de cada um, em particular dos jovens, ajudar a promover a concursos para a construção de frisos e padrões e completar as 24 simetrias, não só nas calçadas de Lisboa, mas também pelas ruas e praças do resto do país.
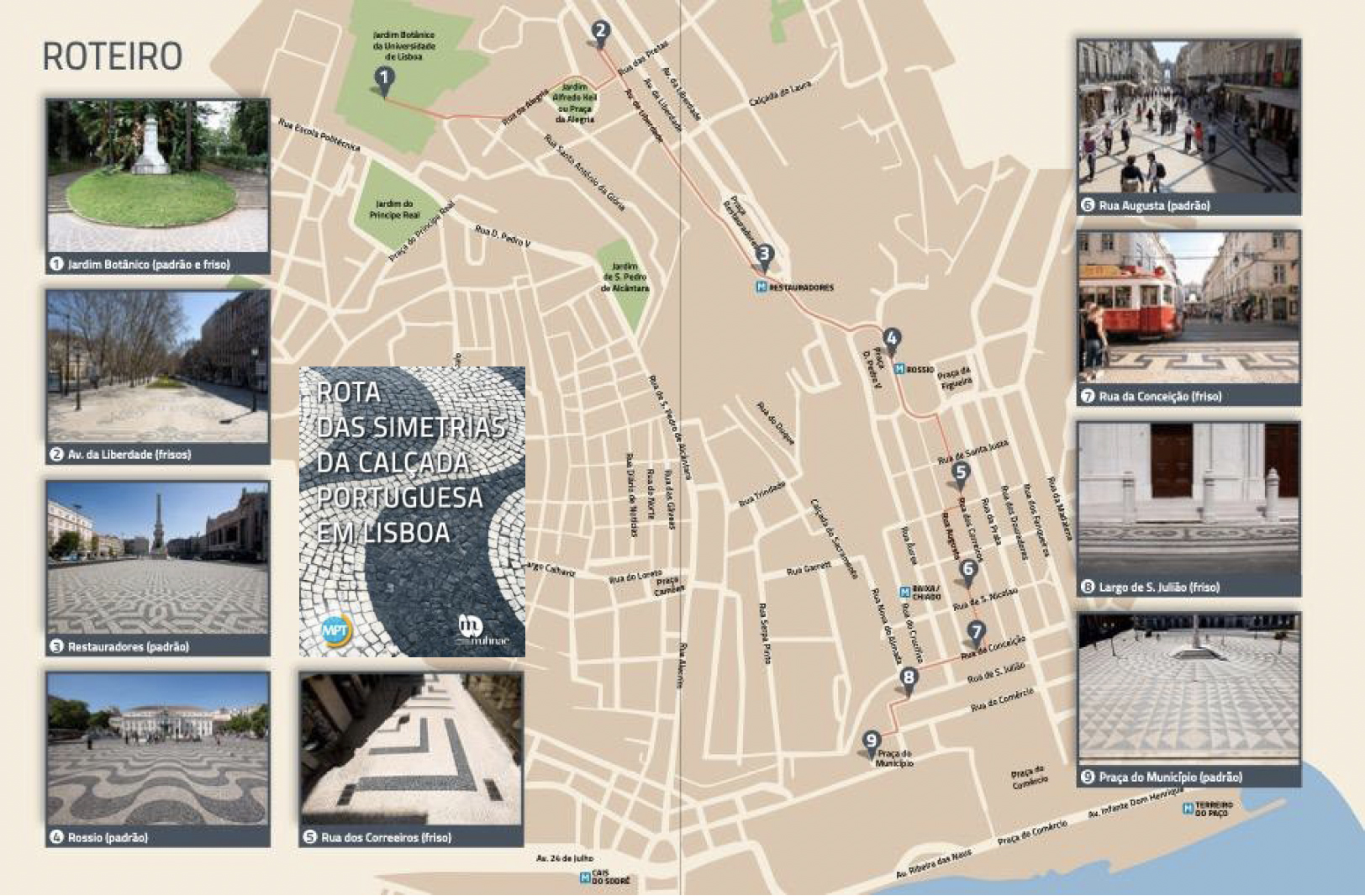
No âmbito da celebração do tema Matemática do Planeta Terra, uma iniciativa lançada no quadro da IMU (International Mathematical Union), que envolveu em 2013 várias associações e instituições em Portugal e foi apoiada pela Comissão Nacional de Matemáticas e pela Comissão Nacional da UNESCO, o Museu Nacional de História Natural e da Ciência da Universidade de Lisboa organizou uma série de ações e, seguindo a sugestão do projeto Simetria Passo a Passo, em particular, lançou em junho desse ano uma série de visitas guiadas com uma Rota das simetrias das calçadas de Lisboa, com um percurso com nove calçadas, partindo da calçada do Jardim Botânico e terminando na Praça do Município, passando pelas Praças dos Restauradores e do Rossio.

Essas visitas guiadas, que tiveram o apoio do Ciência Viva e da Câmara Municipal de Lisboa, mostravam e explicavam as assinaturas dos padrões dessas nove calçadas e relatavam as caraterísticas geológicas de Lisboa, evocando a ligação aos cristais através das simetrias matemáticas e anunciando o Ano Internacional da Cristalografia que decorreu em 2014.
Em 2017 foi constituída a Associação da Calçada Portuguesa, impulsionada pela Câmara Municipal de Lisboa, com o desígnio de proteger, promover, valorizar e a internacionalizar a Calçada Portuguesa.
Agradecimentos.
Os autores agradecem aos fotógrafos João Ferrand e Ernesto Matos a autorização da reprodução das imagens de Lisboa (nas FIGURAS 3, 4, 5 e 6) e de Aveiro (na FIGURA 6), respetivamente.
ANEXO
O roteiro das simetrias de nove calçadas em Lisboa nas visitas guiadas organizadas pelo Museu Nacional de História Natural e da Ciência da Universidade de Lisboa, participaram nas celebrações da Matemática do Planeta Terra em 2013.
Referências
- ↑ CANNAS DA SILVA, A., Simetria Passo a Passo: Calçadas de Portugal, Edições CTT. 2016.
- ↑ CANNAS DA SILVA, A., Simetria Passo a Passo: Calçadas de Portugal, Edições CTT. 2016.
- ↑ CANNAS DA SILVA, A., Simetria Passo a Passo: Calçadas de Portugal, Edições CTT. 2016.
- ↑ CANNAS DA SILVA, A., Simetria Passo a Passo: Calçadas de Portugal, Edições CTT. 2016.
- ↑ CONWAY J. H. et al., The Symmetry of Things, A. K. Peters. 2008.
- ↑ CANNAS DA SILVA, A., Simetria Passo a Passo: Calçadas de Portugal, Edições CTT. 2016.
- ↑ RODRIGUES, J. F., A Matemática e o Planeta Terra, Boletim da SPM 76, pp.1-32. 2018.
- ↑ CONWAY J. H. et al., The Symmetry of Things, A. K. Peters. 2008.
- ↑ CANNAS DA SILVA, A., Simetria Passo a Passo: Calçadas de Portugal, Edições CTT. 2016.
Criada em 25 de Agosto de 2024
Revista em 28 de Agosto de 2024
Aceite pelo editor em 15 de Outubro de 2024

