Solitões

Da WikiCiências
Share/Save/Bookmark
Revisão das 15h02min de 17 de março de 2021 por Admin (discussão | contribs)

(dif) ← Revisão anterior | Revisão actual (dif) | Revisão seguinte → (dif)
Ir para: navegação, pesquisa

Referência : Gomes, C., (2021) Solitões, Rev. Ciência Elem., V9(1):004
Autor: Cláudio Gomes
Editor: José Ferreira Gomes
DOI: [https://doi.org/10.24927/rce2021.004]
PDF Download

Resumo

Um solitão é um tipo de onda que resulta de um equilíbrio entre o efeito de não linearidade e o de dispersão/difração, sendo que mantém a sua forma e velocidade ao longo da trajetória, e preserva as suas características após colisão com outro solitão, a menos de uma mudança de fase.


Em agosto de 1834, o engenheiro escocês John Scott Russell observava uma embarcação em movimento no estreito Canal da União, perto de Edimburgo na Escócia. Ao longo dessa trajetória, formou-se uma ligeira elevação de água na frente da proa. E quando esta pequena embarcação parou, Russell verificou que essa onda na proa se propagava sempre em frente mantendo a sua forma e velocidade sem aparente atenuação. Esta situação contrastava com a experiência de senso comum de quando se atira uma pedra num lago, por exemplo, na qual a onda formada vai perdendo amplitude ao longo do seu percurso. A este tipo de onda designou “onda de translação”. Bastante intrigado com esse fenómeno, procurou sistematizar a informação num artigo dez anos mais tarde à primeira observação, tendo concluído quatro importantes características[1]:

  1. São ondas que apresentam a forma de uma secante hiperbólica (FIGURA 1) (notemos que \(sech\left ( x \right )=\frac{2}{e^{x}+e^{-x}}\))
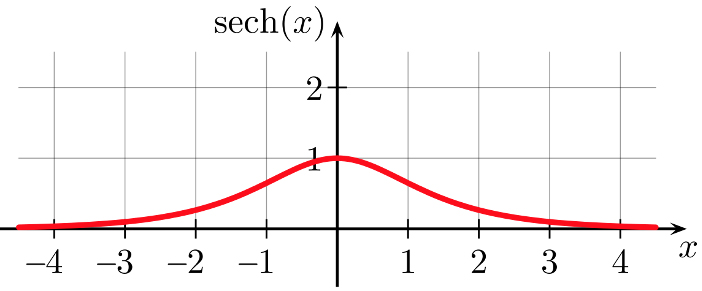
    FIGURA 1. Representação gráfica de uma função secante hiperbólica.

  2. Uma quantidade considerável de água inicial pode produzir duas ou mais “ondas de translação” próximas e independentes ao longo do tempo;
  3. Após colisões, preservam as suas características iniciais;
  4. Num canal superficial de altura h em relação ao fundo, uma “onda de translação” de altura \(A\) percorre a sua trajetória com velocidade igual a \(\sqrt{g\left ( A+h \right )}\), em que \(g\) é a aceleração gravitacional. Devido à não linearidade da onda, essa fórmula mostra que ondas de maior amplitude apresentam maior velocidade.


Passaram-se anos, após esta observação, até que houvesse interesse da comunidade científica neste fenómeno. Assim, em 1871, Boussineqe , em 1876, Rayleigh produziram trabalhos que mostraram que a forma permanente da onda se devia a uma compensação entre o efeito do aumento da velocidade local da onda em função da altura desta e o efeito da diminuição da amplitude associada à dispersão.

Todavia, somente em 1895, os neerlandeses Diederick Korteweg e Gustav de Vries derivaram uma equação diferencial não linear às derivadas parciais, conhecida como Korteweg- de Vries (KdV), cuja solução é um solitão, e que pode descrever o fenómeno observado por Russell[2]:

\(\frac{d\phi }{dt}+\frac{d^{3}\phi}{dx^{3}}+6\phi\frac{d\phi}{dx}=0\),

onde o primeiro termo representa a variação temporal da onda que é dada pelo equilíbrio entre a dispersão patente na aceleração da variação espacial do segundo termo e a não linearidade expressa no terceiro termo. Esta equação tem como solução uma onda cnoidal (FIGURA 2) com a seguinte forma: \(\phi\left ( x,t \right )=\frac{\nu}{2}sech^{2}\left ( \frac{\sqrt{\nu}}{2}\left ( x-x_{0}-\nu t \right ) \right )\), onde \(\nu\) é a velocidade de propagação da onda.


FIGURA 2. Representação gráfica de diferentes ondas a propagar-se segundo um dado eixo/direção: A) Onda Linear. B) Onda Cnoidal. C) Onda Solitária.

De facto, a não linearidade é responsável por pontos diferentes da onda propagarem-se com velocidade diferente dependente da sua altura, ao passo que a dispersão é responsável pelo espraiamento da onda, e por diferentes comprimentos de onda viajarem a velocidades diferentes.

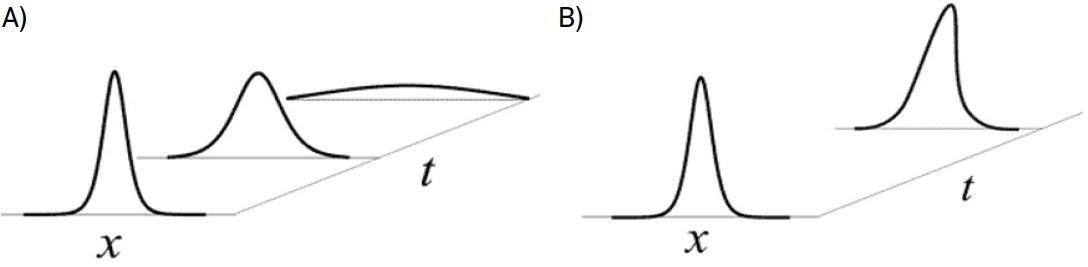
Posteriormente, em 1965 surgem soluções numéricas de solitões por Norman Zabusky e Martin Kruskal e é nesta altura que o termo solitão é inventado[3]. Segundo estes, um solitão é um pulso coerente de larga amplitude ou uma onda solitária muito estável, sendo a solução de uma equação de onda, e cuja forma e velocidade não são alteradas pela colisão com outras ondas solitárias. Notemos, contudo, que após a colisão entre dois solitões, pode haver uma mudança na fase na função de onda.


FIGURA 3. A) Diminuição da amplitude de uma onda fruto da dispersão ao longo do tempo. B) Evolução temporal de uma onda não-linear, em que pontos diferentes da onda têm velocidades diferentes.

De facto, esta equação diferencial não só descreve as ondas observadas por Russell, como também pode ser aplicada a inúmeros outros problemas, como a modelação da pressão sanguínea, ou da Grande Mancha de Júpiter ou até da matéria escura nas galáxias e enxames de galáxias, para citar alguns.

Mas o seu ramo de aplicações não termina aqui. Existem outras equações cujas soluções podem ser ondas solitárias, como é o caso da equação de Burges utilizada em contextos de mecânica de fluidos, acústica não linear ou fluxo de trânsito, e que a uma dimensão espacial é escrita como[4], [5]:

\(\frac{\partial \psi }{\partial t}+\psi \frac{\partial \psi }{\partial x}=\sigma \frac{\partial ^{2}\psi }{\partial x^{2}}\),

em que \(\sigma\) é o coeficiente de difusão (ou viscosidade cinemática como no artigo original).

Outro exemplo de uma equação cuja solução resulta na descrição de um solitão é o da equação de Schrödinger com um termo potencial quadrático, a denominada equação de Schrödinger não linear, que, após uma redefinição de variáveis, pode apresentar-se na seguinte forma[6], [7]:

\(i\frac{\partial q}{\partial \zeta }\pm \frac{1}{2}\frac{\partial ^{2}q}{\partial \lambda ^{2}}+\left | q \right |^{2}q=0\)

em que os sinais + e – correspondem às dispersões anómala e normal, respetivamente. Daqui podem surgir solitões óticos claros e escuros, como apresentados na FIGURA 4. Em particular, este tipo de solitões ocorrem em condensados de Bose-Einstein em que a maioria dos átomos ao arrefecer apresentam uma sobreposição dos seus comprimentos de onda individuais e comportam-se identicamente[8].


FIGURA 4. Representação gráfica de solitões claro (“ilha que se propaga”) e escuro (“depressão/ausência de luz no continente”) em condensados de Bose-Einstein.

Na realidade, em Ótica Não Linear existem muitos exemplos de ondas solitárias, desde ondas envelope dispersivas de campos elétricos em fibras óticas, a pulsos óticos em arrays e cristais fotorrefrativos[9]. Em particular, quando o efeito da não linearidade é compensado pela difração diz-se que temos ondas solitárias espaciais, ao passo que quando a não linearidade é balanceada pela dispersão diz-se que as ondas solitárias são temporais. Existe, todavia, um terceiro caso: as ondas solitárias espácio-temporais em materiais não lineares de segunda ordem, em que simultaneamente existe um fenómeno de difração pela modulação de auto-foco e um de dispersão por modulação em fase[10].

Também existem solitões topológicos em modelos de teoria de cordas quânticas e de supergravidade, como em D-branas e NS-branas, ou em defeitos em paredes de domínio e cordas cósmicas.

É também muito relevante referir-se que as ondas solitárias, e os solitões, são ubíquos na Natureza e nas nossas vivências comuns. Por exemplo, podemos produzir ondas solitárias nos canais de lava-pés ao lado de piscinas, ou podemos encontrar outros exemplos nos tsunamis e nos furacões. As galáxias espirais são um exemplo de ondas solitárias em vértice, isto é, podemos imaginar um cone, em que o disco galático assenta na base, e o movimento de rotação da galáxia preserva as características da mesma. Na biologia, por exemplo, os golfinhos produzem anéis de ar debaixo de água que se propagam mantendo as suas características iniciais. Uma aplicação humana antiga são os anéis de fumo produzidos por tribos de índios como forma de comunicação a longa distância.

Assim, apesar de serem soluções especiais, as ondas solitárias e os solitões são fenómenos muito comuns na Natureza.

Referências

  1. ↑ RUSSELL, J.S., Report on Waves. in Report of the 14th Meeting of the British Association for the Advancement of Science, 311–390. 1844.
  2. ↑ DE VRIES, G. & KORTEWEG, D.J., On the Change of Form of Long Waves Advancing in a Rectangular Canal, and on a New Type of Long Stationary Waves, Philosophical Magazine, 39, 422–443. 1895.
  3. ↑ ZABUSKY, N. J. & KRUSKAL, M.D., Interaction of “Solitons” in a Collisionless Plasma and the Recurrence of Initial States, Physical Review Letters, 15, 240–243. 1965.
  4. ↑ SCOTT, A.C., Encyclopedia of Nonlinear Science, Routledge, Taylor & Francis Group, New York, NY, 2005.
  5. ↑ EMOISSENEt, M., Waves Called Solitons: Concepts and Experiments, 3rd edition, Springer-Verlag, Berlin, Germany.
  6. ↑ SCOTT, A.C., Encyclopedia of Nonlinear Science, Routledge, Taylor & Francis Group, New York, NY, 2005.
  7. ↑ EMOISSENEt, M., Waves Called Solitons: Concepts and Experiments, 3rd edition, Springer-Verlag, Berlin, Germany.
  8. ↑ ZABUSKY, N.J. & PORTER, M.A., Scholarpedia, 5, (8): 2068. 2010.
  9. ↑ LIU, X. et al. Generation of Optical Spatiotemporal Solitons, Physical Review Letters, 82, (23): 4631–4634. 1999.
  10. ↑ ZABUSKY, N.J. & PORTER, M.A., Scholarpedia, 5, (8): 2068. 2010.

Criada em 21 de Julho de 2020
Revista em 21 de Dezembro de 2020
Aceite pelo editor em 15 de Março de 2021

Obtida de "https://wikiciencias.casadasciencias.org/wiki/index.php?title=Solitões&oldid=29512"