Ciclos termodinâmicos e rendimentos de máquinas térmicas
Referência : Lage, E., (2020) Ciclos termodinâmicos e rendimentos de máquinas térmicas, Rev. Ciência Elem., V8(1):014
Autor: Eduardo Lage
Editor: José Ferreira Gomes
DOI: [http://doi.org/10.24927/rce2020.014]

As origens da Termodinâmica coincidem com o dealbar da revolução industrial no início do sec. XIX. Essa coincidência não é fortuita – na verdade, as primeiras máquinas que vieram a substituir o esforço humano funcionavam na base da conversão de calor em trabalho, levantando logo a questão do seu rendimento: quantos joules posso obter a partir de uma caloria? O primeiro grande desenvolvimento deve-se a James Joule que reconheceu, em 1843, não só que qualquer trabalho pode ser integralmente convertido em calor como estabeleceu as bases para o Primeiro Princípio da Termodinâmica: num sistema isolado, a energia total conserva-se. O segundo grande passo deve-se a Lord Kelvin que, em 1851, especulou não ser possível converter integralmente calor em trabalho, um resultado que viria a fundamentar o importante conceito de entropia introduzido, em 1865, por Rudolf Clausius, e a estabelecer o Segundo Princípio da Termodinâmica: num sistema isolado, a entropia não pode decrescer. Estes dois Princípios balizam completamente a Termodinâmica Clássica e permitem responder à questão: qual o rendimento máximo de uma máquina térmica?
Para responder à questão, consideremos o esquema genérico de funcionamento de uma máquina térmica (FIGURA 1).
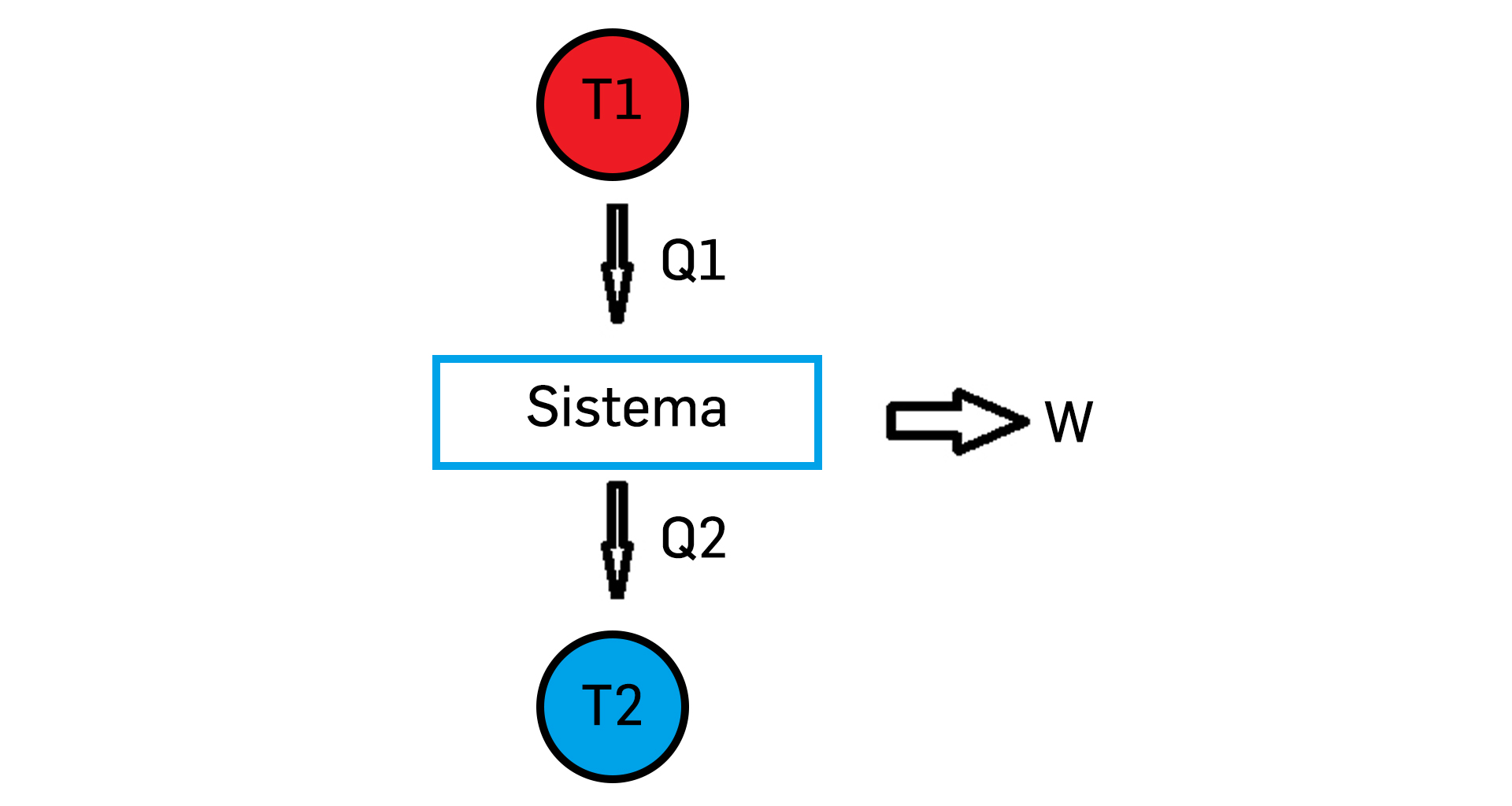
O sistema, que pode ser um gás ou, mais genericamente, um fluido, executa um ciclo regressando ao estado inicial, pelo que não há variação da sua energia interna ou da sua entropia (ver "Introdução à Termodinâmica"). Durante o ciclo, o sistema recebe uma quantidade de calor \(\left ( Q_{1} \right )\) da fonte quente (temperatura \(T_{1}\), realiza trabalho \(\left ( W \right )\) e cede calor \(\left ( Q_{2} \right )\) à fonte fria (temperatura \(T_{2}< T_{1}\)). Então, pelo Primeiro Princípio, é:
\(Q_{1}=Q_{2}+W\)
Fontes e sistema constituem um conjunto isolado. Pelo Segundo Princípio, a entropia do conjunto não pode diminuir. Ora, a fonte quente, cedendo calor, apresenta uma diminuição de entropia igual a \(-\frac{Q_{1}}{T_{1}}\), enquanto a fonte fria, recebendo calor, tem um aumento de entropia igual a \(\frac{Q_{2}}{T_{2}}\). Para o conjunto, deve, então, ser:
\(\Delta S=-\frac{Q_{1}}{T_{1}}+\frac{Q_{2}}{T_{2}}\geq 0\Leftrightarrow \frac{Q_{2}}{Q_{1}}\geq \frac{T_{2}}{T_{1}}\)
O rendimento da máquina é definido por \(\eta =\frac{W}{Q_{1}}\), i.e., quantos joules de trabalho podem ser obtidos a partir de um joule de calor da fonte quente. Das equações anteriores, obtém-se:
\(\eta =\frac{W}{Q_{1}}=1-\frac{Q_{2}}{Q_{1}}\leq 1-\frac{T_{2}}{T_{1}}\)
Nestas expressões, as igualdades só se verificam se o ciclo for reversível. O resultado obtido é muito importante: por um lado, ele é independente da natureza do sistema ou das fontes; por outro lado, fornece um majorante para o rendimento de qualquer máquina térmica.
Invertendo o ciclo, a máquina funciona como um frigorífico, tal como esquematizado na FIGURA 2. Num ciclo, é retirado calor \(\left ( Q_{2} \right )\) da fonte fria, com realização de trabalho \(\left ( W \right )\) sobre o sistema e passando calor \(\left ( Q_{1} \right )\) para a fonte quente. Usando, de novo, os Princípios da Termodinâmica, obtém-se:
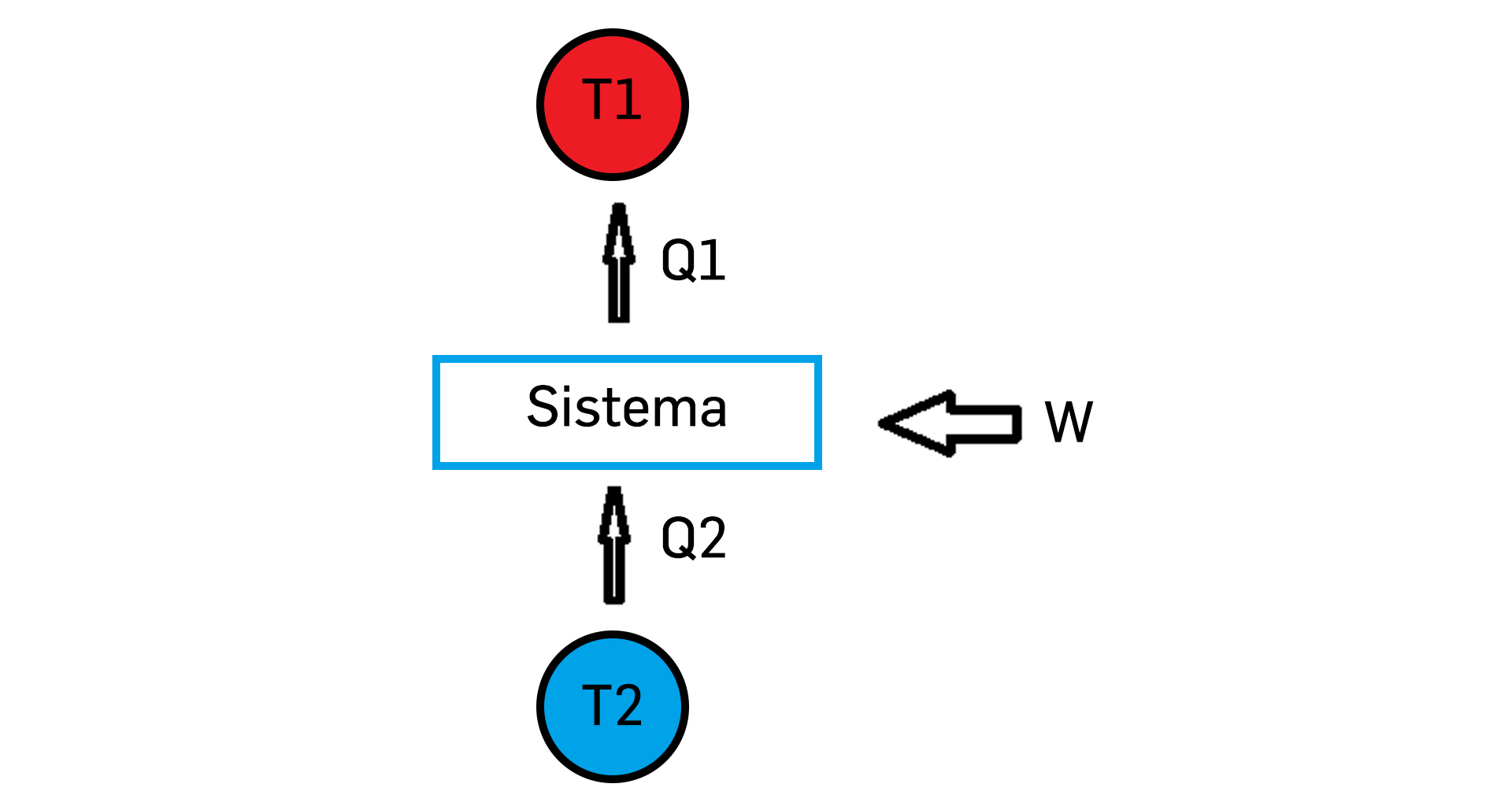
\(Q_{1}=W+Q_{2}\)
\(\Delta S=\frac{Q_{1}}{T_{1}}-\frac{Q_{2}}{T_{2}}\geq 0\Leftrightarrow \frac{Q_{2}}{Q_{1}}\leq \frac{T_{2}}{T_{1}}\)
O rendimento da máquina é, muitas vezes, definido por \(\eta =\frac{Q_{2}}{Q_{1}}\), i.e., quantos calorias se podem extrair da fonte fria por cada caloria transferida para a fonte quente (esta, nos frigoríficos caseiros, é a atmosfera). Tem-se, então \(\eta =\frac{T_{2}}{T_{1}}\).
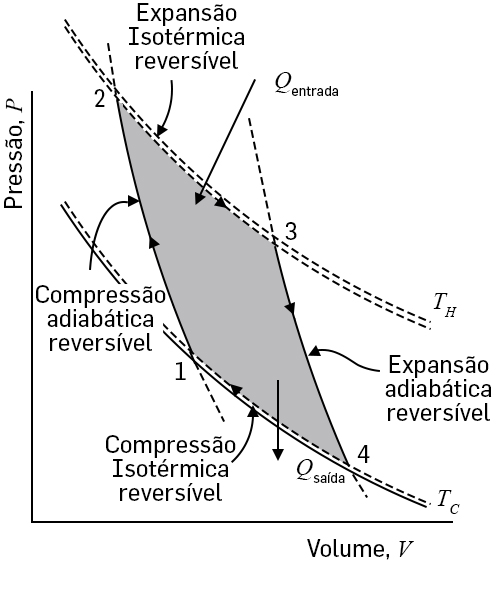
Analisemos, agora, com algum pormenor o ciclo de Carnot para uma máquina térmica. O ciclo aplica-se a um gás submetido a expansões/compressões, isotérmicas e adiabáticas como se mostra no diagrama \((p,V)\) da FIGURA 3. Partindo do ponto (estado) 1, à temperatura inferior \(T_{2}\), o gás é comprimido adiabaticamente (não troca calor) até atingir o ponto 2, à temperatura superior \(T_{1}\). A seguir, é expandido isotermicamente até atingir o ponto 3, onde abandona o contacto com a fonte quente e passa a ser expandido adiabaticamente até atingir a temperatura \(T_{2}\), no ponto 4. Finalmente, uma compressão isotérmica, fá-lo regressar ao ponto inicial 1. O trabalho realizado pelo sistema é \(W=\int dVp\left ( V,T \right )\), onde o integral é calculado ao longo das linhas referidas \(1\rightarrow 2\rightarrow 3\rightarrow 4\rightarrow 1\), sendo numericamente igual à área sombreada, no interior do ciclo. É óbvio que \(W>0\): a contribuição positiva na evolução \(2\rightarrow 3\) é superior à contribuição negativa no trajeto \(4\rightarrow 1\); do mesmo modo, a contribuição positiva no trajeto \(3\rightarrow 4\) não é inferior à contribuição negativa \(1\rightarrow 2\) (para um gás perfeito, estas últimas contribuições anulam-se mutuamente porque, sendo as evoluções adiabáticas, o trabalho iguala a variação da energia interna e esta só depende da temperatura).
Há, porém, uma outra representação do ciclo onde o trabalho é facilmente calculado. Na FIGURA 4, o ciclo é representado num diagrama temperatura-entropia, i.e., diagrama \((T,S)\) onde as isotérmicas são linhas horizontais e as adiabáticas são linhas verticais, isto é, o ciclo é um rectângulo. Usando as leis da termodinâmica, a variação genérica da energia interna é: \(dU=-pdV+TdS\). Integrando ambos os membros ao longo de um ciclo, é \(\int dU=0\) porque o sistema regressa ao estado inicial (recorde-se que a energia interna é uma função de estado). Então:
\(W=\int dVp\left ( V,T \right )=\int dST\)
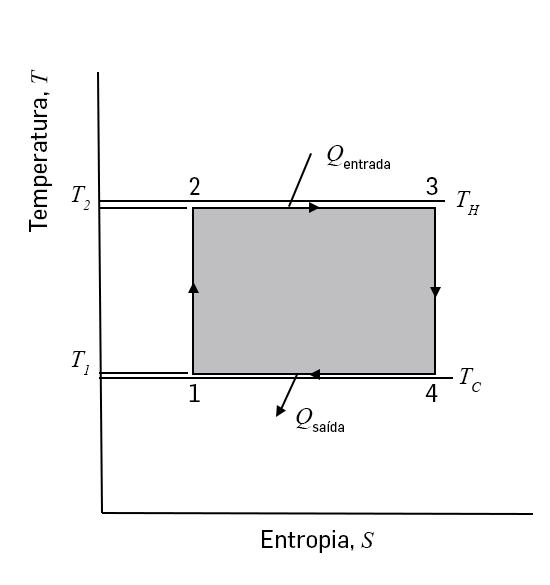
Quer dizer, a área no interior do ciclo na FIGURA 3 é igual à área no interior do ciclo da FIGURA 4. Assim:
\(W=T_{1}\left ( S_{3}-S_{2} \right )-T_{2}\left ( S_{4}-S_{1} \right )=\left ( T_{1}-T_{2} \right )\left ( S_{3}-S_{2} \right )\)
onde a última igualdade resulta de ser \(S_{1}=S_{2}\) e \(S_{3}=S_{4}\). Por outro lado, o calor retirado da fonte quente é \(Q_{1}=T_{1}\left ( S_{3}-S_{2} \right )\), pelo que o rendimento do ciclo é:
\(\eta =\frac{W}{Q_{1}}=1-\frac{T_{2}}{T_{1}}\)
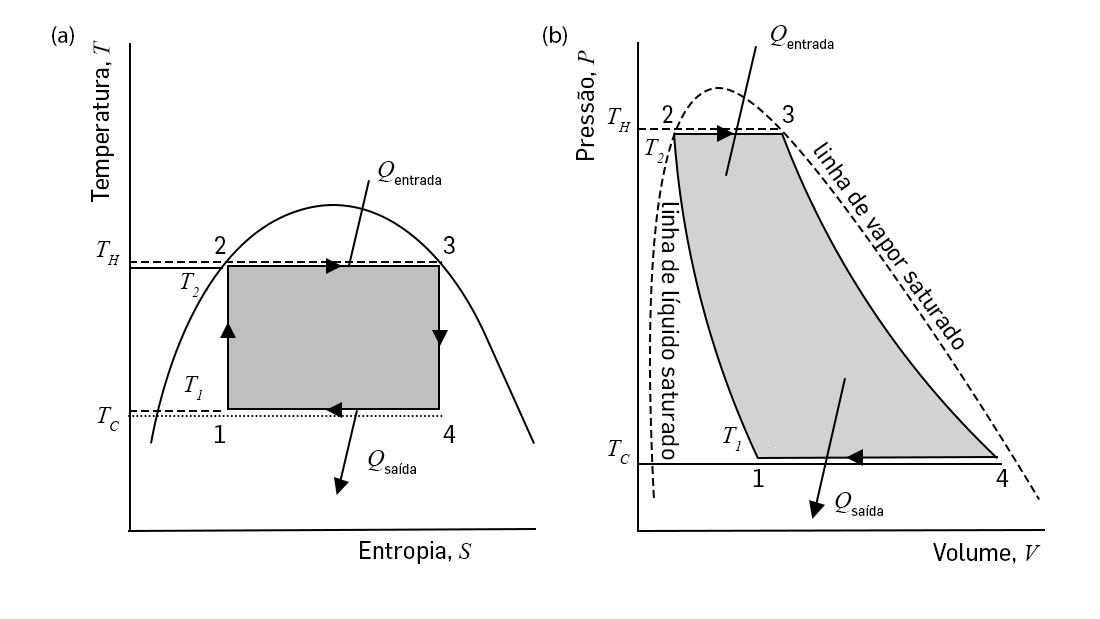
Na prática, os rendimentos de máquinas térmicas ou frigoríficas ficam abaixo dos máximos permitidos pela Termodinâmica. São inevitáveis fugas de calor nas transformações adiabáticas, atritos na realização do trabalho e trocas de calor com as paredes do recipiente. Além disto, o emprego de gases, com as suas baixas capacidades calorificas e alterações de volume limitadas pelo tamanho da máquina, tornam ainda mais ineficientes tais ciclos térmicos. São muito mais usados fluidos (e.g., água) para temperaturas de funcionamento abaixo dos seus pontos críticos (ver "Equilíbrio Vapor-Líquido próximo do ponto crítico") aproveitando-se, dessa forma, a transição líquido-vapor, pois que apresentam não só elevados calores latentes como também exibem grandes variações de volume nas duas fases (basta lembrar que 18g de água ocupam cerca de 18 cm3 na fase liquida e 22.400 cm3 na fase de vapor). Na FIGURA 5 é exibido um desses ciclos. Seja como for, o máximo rendimento obtido é \(1-\frac{T_{2}}{T_{1}}\) como exigido pelas leis da Termodinâmica.
Os ciclos termodinâmicos mantêm-se actuais, sendo utlizados na geração de energia eléctrica em centrais térmicas ou nucleares.
Referências
- PERMI, E. Thermodynamics, Important Books, ISBN-13: 978-8087830611. 2013.
- LAGE, E. Introdução à Termodinâmica, Rev. Ciência Elem., V7(2):020. (2019). DOI: 10.24927/rce2019.020.
- LAGE, E. Equilíbrio líquido-vapor próximo do ponto crítico, Rev. Ciência Elem., V7(3):061. (2019). DOI: 10.24927/ rce2019.061.
Recursos relacionados disponíveis na Casa das Ciências:
Criada em 30 de Agosto de 2019
Revista em 10 de Janeiro de 2020
Aceite pelo editor em 28 de Fevereiro de 2020

