Equação do 2º grau
Referência : Tavares, J., Geraldo, A., (2020) Equação do 2º grau, Rev. Ciência Elem., V8(1):003
Autores: João Nuno Tavares e Ângela Geraldo
Editor: José Ferreira Gomes
DOI: [http://doi.org/10.24927/rce2020.003]

Índice |
Resumo
Uma equação do 2º grau (ou equação quadrática) é qualquer equação da forma \(ax^2 + bx +c=0\) onde x representa a incógnita e a, b e c representa números conhecidos com \(a ≠ 0\).
Equações do 2ºgrau incompletas
Uma equação do 2º grau (ou equação quadrática) incompleta é uma equação do tipo \(ax^2+c=0\) ou \(ax^2+bx=0\), onde \(a,b\) e \(c\) são números reais ou complexos com \(a \neq 0\). Para resolver uma equação incompleta do tipo \(ax^2+c=0\) usamos as operações usuais de resolução de equações do 1ºgrau. Logo,
\(\displaystyle ax^2+c=0 \, \Longleftrightarrow \, ax^2=-c \, \Longleftrightarrow \, x^2=\frac{-c}{a} \, \Longleftrightarrow \, x=-\sqrt{\frac{-c}{a}} \, \vee \, x=\sqrt{\frac{-c}{a}}\)
- Se \(c=0\) a equação tem apenas uma solução em \(x=0\);
- Se \(c<0\) as soluções da equação são os números reais \(\displaystyle x=-\sqrt{\frac{|c|}{a}} \, \vee \, x=\sqrt{\frac{|c|}{a}}\);
- Finalmente se \(c>0\), a equação \(ax^2+c=0\), tem duas soluções complexas em \(\displaystyle x=-i\sqrt{\frac{|c|}{a}} \, \vee \, x=i\sqrt{\frac{|c|}{a}}\).
Já para resolver uma equação quadrática do tipo \(ax^2+bx=0\), comecemos por notar que \(ax^2+bx\) pode ser escrito como um produto de fatores (observemos que a incógnita \(x\) é comum aos dois termos e por isso podemos colocar \(x\) em evidência). Assim, usando o produto de fatores e a lei do anulamento do produto podemos resolver a equação da seguinte forma:
\(\displaystyle ax^2+bx=0 \, \Longleftrightarrow \, x(ax+b)=0 \, \Longleftrightarrow \, x=0 \, \vee \, ax+b=0 \, \Longleftrightarrow \, x=0 \, \vee \, x=\frac{-b}{a}\)
Equações do 2ºgrau completas
Uma equação do 2º grau completa é do tipo
\( a\,x^2+b\,x+c=0 \)
onde \(a,b\) e \(c\) são números reais ou complexos com \(a\neq 0\). Para resolver esta equação podemos "completar o quadrado", fazendo o seguinte
\(\begin{array}{lllllll} a\,x^2+b\,x+c &=& 0 & \Longleftrightarrow & x^2+\displaystyle\frac{b}{a} \,x+ \displaystyle\frac{c}{a}\,=\,0 & & \\ & & & \Longleftrightarrow & x^2+\displaystyle\frac{b}{a} \,x + \left(\displaystyle\frac{b}{2a}\right)^2- \left(\displaystyle\frac{b}{2a}\right)^2+ \displaystyle\frac{c}{a} &=&0 \\ & & & \Longleftrightarrow & \left(x+\displaystyle\frac{b}{2a}\right)^2- \left(\displaystyle\frac{b}{2a}\right)^2+ \displaystyle\frac{c}{a} \,=\,0 & & \\ & & & \Longleftrightarrow & \left(x+\displaystyle\frac{b}{2a}\right)^2 \,=\, \displaystyle\frac{b^2-4ac}{4a^2} & & \\ & & & \Longleftrightarrow & x+\displaystyle\frac{b}{2a} \,=\, \pm\displaystyle\frac{\sqrt{b^2-4ac}}{2a} & & \\ \end{array}\)
donde se deduz finalmente a famosa fórmula resolvente
\[x \,=\, \displaystyle\frac{-b\pm\sqrt{b^2-4ac}}{2a}\]
- Se o discriminante \(\Delta=b^2-4ac\) for igual a zero, a equação tem uma única raiz dupla igual a \(\displaystyle x=\frac{-b}{2a}\);
- Se \(\Delta>0\) a equação tem duas raízes reais distintas \(x_1\) e \(x_2\) tais que \(\displaystyle x_1=\frac{-b+\sqrt{\Delta}}{2a}\) e \(\displaystyle x_2=\frac{-b-\sqrt{\Delta}}{2a}\);
- Já se \(\Delta <0\) a equação não tem soluções reais mas tem duas raízes complexas \(x_1\) e \(x_2\) tais que \(\displaystyle x_1=\frac{-b+i\sqrt{|\Delta|}}{2a}\) e \(\displaystyle x_2=\frac{-b-i\sqrt{|\Delta|}}{2a}\).
| Mova os seletores a, b e c para alterar os coeficentes da função quadrática \(p(x)\).
As soluções da equação \(p(x)=0\) correspondem aos valores das abcissas de \(x_1\) e \(x_2\) (se existirem em \(\mathbb{R}\)). Observe que se \(x_1\) e \(x_2\) não existirem, os valores de \(z_1\) e \(z_2\) correspondem às raízes complexas da equação \(p(x)=0\). |
Resolução geométrica de al-Khwarizmi
Abu Abdullah Mohammed ben Musa Al-Khwarizmi (Khwarizm, Uzbequistão ? 780 – Bagdá ? 850) foi um matemático árabe, também astrónomo, geógrafo e historiador. É de seu nome que deriva o termo “algarismo”, em português. Foi um dos primeiros matemáticos a trabalhar na Casa da Sabedoria, em Baghdad, durante o reinado do califa al-Mamum (813-833).
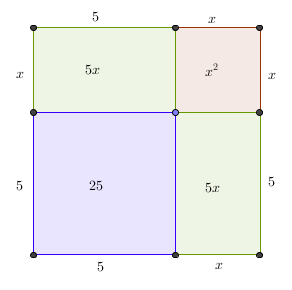
Para ilustrar a resolução de uma equação de 2º grau proposta por al-Khwarizmi, vamos utilizar a equação
\( x^2+10\,x=39 \)
A resolução é puramente geométrica. O quadrado \(x^2\) e o produto \(10\,x\) são representados literalmente por um quadrado de lado \(x\) e por dois rectângulos de lados 5 e \(x\), respectivamente, como se ilustra na figura 1.
O quadrado extra de área 25 "completa o quadrado" de lado \(5+x\), sendo a área total deste quadrado igual a 25+39 = 64, uma vez que \(x^2+10\,x=39\). Portanto
\(\mbox{área do quadrado grande} = (x+5)^2=64 \ \ \Longrightarrow \ \ x+5=8 \ \ \Longrightarrow \ \ x=3 \)
al-Khwarizmi não admitia comprimentos negativos e, por isso, não considera a solução \(x=-13\) da equação \(x^2+10\,x=39\).
Um problema muito antigo
Os problemas que conduzem à resolução de uma equação do segundo grau estão entre os mais antigos da Matemática. Em textos cuneiformes escritos pelos babilónicos há 4 mil anos atrás, encontrámos, por exemplo, o problema de encontrar dois números conhecendo a sua soma \(s\) e o seu produto \(p\).
Em termos geométricos, se os dois números \(s\) e \(p\) forem estritamente positivos, este problema consiste em determinar os comprimentos dos lados de um retângulo, conhecendo o semi-perímetro \(s\) e a sua área \(p\).
Os números procurados são as raízes da equação de 2º grau \(x^2-sx+p=0\).
De facto, se um dos números é \(x\), o outro número será \(s-x\), o seu produto é \(p=x(s-x)=sx-x^2\) e portanto \(x^2-sx+p=0\).
Exemplo
Consideremos então o problema de encontrar dois números cuja soma é igual a \(8\), ou seja \(s=8\), e cujo produto é igual a \(-65\), ou seja \(p=-65\). Os números procurados serão então as soluções da equação quadrática \(x^2-8x-65=0\). Pela fórmula resolvente temos então que:
\(\displaystyle x=\frac{-(-8) \pm \sqrt{8^2-4 \times 1 \times (-65)}}{2 \times 1} \, \Longleftrightarrow \, x=\frac{8 \pm \sqrt{324}}{2} \, \Longleftrightarrow \, x=\frac{8+18}{2} \, \vee \, x=\frac{8-18}{2} \, \Longleftrightarrow \, x=13 \, \vee \, x=-5\).
Os números procurados são então o número \(13\) e o número \(-5\). Podemos verificar que \(s=13+(-5)=8\) e que \(p=13 \times (-5)=-65\).
Criada em 24 de Novembro de 2012
Revista em 7 de Janeiro de 2020
Aceite pelo editor em 28 de Fevereiro de 2020