Diferenças entre edições de "Referenciais"
| Linha 21: | Linha 21: | ||
| | ||
|| | || | ||
| + | | ||
A cada ponto \(A\) do plano associamos, de forma unívoca, o par de <span style="color:blue">'''coordenadas'''</span> relativas a esse sistema de eixos (ou referencial). | A cada ponto \(A\) do plano associamos, de forma unívoca, o par de <span style="color:blue">'''coordenadas'''</span> relativas a esse sistema de eixos (ou referencial). | ||
Revisão das 22h34min de 14 de janeiro de 2013
Referência : Não citável Esta página ainda não foi aprovada.
Autor: João Nuno Tavares e Ângela Geraldo
Editor: Colocar nome do editor
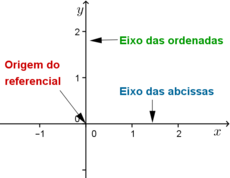
Referencial Cartesiano no plano
Um referencial cartesiano no plano é um sistema constituído por dois eixos ortogonais (ou seja, dois eixos perpendiculares) - o eixo das abcissas ou eixo dos \(xx\) e o eixo das ordenadas ou eixo dos \(yy\). Ao ponto de intersecção dos dois eixos chamamos de origem.
Um referencial cartesiano no plano serve para estudar geometria plana com ajuda de álgebra, isto é, estudar Geometria Analítica em duas dimensões (2D).
|
A cada ponto \(A\) do plano associamos, de forma unívoca, o par de coordenadas relativas a esse sistema de eixos (ou referencial). \[A \quad \longleftrightarrow \quad (x_A,y_A) \in \mathbb{R}^2\] \(x_A\) diz-se a abcissa e \(y_A\) a ordenada do ponto \(A\). Escrevemos então:
|
Referencial Cartesiano no espaço
Um referencial cartesiano no espaço é um sistema constituído por três eixos ortogonais (ou seja, três eixos perpendiculares entre si) - o eixo das abcissas, o eixo das ordenadas e o eixo das cotas ou eixo dos \(zz\).