Diferenças entre edições de "Equação do 2º grau"
(→Resolução geométrica de al-Khwarizmi) |
|||
| Linha 20: | Linha 20: | ||
O quadrado extra de área 25 "completa o quadrado" de lado \(5+x\), sendo a área total deste quadrado igual | O quadrado extra de área 25 "completa o quadrado" de lado \(5+x\), sendo a área total deste quadrado igual | ||
| − | a 25+39=64, uma vez que \(x^2+10\,x=39\). Portanto | + | a 25+39 = 64, uma vez que \(x^2+10\,x=39\). Portanto |
<div style="text-align: center;"> | <div style="text-align: center;"> | ||
| Linha 26: | Linha 26: | ||
</div> | </div> | ||
| + | al-Khwarizmi não admitia comprimentos negativos e, por isso, não considera a solução x=-13$ da equação \(x^2+10\,x=39\). | ||
| + | |||
| + | =Resolução de Descartes= | ||
Revisão das 22h27min de 24 de novembro de 2012
Referência : Não citável Esta página ainda não foi aprovada.
Autor: João Nuno Tavares e Ângela Geraldo
Editor: Colocar nome do editor
Definição e resolução
Resolução geométrica de al-Khwarizmi
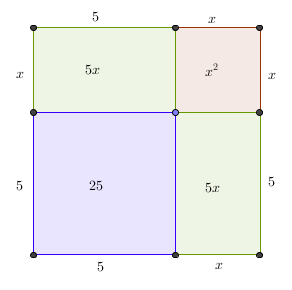
Para ilustrar a resolução de uma equação de 2º grau proposta poral-Khwarizmi, vamos utilizar a equação
\(x^2+10\,x=39\)
A resolução é puramente geométrica. O quadrado \(x^2\) e o produto \(10\,x\) são representados literalmente por um quadrado de lado \(x\) e por dois rectângulos de lados 5 e \(x\), respectivamente, como se ilustra na figura 1.
O quadrado extra de área 25 "completa o quadrado" de lado \(5+x\), sendo a área total deste quadrado igual a 25+39 = 64, uma vez que \(x^2+10\,x=39\). Portanto
\(\mbox{área do quadrado grande} = (x+5)^2=64 \ \ \Longrightarrow \ \ x+5=8 \ \ \Longrightarrow \ \ x=3 \)
al-Khwarizmi não admitia comprimentos negativos e, por isso, não considera a solução x=-13$ da equação \(x^2+10\,x=39\).
Resolução de Descartes
em construção