Referenciais uniformes equiangulares

Referência : Sá, N., (2021) Referenciais uniformes equiangulares, Rev. Ciência Elem., V9(2):047
Autor: Nuno Sá
Editor: José Ferreira Gomes
DOI: [https://doi.org/10.24927/rce2021.047]

---

Resumo

Um conjunto de linhas diz-se equiangular se os ângulos internos entre qualquer par de linhas for o mesmo. E diz-se uniforme se se espalhar pelo espaço da maneira mais uniforme possível (num sentido descrito mais precisamente no texto). Os versores dum conjunto de linhas uniforme e equiangular constituem uma base para um referencial uniforme equiangular, sendo os referenciais cartesianos um caso particular deste tipo de referencial que ocorre em todas as dimensões, mas podendo haver outros, o que depende crucialmente da dimensão do espaço. O problema de classificar todos os referenciais uniformes equiangulares para dimensões arbitrárias é um problema em aberto na Matemática.

Referenciais uniformes

Um referencial uniforme normalizado para um espaço vetorial \(d\)-dimensional é um conjunto de \(n\geq d\) vetores unitários \(\vec{u}_{i}\) para o qual qualquer vetor desse espaço admite a decomposição

\(\vec{v}=\frac{d}{n}\sum_{i=1}^{n}c_{i}\vec{u}_{i}\vec{u}_{i}\) sendo \(c_{i}=\vec{u}_{i}\cdot \vec{v}\) (1)

Quando \(n = d\) o referencial uniforme é uma base ortonormada. Quando \(n > d\) a redundância da informação contida num maior número de componentes \(c_{i}\) do que a dimensão do espaço encontra aplicações teóricas na Teoria da Informação e práticas nas Telecomunicações.

Um referencial uniforme pode ser representado na forma duma matriz \(u\) cujas componentes \(\mu_{ki}\) são a \(k\)-ésima coordenada do vetor \(\vec{u}_{i}\)

\(u=\begin{bmatrix} \mu_{11} & \mu_{12} & ... & \mu_{1n}\\ ... & ... & ... & ...\\ \mu_{d1} & \mu_{d2} & ... & \mu_{dn} \end{bmatrix}\) (2)

Pode-se mostrar que a condição (1) é equivalente a

\(u\cdot u^{T}=\frac{n}{d}I_{d}\). (3)

Retas equiangulares

Um conjunto de retas equiangulares pode ser descrito por \(n\) vetores unitários \(\vec{u}_{i}\) para os quais o produto interno entre qualquer par deles seja o mesmo:

\(\left ( u\cdot u^{T} \right )_{ij}=\vec{\mu}_{i}\cdot\vec{\mu}_{j}=\left\{\begin{matrix} 1 & \textrm{se} & i=j\\ \pm p & \textrm{se} & i\neq j \end{matrix}\right.\) (4)

Os dois sinais possíveis para o produto interno refletem a arbitrariedade na escolha do sentido do vetor que representa cada reta. O ângulo comum feito entre todos os pares de retas é \(\theta=\textrm{cos}^{-1}p\).

A existência de retas equiangulares é um problema antigo, dependente da dimensão \(d\) do espaço e do número \(n\) de retas. Pode não ter solução ou ter uma ou mais soluções, cada uma para um diferente valor do “ângulo” \(p\), mas tem que ser \(n\leq d\left ( d+1 \right )/2\). Este valor máximo de \(n\) só é possível para certas dimensões. Alguns conjuntos concretos de linhas equiangulares em diversas dimensões podem ser encontrados em.

Quando os vetores dum referencial uniforme representam retas equiangulares, eles podem então ser descritos por matrizes retangulares \(n \times d\) que obedeçam às equações (3) e (4) para \(u\cdot u^{T}\) e para \(u^{T} \cdot u\). Pode-se mostrar^, que, quando a solução existe, o ângulo \(p\) entre as linhas é dado por

\(p^{2}=\frac{n-d}{d\left ( n-1 \right )}\) (5)

e que tem que ser

\(d\leq n\leq \frac{d\left ( d+1 \right )}{2}\) (6)

Exemplos

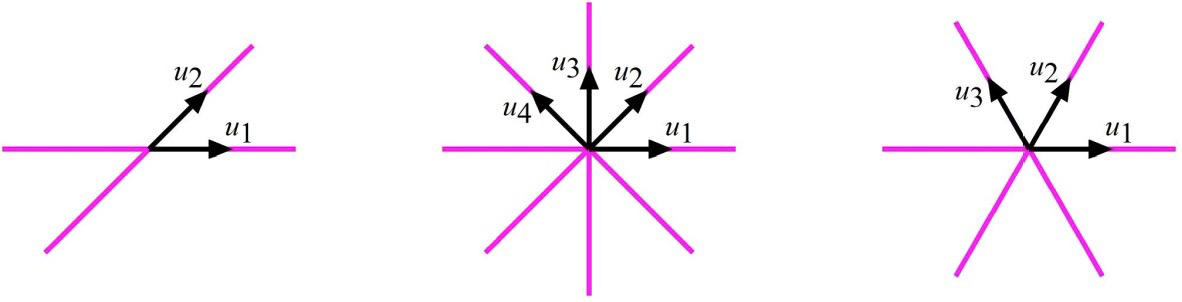
Na FIGURA 1 apresentamos três casos para ilustrar o conceito de referencial uniforme equiangular. Temos:

Esquerda \(u=\begin{bmatrix} 1 & \frac{1}{\sqrt{2}}\\ 0 & \frac{1}{\sqrt{2}} \end{bmatrix}\), \(u\cdot u^{T}=\begin{bmatrix} \frac{3}{2} & \frac{1}{2}\\ \frac{1}{2} & \frac{1}{2} \end{bmatrix}\) e \(u^{T}\cdot u=\begin{bmatrix} 1 & \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} & 1 \end{bmatrix}\)

Meio \(u=\begin{bmatrix} 1 & \frac{1}{\sqrt{2}} & 0 & -\frac{1}{\sqrt{2}}\\ 0 & \frac{1}{\sqrt{v}} & 1 & \frac{1}{\sqrt{2}} \end{bmatrix}\), \(u\cdot u^{T}=\begin{bmatrix} 2 & 0\\ 0 & 2 \end{bmatrix}\) e \(u^{T}\cdot u=\begin{bmatrix} 1 & \frac{1}{\sqrt{2}} & 0 & -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} & 1 & \frac{1}{\sqrt{2}} & 0\\ 0 & \frac{1}{\sqrt{2}} & 1 & \frac{1}{\sqrt{2}}\\ -\frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} & 1 \end{bmatrix}\);

Direita \(u=\begin{bmatrix} 1 & \frac{1}{2} & \frac{1}{2}\\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix}\), \(u\cdot u^{T}=\begin{bmatrix} \frac{3}{2} & 0\\ 0 & \frac{3}{2} \end{bmatrix}\) e \(u^{T}\cdot u=\begin{bmatrix} 1 & \frac{1}{2} & \frac{1}{2}\\ \frac{1}{2} & 1 & -\frac{1}{2}\\ \frac{1}{2} & -\frac{1}{2} & 1 \end{bmatrix}\).

FIGURA 1. O sistema de eixos da esquerda é equiangular, pois só tem duas retas, mas não é uniforme - falha a equação (3). O do meio é uniforme mas não é equiangular, pois cada reta faz ângulos de 45° ou de 90° com as outras - falha a equação (4). O da direita é um referencial uniforme equiangular.

Soluções

Não dispomos de um método sistemático para encontrar referenciais uniformes equiangulares para todas as dimensões. Sabemos que existem as seguintes soluções triviais:

• Para \(d = 1\) qualquer valor de \(n\) fornece uma solução com \(p = 1\).
• Quando \(n = d\) os referenciais ortonormados são soluções com \(p = 0\).
• Quando \(n = d + 1\) há sempre solução com \(p = 1/d\).

Fora destes casos, sabemos que, para que haja solução (mas sem a garantir), é necessário que se verifiquem as seguintes condições:

• Se \(n = 2d\)

\(n=a^{2}+b^{2}+1\) com \(a,b\in \mathbb{N}\) (7)

• Caso contrário

\(\sqrt{\frac{d\left ( n-1 \right )}{n-d}}\) e \(\sqrt{\frac{\left ( n-d \right )\left ( n-1 \right )}{d}}\) são inteiros ímpares. (8)

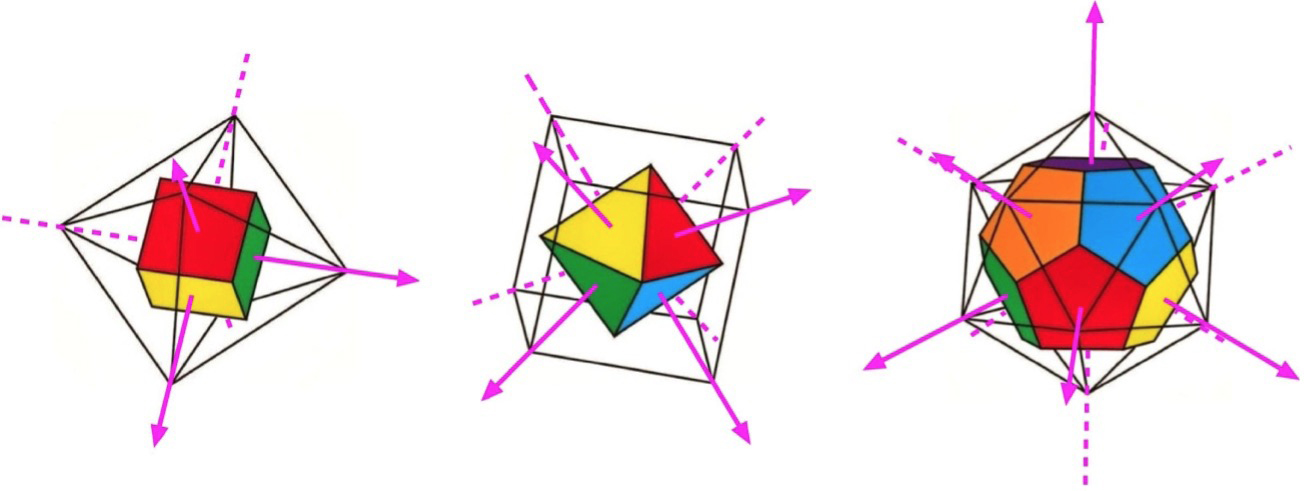
Para as dimensões mais baixas conhecem-se todas as soluções. Em duas dimensões só há as duas soluções triviais: os dois eixos cartesianos e os três eixos do exemplo da direita na FIGURA 1. Em três dimensões há as três soluções representadas na FIGURA 2, uma delas não sendo trivial. Na TABELA 1 indicamos os valores de \(n\) e de \(p\) para as soluções não triviais existentes até à dimensão \(d = 11\). Tabelas mais extensas podem ser encontradas em4.

FIGURA 2. Em 3 dimensões há três soluções: \(n = d = 3\) eixos ortogonais fazendo ângulos de 90° (trivial), \(n = d+1 = 4\) eixos fazendo ângulos de \(\textrm{cos}^{-1}\left ( 1/3 \right )=70,53\)° (trivial) e \(n = 2d = 6\) eixos fazendo ângulos de \(\textrm{cos}^{-1}\left ( 1/\sqrt{5} \right )=63,43\). Todas elas são facilmente visualizáveis usando os eixos que unem as faces opostas ou os vértices opostos de sólidos platónicos. No primeiro caso as 6 faces dum cubo ou os 6 vértices dum octaedro, no segundo caso as 8 faces dum octaedro ou os 8 vértices dum cubo e no terceiro caso as 12 faces dum dodecaedro ou os 12 vértices dum icosaedro.

TABELA 1. O problema dos referenciais uniformes equiangulares é muito irregular na dimensão: para certas dimensões não há soluções não triviais e para outras há mais do que uma.

Espaços complexos

A definição de referencial uniforme equiangular, equações (3) e (4), mantém-se para espaços vetoriais complexos, apenas com a seguinte modificação em (4):

\(\left | \vec{\mu}_{i}\cdot \vec{\mu}_{j} \right |=p\) se \(i\neq j\) (9)

As equações (2) e (5) mantêm-se válidas no caso complexo, mas não (6), que passa a ser:

\(d\leq n\leq d^{2}\). (10)

Os referenciais uniformes equiangulares máximos, isto é, para os quais \(n=d^{2}\), desempenham um importante papel na Teoria da Informação Quântica, visto que os espaços vetoriais da Mecânica Quântica são complexos, com possíveis aplicações no domínio da computação quântica.

Referências

---

Criada em 23 de Fevereiro de 2021
Revista em 19 de Março de 2021
Aceite pelo editor em 15 de Junho de 2021