Série de Lyman
Referência : Lima, L.S., (2015) Série de Lyman, Rev. Ciência Elem., V3(3):193
Autores: Luis Spencer Lima
Editor: Jorge Gonçalves
DOI: [http://doi.org/10.24927/rce2015.193]
A série de Lyman corresponde ao conjunto de transições electrónicas num átomo de hidrogénio responsáveis pela emissão de radiação na zona do ultra-violeta (UV). As transições electrónicas que caracterizam esta série dão-se de um estado excitado (n 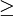 2) para o nível n = 1.
2) para o nível n = 1.
Esta série foi assim designada em homenagem ao seu descobridor Theodore Lyman, um físico norte-americano. Lyman descobriu as restantes linhas espectrais no período entre 1906 e 1914.
Todas as transições estão situadas na região UV, dado o comprimento de onda da radiação emitida ser inferior a 400 nm. Cada transição é designada de forma sequencial por uma letra do alfabeto grego. Assim, a primeira transição (n = 2 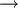 n = 1) é designada por Lyman-alfa (Ly-
n = 1) é designada por Lyman-alfa (Ly-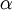 ), a segunda transição (n = 3
), a segunda transição (n = 3 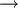 n = 1) denomina-se Lyman-beta (Ly-
n = 1) denomina-se Lyman-beta (Ly-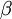 ) e assim sucessivamente. As características das transições da série de Lyman estão compiladas na tabela seguinte:
) e assim sucessivamente. As características das transições da série de Lyman estão compiladas na tabela seguinte:
| Transição | 2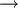 1 1 |
3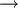 1 1 |
4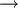 1 1 |
5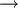 1 1 |
6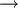 1 1 |
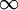 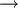 1 1 |
|---|---|---|---|---|---|---|
| Nome | Ly-
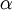 |
Ly- 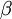 |
Ly- 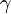 |
Ly- 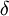 |
Ly- 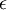 |
|
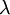 /nm[1] /nm[1] |
121,6 |
102,5 |
97,2 |
94,9 |
93,7 |
91,15 |
Energia / kJ mol-1 mol-1 |
983,8 |
1167 |
1231 |
1261 |
1277 |
1312 |
A previsão do comprimento de onda da radiação emitida pelas transições electrónicas da série de Lyman e consequente valor energético, pode ser efectuada através da fórmula de Rydberg. Esta fórmula foi desenvolvida pelo físico sueco Johannes Rydberg entre 1888 e 1890 tendo como base a fórmula empírica desenvolvida pelo matemático suíço Johann Balmer (fórmula de Balmer). A equação de Rydberg, a seguir apresentada, permite o cálculo do comprimento de onda de qualquer transição electrónica para o átomo de hidrogénio:
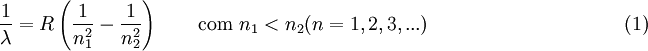
Nesta equação, n1 e n2 representam os níveis atómicos correspondentes à transição electrónica n2 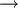 n1 e R representa a constante de Rydberg, R = 1,097 373 156 852 5 (73)
n1 e R representa a constante de Rydberg, R = 1,097 373 156 852 5 (73)  107 m-1. No caso da série de Lyman, n1 = 1.
107 m-1. No caso da série de Lyman, n1 = 1.
Referências
1. http://en.wikipedia.org/wiki/Lyman_series, consultada em 22/01/2010
Criada em 7 de Março de 2010
Revista em 6 de Setembro de 2010
Aceite pelo editor em 31 de Outubro de 2015

