Ondas eletromagnéticas
Referência : Lage, E., (2024) Ondas eletromagnéticas, Rev. Ciência Elem., V12(1):002
Autores: Eduardo Lage
Editor: João Nuno Tavares
DOI: [https://doi.org/10.24927/rce2024.002]

Resumo
As equações fundamentais do Eletromagnetismo admitem soluções que se propagam nos meios como ondas do campo eletromagnético. Dielétricos ou condutores definem a relação de dispersão, a relação entre a frequência e o vetor de onda. Esta relação, obtida através dos modelos simples de Lorentz e Drude, é complexa nos metais e também nos dielétricos para frequências próximas de ressonâncias, em ambos os casos levando ao decaímento da amplitude da onda no tempo ou no espaço. A caracterização do campo transportado pela onda faz intervir o conceito de polarização e a velocidade a que se propaga define o índice de refração do meio, verificando-se que são reproduzidas as leis da óptica geométrica, mas indo para além delas como é bem exibido pela reflexão total frustrada, um fenómeno característico da natureza ondulatória da radiação.
Uma onda eletromagnética é uma perturbação do campo eletromagnético que se propaga através do meio onde é gerada. Nesse meio, os campos elétrico e magnético variam no tempo e no espaço originando, dessa forma, um transporte de energia e momento[1]. No caso mais simples, a dependência temporal é sinusoidal, com uma frequência angular \(\omega\), dizendo-se então que a onda é monocromática. Em meios homogéneos, a caracterização mais simples para o campo faz intervir o conceito de onda[2] plana, uma condição periódica no espaço definida pelo vetor de onda \(\vec{k}\). A natureza do meio determina a relação entre \(\omega\) e \(\vec{k}\), designada por relação de dispersão. Embora seja comum tratar-se separadamente a propagação da onda em meios puramente dielétricos ou puramente condutores, há vantagem em considera-los em conjunto não só porque qualquer meio material apresenta simultaneamente aqueles limites como o formalismo é essencialmente o mesmo. Em qualquer caso, o meio será considerado isotrópico e linear, i.e., admitem-se relações lineares entre o deslocamento elétrico, \(\vec{D}\), e o campo elétrico, \(\vec{E}\), bem como entre o campo magnético, \(\vec{B}\), e a sua intensidade, \(\vec{H}\).
Em tais meios, as equações de Maxwell escrevem-se[3]:
\(\bigtriangledown \cdot \vec{D}=\rho^{\left ( l \right )}\) (1)
\(\bigtriangledown \cdot \vec{B}=0\) (2)
\(\bigtriangledown \wedge \vec{E}=-\frac{\partial \vec{B}}{\partial t}\) (3)
\(\bigtriangledown \wedge \vec{H}=\vec{i}^{\left ( l \right )}+\frac{\partial \vec{D}}{\partial t}\) (4)
onde \(\rho^{\left ( l \right )}\) e \(\vec{i}^{\left ( l \right )}\) são, respetivamente, as densidades de carga e corrente livres satisfazendo à lei de conservação:
\(\frac{\partial \rho^{\left ( l \right )}}{\partial t}+\bigtriangledown \cdot \vec{i}^{\left ( l \right )}=0\) (5)
Estas cargas e correntes são importantes em meios condutores onde será admitida a lei de Ohm:
\(\vec{i}^{\left ( l \right )}=\sigma \vec{E}\) (6)
Aqui, para simplificar, admite-se que o meio é não magnético:
\(\vec{B}=\mu_0\vec{H}\) (7)
Com a relação linear entre \(\vec{D}\) e \(\vec{E}\), que se especificará a seguir, todas as equações anteriores são lineares pelo que a solução geral é a sobreposição de ondas planas e monocromáticas.
Para qualquer destas ondas, os campos variam no espaço e no tempo sob a forma e \(e^{i\vec{k}\cdot\vec{r}-i\omega t}\).
Nestas condições, a relação referida fica:
\(\vec{D}=\varepsilon \vec{E}\) (8)
É importante notar que a permitividade elétrica, \(\omega\), depende, em geral de \(\omega\) e \(\vec{k}\). O modelo de Lorentz, tratado no Apêndice de Polarização elétrica e magnetização, fornece uma expressão simples, reproduzindo-se, a seguir, o resultado aí obtido para um oscilador harmónico (frequência natural \(\omega_0\) e constante de amortecimento \(\gamma \)):
\(\chi _e\left ( \omega \right )=\frac{nq^2}{m\varepsilon _0}\frac{1}{\omega_{0}^{2}-\omega^2-i\gamma\omega}\rightarrow \frac{\varepsilon }{\varepsilon _0}\equiv \varepsilon _r\left ( \omega \right )=1+\chi _e\left ( \omega \right )\) (9)
onde \(n\) é a densidade de tais osciladores. No caso geral, a suscetibilidade apresenta-se como uma soma sobre os diferentes modos de vibração de moléculas ou da rede cristalina do dielétrico, cada um com a sua frequência própria característica. Note-se, porém, que nem todos os modos contribuem: no exemplo da FIGURA 6A) em Vibrações, se os dois osciladores tiverem cargas iguais e opostas, apenas o modo anti-simétrico responde a uma onda cujo comprimento seja muito maior que a distância entre os osciladores. A FIGURA 1 exibe as partes real e imaginária da suscetibilidade representada na equação (9).
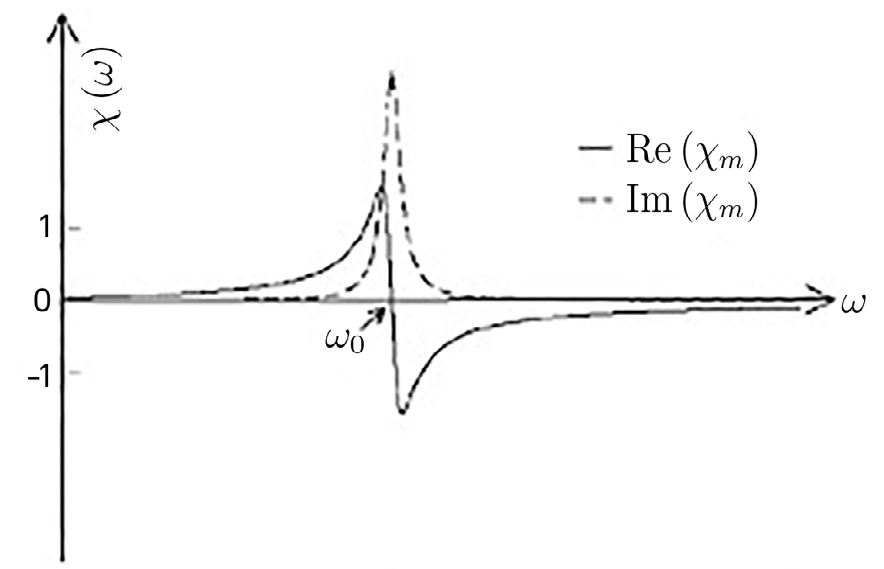
Notar-se-á que a parte real da suscetibilidade cresce com a frequência até perto da ressonância em \(\omega_0\) onde decresce abrutamente, sendo também aí que se concentra a parte imaginária a qual determina absorção ressonante de energia. Para uma colecção de tais osciladores (molécula, sólido), a suscetibilidade apresenta-se como uma sobreposição de ressonâncias para diferentes frequências próprias.
Note-se que para frequências muito maiores que a frequência própria de oscilação, a suscetibilidade decai rapidamente, obtendo-se, da equação (9):
\(\varepsilon _r\left ( \omega \right )\approx 1-\frac{nq^2}{m\varepsilon _0\omega^2}\) (10)
Em metais e outros condutores, o comportamento da onda eletromagnética é dominado pela condutividade, \(\sigma \), do material. No Apêndice é apresentado o modelo de Drude que fornece uma expressão simples para esta grandeza:
\(\sigma =n\frac{q_{e}^{2}}{m}\tau \) (11)
onde \(n\) é a densidade eletrónica e \(\tau\) é o tempo médio entre duas colisões sucessivas de um eletrão (com impurezas ou vibrações da rede cristalina). A condutividade varia com a frequência (e, sobretudo, com a temperatura), mas situa-se perto de \(10^7\Omega ^{-1}m^{-1}\) nos metais. A FIGURA 2 exibe esta dependência para três metais. Para condutores, a dissipação dá-se, evidentemente, por efeito Joule.
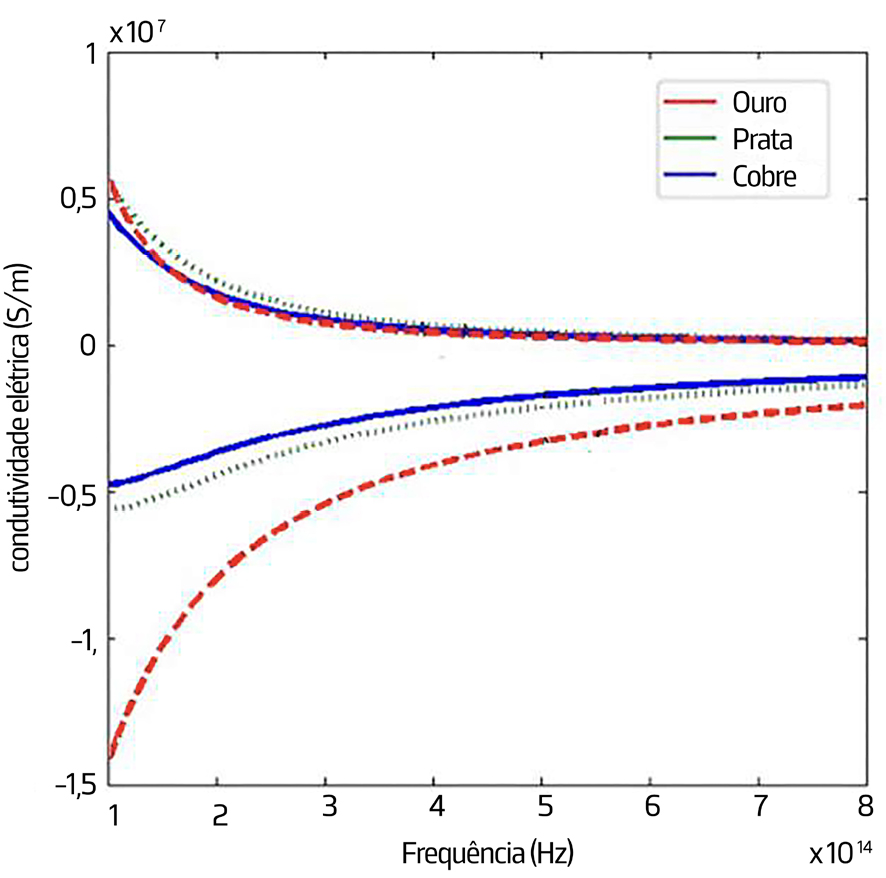
Para a onda plana monocromática, a equação (1) fica:
\(\vec{k}\cdot\vec{D}=\varepsilon \vec{k}\cdot\vec{E}=-i\rho^{\left ( l \right )}\)
Ora, a equação (5) dá:
\(\omega\rho^{\left ( l \right )}=\vec{k}\cdot\vec{i}^{\left ( l \right )}=\sigma \vec{k}\cdot\vec{E}\)
Substituindo na anterior, encontra-se:
\(\left ( \varepsilon +i\frac{\sigma }{\omega} \right )\vec{k}\cdot\vec{E}=0\rightarrow \vec{k}\cdot\vec{E}=0\) (12)
Deste modo, também é \(\rho^{\left ( l \right )}=0\): cargas livres só poderão surgir na superfície dos materiais.
Por outro lado, as equações (2) e (7) dão:
\(\vec{k}\cdot\vec{H}=0\) (13)
Estes dois importantes resultados mostram que as ondas eletromagnéticas, nos meios aqui considerados, são transversais para os campos elétrico e magnético (FIGURA 3).
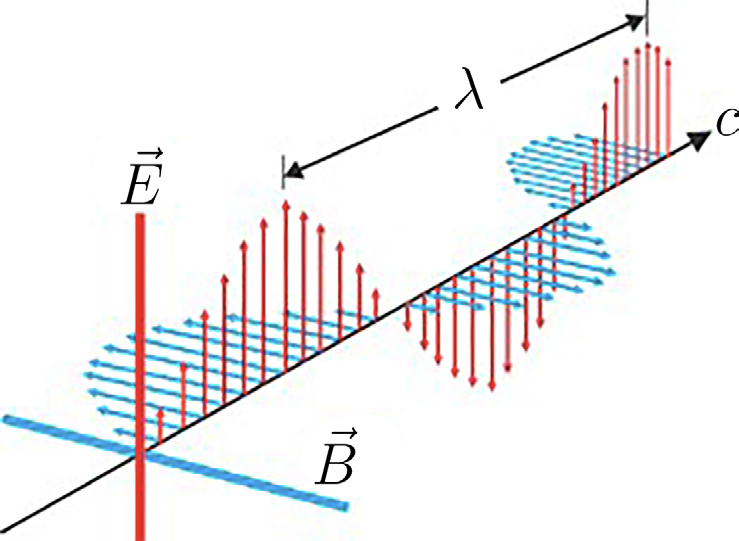
A equação (3) fica:
\(\vec{k}\wedge \vec{E}=\mu_0\omega\vec{H}\) (14)
e a equação (4) dá:
\(\vec{k}\wedge \vec{H}=\left ( \omega\varepsilon -i\sigma \right )\vec{E}\) (15)
Estes resultados indicam que o triedro \(\left ( \vec{E},\vec{H},\vec{k} \right )\) é direto, obtendo-se, também, a relação de dispersão:
\(k^2=\mu_0\left ( \varepsilon \omega^2-i\omega\sigma \right )\) (16)
No caso particular do vazio \(\left ( \sigma=0,\varepsilon =\varepsilon _0 \right )\), tem-se:
\(\omega^2=\frac{k^2}{\varepsilon _0\mu_0}\) (17)
Esta relação mostra que, no vazio, todas as ondas se propagam com a mesma velocidade de fase, \(v_f=\frac{1}{\sqrt{\varepsilon _0\mu_0}}\), caso em que se diz que não há dispersão. Esta velocidade foi deduzida por Maxwell[4] (1864) que, usando os valores da permitividade e permeabilidade conhecidos para o ar, obteve um valor muito próximo da velocidade da luz no vazio, \(c\). A identificação passou a ser universalmente aceite e a relação:
\(\varepsilon _0\mu_0c^2=1\) (18)
veio a adquirir um estatuto diferente. Com efeito, dada a importância da velocidade da luz na teoria da relatividade, optou-se modernamente por postular o seu valor:
\(c\) = 299792458m/s (19)
Tal permite definir a unidade de comprimento (o metro) porque a unidade de tempo (o segundo) é definida com extrema precisão usando relógios atómicos.
Assim, com o valor também postulado no S.I. \(\mu_0=4\pi\times 10^{-7}\)H/m, a equação (18) passou a definir a permitividade elétrica do vazio, \(\varepsilon _0\).
A relação de dispersão para o vazio, equação (17) aplica-se a todo o espectro eletromagnético exibido na FIGURA 4 onde se caracterizam diferentes regiões, em particular a do espectro visível.
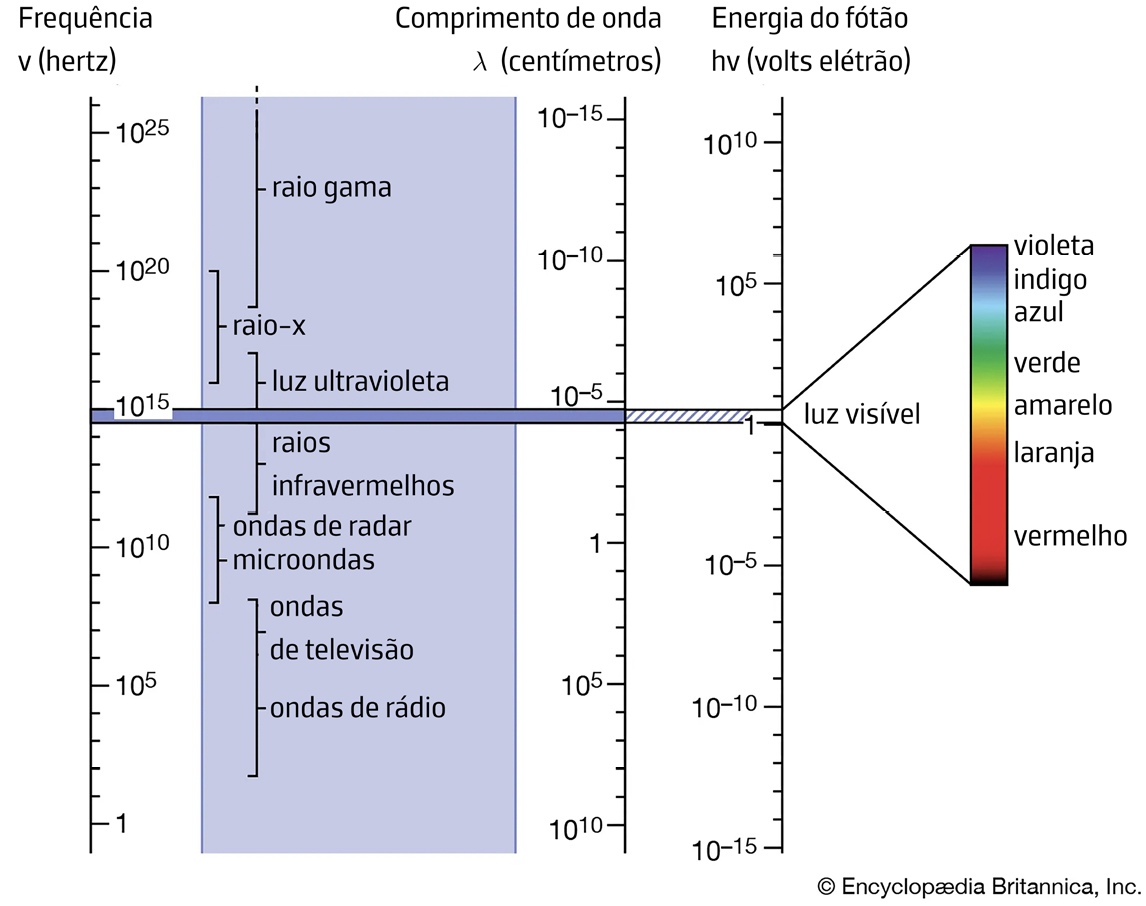
Regressando à equação (16), que significado tem uma relação de dispersão complexa? Ela não depende da direção do vetor de onda, como resulta da isotropia do meio. Considere-se, então, que essa direção é a do eixo \(z\), de modo que os campos variam como \(e^{ikz-i\omega t}\). Ora, duas situações ocorrem habitualmente:
1.ª A frequência é imposta por um emissor de radiação (por exemplo, antena). Assim, com \(\omega\) real, a equação (16) dá, em geral, um vetor de onda complexo, \(k=k'+ik''\) situado no primeiro quadrante, i.e., \(k''>0\) (e, claro, também a solução simétrica situada no terceiro quadrante). Se o emissor se situar em \(z = 0\), obtém-se \(e^{ikz-i\omega t}=e^{ik'z-i\omega t}e^{-k''z}\), i.e., a onda propaga-se com a velocidade de fase \(\frac{\omega}{k'}\) mas vai amortecendo a sua amplitude.
2.ª É imposto o vetor de onda, i.e., k real, como acontece, por exemplo, quando a onda oscila entre dois refletores (por exemplo, espelhos) no espaço entre os quais só é permitido um número inteiro de comprimentos de onda[5]. Nestas condições, a equação (16) dá a solução complexa \(\omega=\omega'-i\omega''\) situada no quarto quadrante (ou a sua simétrica, no segundo quadrante). Deste modo, os campos variam como \(e^{ikz-i\omega 't}e^{-\omega''t}\) representando uma propagação com decaímento no tempo. Este efeito não pode ser ignorado nos condutores e nos dielétricos quando a frequência está próxima da ressonância.
Nos dielétricos (isoladores), longe de ressonâncias, pode ignorar-se a parte imaginária da suscetibilidade, obtendo-se assim:
\(k^2=\omega_0\varepsilon \omega^2=\varepsilon _r\left ( \omega \right )\frac{\omega^2}{c^2}\) (20)
o que define a velocidade de fase e o índice de refração, \(\eta\), do material:
\(v_f\left ( \omega \right )=\frac{\omega}{k}=\frac{c}{\sqrt{\varepsilon _r\left ( \omega \right )}}\; \; \; \; \; \eta\equiv \frac{c}{v_f}=\sqrt{\varepsilon _r\left ( \omega \right )}\) (21)
À medida que \(\omega\) se aproxima de uma ressonância, \(\varepsilon _r\left ( \omega \right )\) cresce com \(\omega\) (ver FIGURA 1), originando o crescimento do índice de refração — é a dispersão normal, como acontece com luz num prisma de vidro (FIGURA 5) ou numa gota de água (é esta dispersão que origina o arco-íris).
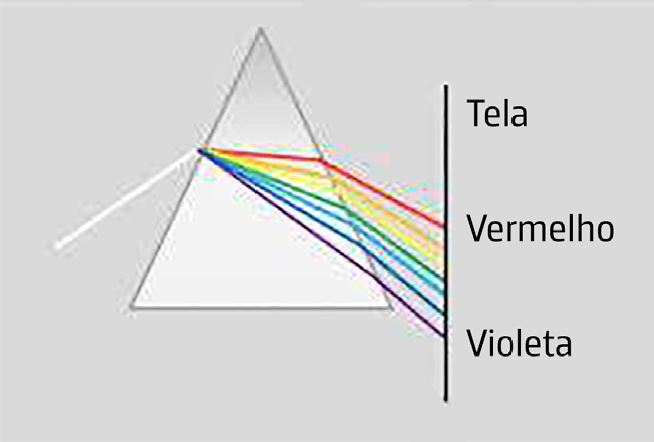
Mas próximo da ressonância, a parte real de \(\varepsilon _r\left ( \omega \right )\) decresce rapidamente, determinando uma diminuição do índice de refração com a frequência — é a dispersão anómala. Nessa mesma zona de frequências, não pode ser ignorada a parte imaginária de \(\varepsilon _r\left ( \omega \right )\), originando absorção por ressonância. Note-se que para frequências muito maiores que as frequências de ressonância dos dielétricos, a suscetibilidade é praticamente nula, pelo que \(\varepsilon _r\cong 1\) — o material é transparente para raios \(X\) ou \(\gamma\). Contudo, nestes regimes, o modelo baseado num oscilador harmónico não mais se aplica, devendo ser substituído por modelos atómicos nos quais a absorção existe para transições entre níveis energéticos de átomos ou moléculas, originando riscas espectrais de absorção, ou destes níveis para a parte contínua do espectro atómico, criando bandas contínuas. Também nos sólidos existem absorções por excitação eletrónica da banda de valência para a banda de condução ou, nos semicondutores, de estados atómicos de impurezas para aquelas bandas. Estes importantes tópicos não serão aqui considerados.
Estados de polarização da onda.
Alinhando o eixo \(z\) com o vetor de onda, os campos elétrico e magnético, em cada ponto do espaço, situam-se no plano perpendicular, sendo, também, perpendiculares entre si. Assim, basta considerar o campo elétrico e as suas componentes nos eixos \(x\) e \(y\) escolhidos arbitrariamente nesse plano, sendo ortogonais entre si. Estas componentes obtêm-se tomando a parte real de \(\vec{E}=\vec{E}_0e^{ikz-i\omega t}\), onde \(0\vec{E}_0\) é a amplitude complexa podendo escrever-se \(\vec{E}_0=\left ( \vec{E}_{0x}e^{i\alpha},E_{0y}e^{i\beta},0 \right )\), com as amplitudes reais \(E_{0x}\) e \(E_{0y}\). Deste modo, tem-se:
\(E_{x}=E_{0x}\cos\left ( kz-\omega t+\alpha \right )\)
\(E_{y}=E_{0y}\cos\left ( kz-\omega t+\beta \right )\)
Considerando vários casos particulares da diferença \(\alpha - \beta\), definem-se vários estados de polarização. Assim:
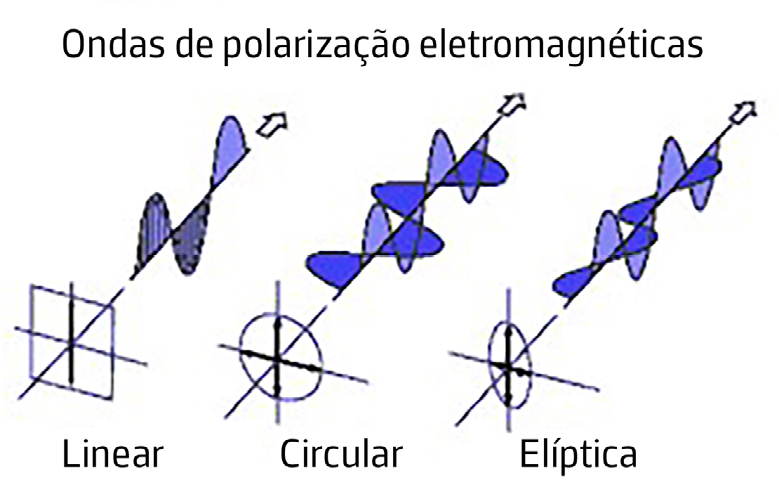
i) Se \(\alpha-\beta=0\) ou \(\alpha-\beta=\pi\), a polarização é retilínea pois que, em ambos os casos, o vetor \(\vec{E}\) vibra segundo um segmento de reta ao longo do tempo. Com efeito, é \(\frac{E_y\left ( t \right )}{E_x\left ( t \right )}=\pm \frac{E_{0y}}{E_{0x}}\).
ii) Se \(E_{0x}=E_{oy}\equiv E_0\) e \(\alpha-\beta=\pm \frac{\pi}{2}\), a extremidade do vetor \(\vec{E}\) descreve uma circunferência e a polarização diz-se circular. Com efeito, tem-se \(E_{x}^{2}\left ( t \right )+E_{y}^{2}\left ( t \right )=E_{0}^{2}\). Esta rotação pode ser no sentido direto \(\left ( \alpha-\beta=-\frac{\pi}{2} \right )\) ou no sentido retrógrado \(\left ( \alpha-\beta=\frac{\pi}{2} \right )\) para um observador alinhado com o eixo \(z\). No primeiro caso tem-se polarização circular esquerda e no segundo caso polarização circular direita.
iii) No caso geral, a extremidade do vetor \(\vec{E}\) descreve uma elipse e a polarização diz-se elíptica.
Estes três casos estão representados na FIGURA 6.
Designa-se por luz coerente a radiação onde as fases \(\alpha\) e \(\beta\) se mantêm estritamente constantes. Em contraste, se estas fases flutuarem independente e aleatoriamente, embora se mantenham constantes durante largos períodos da onda, diz-se que se trata de luz natural.
Energia e momento.
Uma onda eletromagnética transporta energia e momento que são expressões bilineares na amplitude do campo[6], pelo que é necessário considerar as expressões reais para tais amplitudes. Para uma onda monocromática e plana, é habitual definir a média sobre um ciclo de oscilação, o que muito facilita a obtenção dos resultados. Para simplificar, considere-se uma onda a propagar-se, num meio dielétrico, segundo o eixo \(z\) e linearmente polarizada segundo o eixo \(x\). Usando as equações (14) e (20), facilmente se obtém para a densidade e fluxo de energia:
\(\left \langle u \right \rangle=\frac{1}{2}\varepsilon E_{0}^{2}\) (22)
Dada a transversalidade da onda, o fluxo de energia coincide com a direção de propagação da onda, obtendo-se:
\(\left \langle S_z \right \rangle=\frac{1}{2}\varepsilon _0c\eta E_{0}^{2}\) (23)
Genericamente, um raio de luz é um grupo de ondas com a mesma frequência e que apresenta uma distribuição contínua de fluxos de energia no interior de um cone de pequena abertura. Em meios isotrópicos, este grupo de ondas também apresenta uma distribuição contínua de vetores de onda, todos da mesma grandeza, no interior do mesmo cone.
A densidade de momento do campo reduz-se à sua componente na direção de propagação, tendo-se:
\(\left \langle g_z \right \rangle=\left ( \frac{\eta}{c} \right )^2\left \langle S_z \right \rangle\) (24)
O tensor das tensões eletromagnéticas, \(\tau _{ij}\), tem nulas todas as componentes exceto:
\(\tau _{zz}=\left \langle u \right \rangle\) (25)
É interessante reinterpretar estes resultados para o vazio em termos da teoria quântica onde energia e momento estão associados ao conceito de fotão. Assim, sendo \(n\) a densidade de fotões, cada um com energia \(h\nu \), onde \(h\) é a constante de Planck e \(\nu=\frac{\omega}{2\pi}\) é a frequência da radiação, e momento \(p\), então escreve-se:
\(\left \langle u \right \rangle=nh\nu\)
e:
\(\left \langle g_z \right \rangle=np\)
Usando as equações (22) e (24), é imediato obter:
\(p=\frac{h\nu}{c}=\frac{h}{\lambda}\)
onde \(\lambda=\frac{2\pi}{k}\) é o comprimento de onda. A expressão anterior, relacionando o momento do fotão e a frequência da radiação, foi obtida por Einstein (1916).
Reflexão e refração.
A FIGURA 8 representa dois meios separados por uma superfície plana. O meio acima da superfície (meio 1) é um dielétrico onde se propaga uma onda eletromagnética de frequência \(\omega\) e vetor de onda \(\vec{k}^{\left ( i \right )}\) para a qual o meio apresenta o índice de refração \(\nu_1\). O meio 2 pode ser outro dielétrico, com índice de refração \(\nu_2\), ou um metal com uma condutividade conhecida. O plano de incidência é o plano definido pela normal à superfície (eixo \(y\)) e o vetor \(\vec{k}^{\left ( i \right )}\). Este plano corta a superfície de separação segundo o eixo \(x\).
Os campos elétrico e magnético da onda incidente actuam sobre as cargas do segundo meio, originando ondas que se propagam nos dois meios, designando-se por onda refletida a parte que se propaga no meio 1 e por transmitida a parte que se propaga no meio 2. Por que só existem estas duas ondas? Na superfície de separação \(\left ( y=0 \right )\) devem ser satisfeitas as relações de passagem, relações lineares entre componentes do campo de um e outro lado do plano.
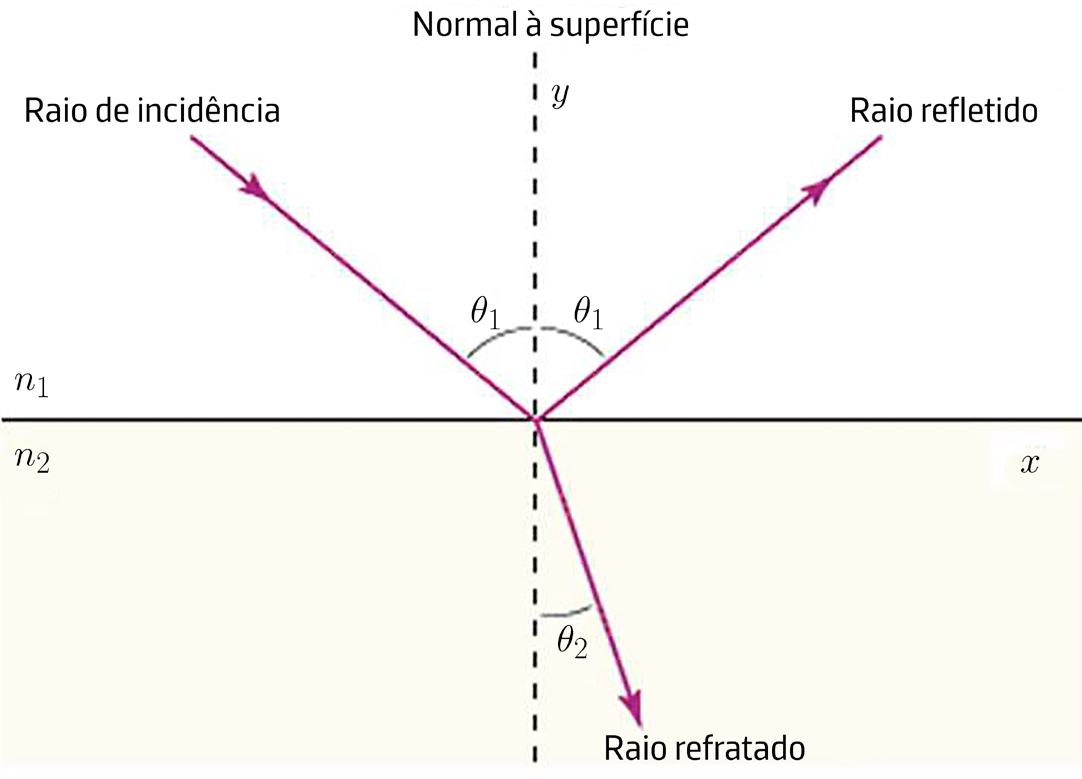
Essas relações reduzem-se a duas equações independentes e a sua satisfação exige a presença daquelas duas ondas2. Considere-se, por exemplo, a continuidade da componente tangencial do campo elétrico. Para a onda incidente, esta componente apresenta, no plano, a forma \(E_{x}^{\left ( i \right )}e^{ik_{x}^{\left ( i \right )}x-i\omega t}\). Para que aquela relação seja satisfeita em todos os instantes e em todos os pontos do plano o fator \(e^{ik_{x}^{\left ( i \right )}x-i\omega t}\) deve ser comum às ondas refletida e transmitida. Tem-se, assim que as três ondas têm a mesma frequência e que os respetivos vetores de onda satisfazem a condição:
\(k_{x}^{\left ( i \right )}=k_{x}^{\left ( r \right )}=k_{x}^{\left ( t \right )}\) (26)
Ora, a onda refletida propaga-se no mesmo meio que a onda incidente, obedecendo, pois, à mesma relação de dispersão, pelo que \(\left [ \vec{k}^{\left ( i \right )} \right ]^2=\left [ \vec{k}^{\left ( r \right )} \right ]^2\). Este resultado e a equação anterior determinam \(k_{y}^{\left ( r \right )}=-k_{y}^{\left ( i \right )}\) o que significa ser o ângulo de incidência igual ao ângulo de reflexão.
Considerando, agora, a onda transmitida, convém separar a discussão atendendo à natureza do meio 2: um dielétrico ou um condutor.
a) Para um dielétrico transparente, as equações (20) e (21) reescreve-se sob a forma:
\(\vec{k}^2=\eta^2\frac{\omega^2}{c^2}\) (27)
onde \(\eta\) é o índice de refração do meio. Aplicando ao segundo meio e tendo em conta a equação (26), tem-se:
\(\left [ k_{x}^{\left ( i \right )} \right ]^2+\left [ k_{y}^{\left ( t \right )} \right ]^2=\eta_{2}^{2}\frac{\omega^2}{c^2}\)
Da FIGURA 8, tira-se \(k_{x}^{\left ( i \right )}=k^{\left ( i \right )}\textrm{sen}\theta_1\), pelo que:
\(\left [ k_{y}^{\left ( t \right )} \right ]^2=\eta_{2}^{2}\frac{\omega^2}{c^2}-\left [ k^{\left ( i \right )}\textrm{sen}\theta_1 \right ]^2=\frac{\omega^2}{c^2}\left [ \eta_{2}^{2}-\eta_{1}^{2}\left ( \textrm{sen}\theta_1 \right )^2 \right ]\) (28)
onde se usou a equação (27) para o meio 1. Dois casos podem agora acontecer:
1º Se \(\eta_2>\eta_1\), como acontece para uma interface ar-água \(\left ( \eta=\frac{4}{3} \right )\) ou ar-vidro \(\left ( \eta=\frac{3}{2} \right )\) onde o ar é o meio 1, a equação anterior mostra que \(k_{y}^{\left ( t \right )}\) é real, podendo, então, escrever-se sob a forma (ver FIGURA 8): \(k_{y}^{\left ( t \right )}=k^t\cos\theta_2=\frac{\omega}{c}\eta^2\cos\theta_2\), obtendo-se, assim, a lei de Snell para a refração:
\(\eta_2\textrm{sen}\theta_2=\eta_1\textrm{sen}\theta_1\) (29)
2º Se \(\eta_2\) < \(\eta_1\) (os mesmos exemplos, mas trocando posições), vê-se que a lei de Snell é válida para \(\theta_1\leq \theta_L\) sendo este o ângulo limite para o qual é \(\theta_2=\frac{\pi}{2}\), i.e.
\(\textrm{sen}\theta_L=\frac{\eta_2}{\eta_1}\) (30)
Que acontece para um ângulo de incidência superior, \(\theta_1>\theta_L\)? A equação (28) mostra que \(k_{y}^{\left ( t \right )}\) é imaginário, devendo escrever-se:
\(k_{y}^{\left ( t \right )}=-i\frac{\omega}{c}\sqrt{\eta_{1}^{2}\left ( \textrm{sen}\theta_1 \right )^2-\eta_{2}^{2}}\)
de modo que a onda transmitida decai para o interior do meio 2 (onde é \(y <\) \(0\), na FIGURA 7). Este caso corresponde à reflexão total da onda incidente. Não há dissipação de energia, como se mostra no artigo “As relações de Fresnel” — a energia incidente encontra-se, sem perdas, na energia refletida.
Estes dois casos são exibidos na FIGURA 8 e exemplificado na FIGURA 9.
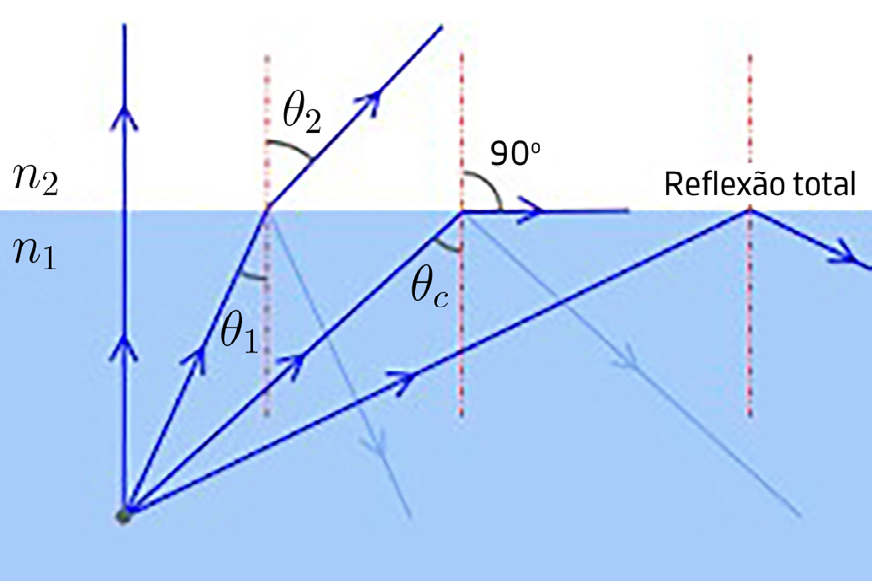

A reflexão total é usada em fibras ópticas para transmitir o sinal a grandes distâncias.
Regressando à FIGURA 7, que acontece se o meio for uma lamina de pequena espessura? A onda transmitida na primeira interface, embora atenuada, atinge a segunda interface e, se esta for seguida do mesmo meio 1 de entrada, é repetido o procedimento anterior, verificando-se a propagação da radiação para fora da segunda face (FIGURA 10) — é a reflexão total frustrada.

b) Para um meio condutor, por exemplo, um metal, a relação de dispersão é necessariamente complexa. A condutividade de um metal é da ordem de \(10^7\Omega^{-1}m^{-1}\) e \(\varepsilon _r\approx 1\). Ora, a equação (16) reescreve-se:
\(k^2=\frac{1}{c^2}\left ( \omega^2-i\omega\frac{\sigma }{\varepsilon _0} \right )\) (31)
O termo \(\frac{\sigma }{\varepsilon _0}\) é da ordem de \(10^{18}\) Hz o que determina que o termo imaginário na relação de dispersão seja muito maior que o termo real para frequências no visível (ver FIGURA 4). Assim, se o meio 2 na FIGURA 7, for um condutor, a onda transmitida é rapidamente atenuada. Aceitando que o meio 1 é o ar, tem-se:
\(\left [ k_{y}^{\left ( t \right )} \right ]^2=\left [ k^{\left ( t \right )} \right ]^2-\left ( k^{\left ( i \right )}\textrm{sen}\theta_1 \right )^2=\frac{1}{c^2}\left ( \omega^2-i\omega\frac{\sigma }{\varepsilon _0} \right )-\frac{\omega^2}{c^2}\left ( \textrm{sen}\theta_1 \right )^2\simeq -i\omega\frac{\sigma }{\varepsilon _0c^2}\)
Donde:
\(k_{y}^{\left ( t \right )}\simeq \left ( 1-i \right )\sqrt{\frac{\omega\sigma }{2\varepsilon _0c^2}}\)
A onda transmitida decai exponencialmente para o interior do meio condutor \(( y<\)\(0\) como \(e^{-\frac{\left | y \right |}{\delta}}\) onde \(\delta\) é designado por comprimento de penetração ótico:
\(\delta=\sqrt{\frac{2\varepsilon _0c^2}{\omega\sigma }}\) (32)
A FIGURA 11 mostra a dependência do comprimento de penetração com a frequência, para vários metais que, para luz visível, apresentam \(\delta\sim \) nm. Na água do mar, um eletrólito, é \(\delta\sim \) 200m para luz visível.
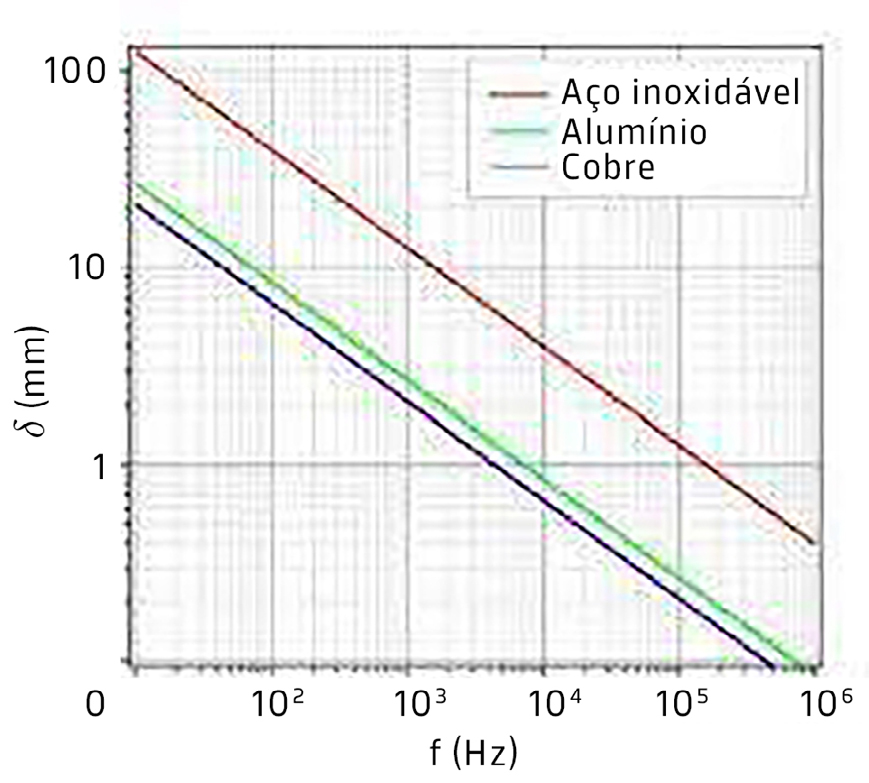
É dentro do espaço limitado pelo comprimento de penetração que ocorre o efeito Joule, a razão do decaímento da amplitude da onda transmitida. A maior parte da energia incidente encontra- se na onda refletida.
O leitor terá, certamente, percebido que todos estes resultados obtidos quer para dielétricos quer para condutores, apenas fizeram intervir a relação de dispersão. Como tal, verificam-se em muitos outros contextos onde ocorrem fenómenos ondulatórios, tal como ondas sonoras, ondas em fluidos, ondas sísmicas, etc..
Ficaram por caracterizar as amplitudes das ondas refletida e transmitida, as quais são consideradas em As relações de Fresnel.
Apêndice.
O modelo de Drude.
Considere-se uma partícula (massa \(m\), carga \(q\)) que se move sob acção de um campo elétrico constante e efetua colisões com átomos ou iões de um metal, sendo que, após cada colisão, a partícula perde memória da sua velocidade inicial. Tal partícula tem, pois, um movimento aleatório, mas com uma deriva ao longo da direção do campo. Seja \(\tau\) o tempo médio entre duas colisões sucessivas. A velocidade da partícula, ao fim deste tempo, é:
\(\vec{v}=\frac{q\vec{E}}{m}\tau\)
Após a colisão, a partícula perde memória da sua velocidade, repetindo-se o processo. Assim, se \(n\) for a densidade destas partículas, a densidade de corrente é:
\(\vec{i}=nq\vec{v}=\frac{nq^2\tau}{m}\vec{E}\)
Obtendo-se a condutividade do metal:
\(\sigma=\frac{nq^2\tau}{m}\) (33)
Referências
- ↑ LAGE, E., Os fundamentos do eletromagnetismo, Rev. Ciência Elem., V9(1):048. (2021). DOI: 10.24927/rce2021.016.
- ↑ LAGE, E., Ondas, Rev. Ciência Elem., V8(1):016. (2021). DOI: 10.24927/rce2021.016.
- ↑ LAGE, E., Polarização elétrica e magnetização, Rev. Ciência Elem., V11(1):013. (2023). DOI: 10.24927/rce2023.013.
- ↑ MAXWELL, J. C., A Dynamical Theory of the Electromagnetic Field, Phil. Trans, 166. 1865.
- ↑ LAGE, E., Campos (Física), Rev. Ciência Elem., V6(2):039. (2018). DOI: 10.24927/rce2018.039.
- ↑ LAGE, E., Polarização elétrica e magnetização, Rev. Ciência Elem., V11(1):013. (2023). DOI: 10.24927/rce2023.013.
Criada em 26 de Abril de 2022
Revista em 14 de Junho de 2022
Aceite pelo editor em 15 de Abril de 2024
