Oscilador harmónico
fReferência : Lage, E., (2019) O oscilador harmónico, Rev. Ciência Elem., V7(2):033
Autor: Eduardo Lage
Editor: José Ferreira Gomes
DOI: [http://doi.org/10.24927/rce2019.033]

O oscilador harmónico está omnipresente em Física porque é um modelo simples para fenómenos simplesmente periódicos. Aqui é estudado como objeto mecânico, o que permitirá estender muitas dos resultados ao eletromagnetismo, teoria da elasticidade, dinâmica de fluidos e, mais genericamente, ao estudo de ondas.
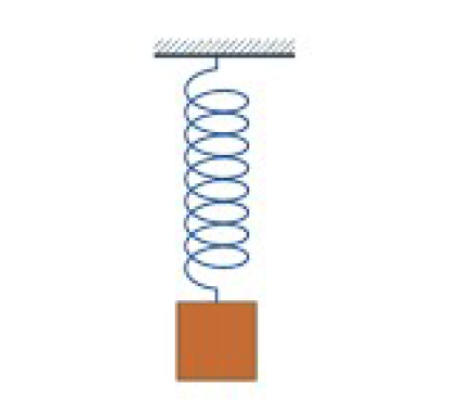
O oscilador harmónico é o dispositivo mais simples capaz de exibir um fenómeno periódico, ainda mais simples que um pêndulo, pois que este àquele se reduz para pequenas amplitudes de oscilação. Experimentalmente, é fácil construir um oscilador: uma mola suspensa verticalmente, presa no extremo superior e tendo uma pequena massa agarrada à extremidade inferior, como se exibe na FIGURA 1. Esticando a mola, aquela massa entra em oscilações periódicas tornando possível estudar e medir muitas das propriedades que, aqui, serão apresentadas.
Mas o oscilador harmónico é, também, um modelo simples para a descrição de muitos fenómenos em Física. Numa molécula diatómica, por exemplo, os átomos interagem através de um potencial que apresenta um mínimo (ver FIGURA 1 em “Equação de estado de van der Waals”), pelo que, para energias ligeiramente superiores ao mínimo, a molécula comporta-se como um oscilador harmónico. E mesmo uma molécula poliatómica pode ser modelizada como uma coleção de osciladores harmónicos, designados por modos normais de vibração, quando a energia mecânica da molécula, soma das energias cinéticas dos seus átomos com as energias de interação entre os átomos, se situa próxima do seu mínimo. O mesmo se passa num sólido que, para os efeitos aqui descritos, pode ser visualizado como uma molécula gigante. Um outro exemplo é um circuito LC, uma bobina e um condensador eletricamente conectados: o condensador descarrega carga e a consequente corrente elétrica induz uma f.e.m. na bobina, originando, assim, uma oscilação harmónica da carga e da corrente, facilmente mensuráveis por um voltímetro e um amperímetro, respetivamente. Outros exemplos surgem do comportamento elástico de materiais: uma barra horizontal, encastrada numa extremidade, apresentará oscilações harmónicas quando posta a vibrar verticalmente; um fio metálico, suspenso na vertical, também oscilará harmonicamente quando é torcido por aplicação de um momento na sua base inferior; e o mesmo fio, preso nas suas extremidades e mantido tenso, é sede de oscilações que se propagam (ver “ Campos”). Estudemos, agora, o oscilador harmónico, considerando, apenas, o caso unidimensional que servirá para apresentar os conceitos e resultados mais fundamentais. Designemos por \(x = 0\) a posição de equilíbrio do oscilador; afastada desta origem, a massa m é atuada pela força \(-kx\), onde o sinal exibe claramente que a massa é sempre puxada para a origem, quer quando a mola é esticada (\(x > 0\)), quer quando é comprimida (\(x < 0\)). A constante \(k\) é conhecida por constante da mola ou, mais geralmente, do oscilador. Se além desta força, designada por harmónica, existir uma força \(f (t)\) externamente aplicada ao oscilador, a equação de movimento fica:
\(m\frac{d^2x}{dt^2}=-kx+f(t)\) (1)
Trata-se de uma equação linear pelo que é válido o princípio da sobreposição: a soma de soluções é, ainda, uma solução. Assim, podemos estudar separadamente vários casos de interesse. Mais adiante, acrescentaremos o efeito do atrito (de Stokes), originando amortecimento, mas mantendo a linearidade da equação. Na ausência de forças externas (\(f\) = 0), a solução da eq. (1) exprime-se, simplesmente, à custa de funções trigonométricas:
\(m\frac{d^2x}{dt^2}+kx=0 \ \ \ \ \ \ \ \rightarrow \ \ \ \ \ \ \ x(t)=Acos(\omega_0t)+Bsen(\omega_0t)\) (2)
onde \(\omega_0=\sqrt{\frac{k}{m}}\) é a frequência (angular) própria do oscilador. As constantes \(A\) e \(B\) são determinadas pelas condições iniciais: designando por \(x_0\) e \(v_0\), respetivamente, a posição e velocidade iniciais, obtem-se:
\(x_0\equiv x(0)=A \\ v_0\equiv \dot{x}(0)=\omega_0B\)
Este é o movimento natural do oscilador, i.e., não sujeito a ações externas. Consideremos, agora, o efeito de forças externas. Para isso, torna-se muito mais simples e útil estudarmos o complexo \(z(t)\equiv x(t)+i\frac{v(t)}{\omega_0}\)Se conhecermos \(z (t)\), então a sua parte real é a posição atual \(x (t)\) e da sua parte imaginária deduzimos a velocidade \(v (t)\) do oscilador. Ora:
\(\frac{dz}{dt}=v(t)+\frac{i}{\omega_0}\frac{dv}{dt}=v(t)+\frac{i}{m\omega_0}\left(-kx+f\left(t\right)\right)\)
onde empregamos a eq. (1). Substituindo \(k=m\omega_0^2\).
\(\frac{dz}{dt}=v(t)-i\omega_0x(t)+\frac{i}{m\omega_0}f(t)=-i\omega_0z(t)+\frac{i}{m\omega_0}f(t)\)
Isto é:
\(\frac{dz}{dt}+i\omega_0z(t)=\frac{i}{m\omega_0}f(t)\) (3)
Esta equação é linear, pelo que se aplica o princípio da sobreposição. A solução da equação homogénea é imediata:
\(\frac{dz}{dt}+i\omega_0z(t)=0 \ \ \ \ \ \ \rightarrow \ \ \ \ \ \ z(t)=z_0e^{-i\omega_0t}\)
onde \(z_0\) é uma constante (complexa). Esta solução é o movimento natural, atrás analisado. Para, agora, encontrarmos uma solução particular da eq. (3), basta considerar \(z(t)=w(t)e^{-i\omega_0t}/\) . Substituindo na eq. (3), obtemos:
\(\frac{dw}{dt}=\frac{i}{m\omega_0}e^{i\omega_0t}f(t) \ \ \ \ \ \ \rightarrow \ \ \ \ \ \ w(t)=z_0+\frac{i}{m\omega_0}\int_{0}^{t}dt'e^{i\omega_0t'}f(t')\)
Assim, a solução geral da eq. (3) escreve-se:
\(z(t)=z_0e^{-i\omega_0t}+\frac{i}{m\omega_0}\int_{0}^{t}dt'e^{i\omega_0(t'-t)}f(t')\) (4)
O complexo \(z_0\) é inteiramente determinado pelas condições iniciais:
\(z_0=z(0)=x(0)+\frac{i}{\omega_0}v(0)\)
No que se segue, suporemos \(z_0\) = 0, concentrando-nos, pois, apenas no efeito da força aplicada.
- Comecemos por considerar o caso da força exterior constante \((f_0)\), aplicada no instante inicial – é designada por força súbita. A solução da eq. (4) é:
\(z(t)=\frac{if_0}{n\omega_0}\int_{0}^{t} dt'e^{i\omega_0(t'-t)}=\frac{f_0}{m\omega_0^2}(1-e^{-i\omega_0t})\)
Assim:
\(x(t)=Re\left[z(t)\right]=\frac{f_0}{m\omega_0^2}(1-cos(\omega_0t))\\ v(t)=Im\left[z(t)\right]=\frac{f_0}{m\omega_0}sen(\omega_0t) \)
O oscilador desloca-se harmonicamente entre a origem e a máxima amplitude \(x=\frac{2f_0}{m\omega_0^2}=\frac{2f}{k}\).
- Um segundo caso de interesse consiste em admitir que a força externa cresce muito lentamente até atingir o valor limite \(f0 -\) é designada por força adiabática. Uma expressão analítica para tal força é \(f(t)=f_0(1-e^{-\epsilon t})\), onde se considera \({\epsilon}\rightarrow 0\) no fim dos cálculos, pelo que o tempo para a força atingir o seu valor limite é da ordem de \(\frac{1}{\epsilon}\rightarrow\infty\) Inserindo na eq. (4), obtemos:
\(z(t)=\frac{if_0}{m\omega_0}\int_{0}^{t} dt'e^{i\omega_0(t'-t)}(1-e^{-\epsilon t'})= \frac{if_0}{m\omega_0}\left\{\left[\frac{1}{i\omega_0}-\frac{1}{i\omega_0-\epsilon}\right] \left[1-e^{i\omega_0t}\right]+\frac{1-e^{-\epsilon t}}{i\omega _0-\epsilon}\right\} \)
Tomando o limite \({\epsilon}\rightarrow 0\) , vem:
\(z(t)=\frac{f_0}{m\omega_0^2}=\frac{f_0}{k}\)
Vemos, assim, que a força adiabática reproduz a ideia de se manter, praticamente, o oscilador sempre em equilíbrio, levando-o até à posição final desejada, \(x=Re\left[z(t)\right]=\frac{f_0}{k}\), com velocidade nula, \(v(t)=Im\left[z(t)\right]=0\). Deste modo, o trabalho realizado pela força adiabática aparece como energia potencial elástica, \(V=\frac{1}{2}kx^2\), sendo imediato verificar que a energia mecânica \(E=\frac{1}{2}mv^2+V(x)\) se conserva na ausência de forças exteriores.
- Um terceiro exemplo considera a resposta do oscilador a uma força exteriorperiódica, i.e., \(f(t)=f_0cos(\omega t)\). Por resposta, entende-se a solução particular da eq. (3), sendo fácil verificar que tal solução é:
\(x(t)=\frac{f_0}{m(\omega_0^2-\omega^2)}cos(\omega t)\) (5)
Este importante resultado aparece em muitos domínios da Física, por exemplo na resposta de um dipólo elétrico a um campo elétrico aplicado; neste contexto, a eq. (5) fornece, diretamente, a suscetibilidade elétrica. Não escapará ao leitor que esta solução apresenta uma divergência quando a frequência da força aplicada \(\omega\) iguala a frequência própria \(\omega_0\) do oscilador, situação conhecida por ressonância. Podemos ver o que se passa regressando à eq. (4) para obter a resposta à força \(f(t)=f_0cos(\omega_0 t)\). Assim:
\(z(t)=\frac{if_0}{2m\omega_0}\int_{0}^{t} dt'e^{i\omega_0(t'-t)}\left(e^{i\omega_0t'}+e^{-i\omega_0t'}\right)= \frac{f_0}{2m\omega_0}\left(i\frac{sen\left(\omega_0t\right)}{\omega_0}+t \ cos\left(\omega_0t\right)\right)\)
Assim:
\(x(t)=\frac{f_0}{2m\omega_0}t \ sen(\omega_0t)\\v(t)\frac{f_0}{2m\omega_0}(sen(\omega_0t)+t \ cos(\omega_0t))\)
Na ressonância, posição e velocidade cresceriam sem limitações. Na prática, esta divergência não ocorre porque não podemos ignorar efeitos dissipativos tais como uma força de Stokes no meio viscoso onde o oscilador se move. Tal obriga-nos a acrescentar esta força ao 2º membro da eq. (1), que escreveremos sob a forma \(−mγv\), obtendo-se\(^1\):
\(\frac{d^2x}{dt^2}+\gamma\frac{dx}{dt}+\omega_0^2 \ x =\frac{f(t)}{m}\) (6)
Procuremos a solução particular para \(f(t)=f_0 \cos(\omega t)=Re\left[f_0e^{i\omega t}\right]\), a qual terá a forma \(x(t)=Re\left[a(\omega)e^{i\omega t}\right]\). Obtemos:
\(a(\omega)=\frac{f_0}{m}\frac{1}{\omega_0^2-\omega^2+i\gamma\omega}\) (7)
Esta resposta não é mais divergente na ressonância; ela origina uma suscetibilidade complexa nos materiais dielétricos, por exemplo. A FIGURA 2 mostra as partes real e imaginária de \(\alpha(y)\equiv \frac{m\omega_0^2}{f_0}a(\omega)\), com \(y\equiv\frac{\omega}{\omega_0}\), para fraco amortecimento, \(\frac{\gamma}{\omega_0}=0.1\). São evidentes os picos acentuados da parte imaginária na ressonância. A figura seguinte exibe as mesmas grandezas na situação de forte amortecimento, \(\frac{\gamma}{\omega_0}=10\).
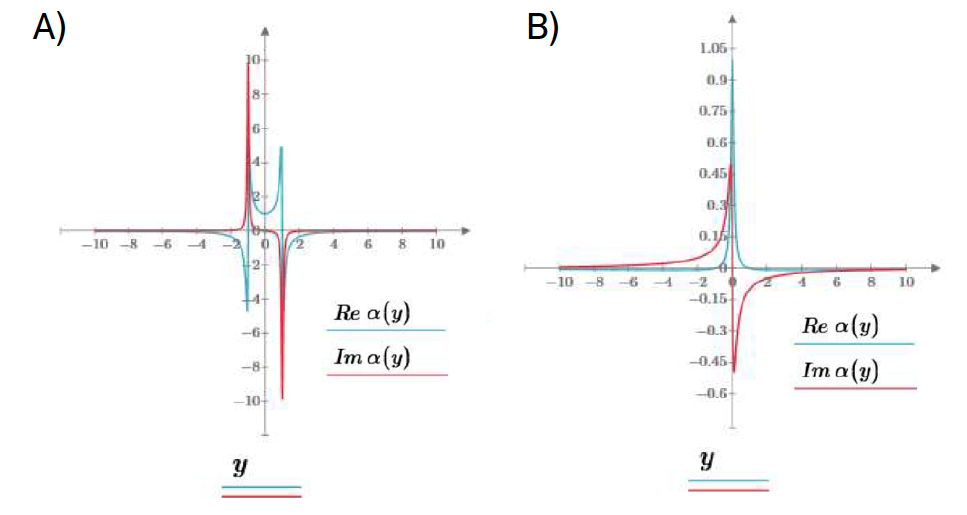
Podemos ver mais claramente a relação entre amortecimento e dissipação da energia fornecida pela força aplicada, analisando como varia a energia mecânica, atrás escrita, ao longo do tempo. Tem-se:
\(\frac{dE}{dt}=mv\left(\frac{d^2x}{dt^2}+\omega_0^2x\right)\)
Usando, agora, a eq. (6), obtemos:
\(\frac{dE}{dt}=f(t)\ v(t)-\gamma mv(t)^2\)
Efetuemos a média desta equação sobre um período da força aplicada. A média do 1º
membro é nula, porque posição e velocidade do oscilador regressam aos mesmos respetivos
valores ao fim de um ciclo. Deste modo, a média da potência da força é igual à energia
dissipada, i.e., \(\langle f(t)\ v(t)\rangle= \gamma m \langle (v(t))^2 \rangle\).
Ora,
\(v(t)=\frac{dx}{dt}=Re\left[i\omega\ a(\omega)e^{i\omega t}\right]=\omega\left[ Re\left[ a(\omega) \right]sen(\omega t)+Im\left[ a(\omega) \right]cos(\omega t)\right]\)
pelo que \(\langle f(t) \ v(t) \rangle = - \frac{f_0 \omega}{2}Im\left[a(\omega)\right] = \frac{f_0^2}{2m}\frac{\gamma\omega^2} {\left( \omega_0^2-\omega^2 \right)^2+\gamma^2 \omega^2}\geq0\).
Dissipação e parte imaginária da resposta (suscetibilidade) estão, pois, intimamente
relacionadas.
Por último, podemos analisar o comportamento do oscilador, livre de forças externas,
mas sujeito a dissipação, i.e., procurar as soluções da eq. (6) com 2º membro nulo.
Não são necessários cálculos adicionais: se existem soluções com \(f_0\) = 0, então, observando
a eq. (7), também deverá ser nulo o denominador no 2º membro desta equação,
obtendo-se, pois, as frequências naturais do oscilador:
\(\omega_0^2-\omega^2+i\gamma\omega=0 \ \ \ \ \ \rightarrow \ \ \ \ \ \ \frac{\omega_\pm}{\omega_0}=\frac{i\gamma}{2\omega_0}\pm\sqrt{1-\left(\frac{\gamma}{2\omega_0}\right)^2}\)
Assim, \(x(t)=Re\left[ A_+e^{i\omega_+t}+A_{-} e^{i\omega_{-}t} \right]\) com as constantes \(A_\pm\) determinadas pelas condições iniciais. Para fraco amortecimento, \(\frac{\gamma}{\omega_0}\ll1\), obtém-se \(\frac{\omega_\pm}{\omega_0}=\frac{i\gamma}{2\omega_0}\pm1\) que, substituídos em \(x(t)\), originam \(x(t)=e^{-\frac{\gamma t}{2}}Re\left[ A_+e^{i\omega_0t}+A_{-} e^{i\omega_{0}t} \right]\): as oscilações, têm a frequência própria, mas amortecem para 0, como se mostra na FIGURA 3.
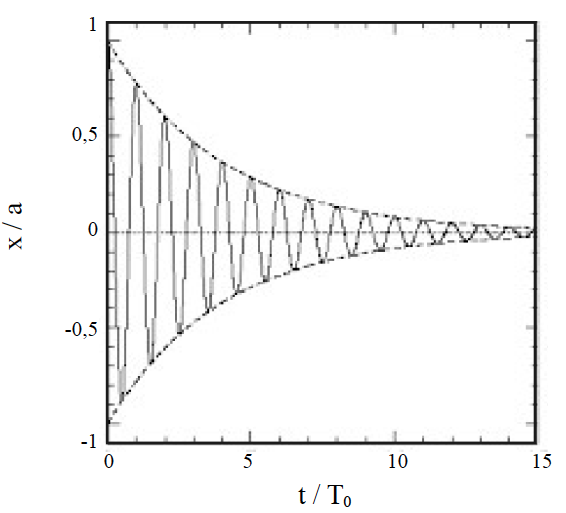
Para forte amortecimento, \(\frac{\gamma}{\omega_0}\gg1\), não há qualquer oscilação: \(\omega_+ \simeq i\gamma\) e \(\omega_{-}\simeq\frac{i\omega_0^2}{\gamma}\), \(x(t)=Re\left[ A_+e^{-\gamma t}+A_{-}e ^{\frac{\omega_0^2t}{\gamma}} \right]_ \overrightarrow{t \ \gg \ \frac{1}{\gamma}} \ Re \left[ A_{-}e^{-\frac{\omega_0^2t}{\gamma} }\right]\). A transição de amortecimento fraco para amortecimento forte dá-se para \(y = 2\omega_0 -\) é o amortecimento crítico. Neste \(x(t)=e^{-\frac{\gamma t}{2}}\left[ x_0+\left( v_0+\frac{\gamma x_0}{2} \right)t \right]\), sendo este o mais rápido decaímento, para a origem, do oscilado, rnas mesmas condições iniciais..
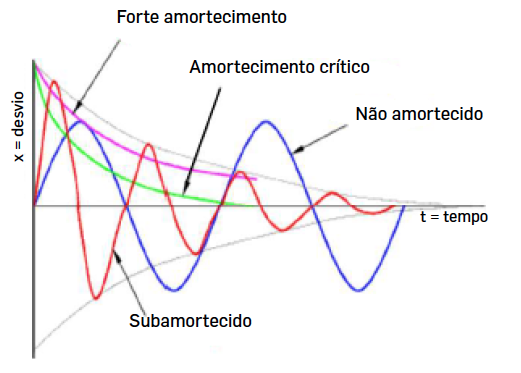
A FIGURA 4 resume todos os comportamentos do oscilador livre.
[editar] Referências
- FEYNMAN, R.P. et al. The Feynman Lectures on Physics. San Francisco: Pearson/Addison-Wesley ,Vol. 1, section 12-5, 2006. ISBN 0-8053-9049-9
- GOLDSTEIN, H. et al. Classical Mechanics, Addison Wesley 3ª edição, 2001.
- KIBBLE, T. W. B. & BERKSHIRE, F. H. , Classical Mechanics, 1966.
Recursos relacionados disponíveis na Casa das Ciências:
Criada em 5 de Junho de 2019
Revista em 5 de Junho de 2019
Aceite pelo editor em 21 de Junho de 2019
