A fórmula de Planck
Referência : Lage, E., (2020) A fórmula de Planck, Rev. Ciência Elem., V8(4):057
Autor: Eduardo Lage
Editor: José Ferreira Gomes
DOI: [https://doi.org/10.24927/rce2020.057]

[editar] Resumo
O estudo da radiação térmica foi iniciado por Kirchhoff (1860) que introduziu dois conceitos fundamentais: a intensidade espectral – a energia transportada, em cada segundo, por radiação com uma dada frequência \(\nu \) em equilíbrio térmico com matéria à temperatura absoluta \(T\) - que provou só depender da frequência e da temperatura, \(I_{\nu }\left ( T \right )\), e a noção de corpo negro, um corpo ideal que absorve toda a radiação que nele incida. A determinação desta intensidade \(I_{\nu }\left ( T \right )\) foi um problema central da Física, teórica e experimental, durante toda a segunda metade do séc. XIX. Boltzmann (1884) mostrou que a intensidade total da radiação emitida por um corpo negro é proporcional a \(T^{4}\), e Wien (1893) reduziu a intensidade espectral à forma \(I_{\nu}\left ( T \right )=\nu^{3}f\left ( \frac{\nu}{T} \right )\). Todas as tentativas para encontrar esta função universal \(f\), dentro das teorias clássicas, mostrar-se-iam não só infrutíferas como conduziam a resultados em desacordo com dados experimentais e absurdos tais como a catástrofe ultravioleta. A resolução definitiva destes problemas seria encontrada por Planck (1900) com a introdução de conceitos sem qualquer cabimento em teorias clássicas, inaugurando, dessa forma, a moderna teoria quântica.
A teoria da radiação térmica tinha aberto, em 1900, uma profunda crise na Física Clássica. Havia, por um lado, resultados que se deveriam considerar exactos como a lei de Wien para a intensidade espectral da radiação emitida por um corpo negro, à temperatura absoluta \(T\):
\(I_{\nu}=\nu ^{3}f\left ( \frac{\nu}{T} \right )\) (1)
A intensidade espectral é a energia transportada, em cada segundo, pelas ondas eletromagnéticas, de frequência \(\nu\), que constituem a radiação e, na eq. (1), a função \(f (x)\) era desconhecida. Não obstante, esta expressão para a intensidade espectral reproduzia a lei de Stefan-Boltzmann: a intensidade total radiada por um corpo negro é proporcional \(T^{4}\), um resultado verificado experimentalmente numa ampla gama de temperaturas. E também originava a lei de deslocamento de Wien: o máximo da intensidade radiada ocorre para uma frequência proporcional à temperatura absoluta. A referida crise situava-se na determinação da função \(f (x)\) quando se usavam modelos realistas, embora simplificados, para o átomo considerado como um oscilador harmónico capaz de emitir e absorver radiação. Relembremos dois importantes resultados obtidos para a densidade espectral de energia, i.e., a energia eletromagnética, por unidade de volume, associada com as ondas de frequência \(\nu\):
\(u_{\nu}\left ( T \right )=\frac{4\pi}{c}I_{\nu}\left ( T \right )=\frac{4\pi}{c}\nu^{3}f\left ( \frac{\nu}{T} \right )\) (2)
1º: A fórmula de Wien que parecia ajustar-se bem aos resultados experimentais para “altas” frequências:
\(u_{\nu}\left ( T \right )\propto \nu^{3}e^{-\frac{b\nu}{T}}\)
onde \(b\) é uma constante ajustável.
2º: A relação de Planck entre a densidade espectral e a energia média \(\left \langle E \right \rangle\), de um oscilador harmónico que troca energia com o campo de radiação:
\(u_{\nu}=\frac{8\pi\nu^{2}}{c^{3}}\left \langle E \right \rangle\) (3)
Este último resultado origina a fórmula de Rayleigh-Jeans e a consequente catástrofe ultravioleta se usarmos \(\left \langle E \right \rangle=k_{B}T\) como determinado pela Física Estatística Clássica: a radiação seria tanto mais intensa quanto maior a sua frequência sem limite superior!
Em Outubro 1900, Planck toma conhecimento dos resultados de dois grupos experimentais, em Berlim, que parecem indicar que a expressão de Wien se aproxima da previsão de Rayleigh-Jeans para “baixas” frequências. Perante estes dois limites, Planck encontra uma fórmula de interpolação que se ajusta com perfeição a todos os resultados experimentais,
\(u_{\nu}\left ( T \right )=\frac{8\pi}{c^{3}}\frac{\nu^{3}}{e^{\frac{h\nu}{k_{B}T}}-1}\), (4)
surgindo, aqui, \(h\) como uma verdadeira constante, embora de valor desconhecido, mas que serve para definir o que são “altas” temperaturas ou “baixas” frequências, antes referidas: \(\frac{h\nu}{k_{B}T}\ll 1\). Mas qual o significado físico desta fórmula que tão bem se ajusta aos dados experimentais? Usando a eq. (3), obtemos o valor médio da energia de um oscilador mecânico:
\(\left \langle E \right \rangle=\frac{h\nu}{e^{\frac{h\nu}{k_{B}T}}-1}\) (5)
Suponhamos, agora que temos \(N\gg 1\) destes osciladores – a energia média desta coleção é:
\(U=N\left \langle E \right \rangle=\frac{Nh\nu}{e^{\frac{h\nu}{k_{B}T}}-1}\)
Os osciladores trocam energia através da radiação – mas o acoplamento é feito através da carga do eletrão, quantidade suficientemente pequena para a podermos ignorar (ela não aparece na fórmula anterior) e, assim, podemos considerar o sistema de osciladores como estando praticamente isolado, com aquela energia \(U\). Qual a entropia desta coleção de osciladores? Sabemos que \(\frac{\partial S}{\partial U}=\frac{1}{T}\); assim, eliminando \(T\) através da expressão da energia \(U\) e integrando, obtemos:
\(S\left ( U,N \right )=k_{B}\left [ \left ( N+\frac{U}{h\nu} \right )log\left ( N+\frac{U}{h\nu} \right )-\frac{U}{h\nu}log\left ( \frac{U}{h\nu} \right )-NlogN \right ]\) (6)
[O último termo nesta expressão, embora irrelevante para o que se segue, é metido “à mão” para garantir a extensibilidade da entropia: \(S (xU, xN) = xS (U,N)\) para qualquer \(x > 0\)]
Passou, então, a ser este o problema de Planck: como obter esta entropia? Para o resolver, Planck vai socorrer-se da interpretação estatística de Boltzmann (que antes não aceitava): a entropia é o logaritmo (multiplicado pela constante de Boltzmann) do número de maneiras de distribuir a energia \(U\) pelos \(N\) osciladores. E faz duas hipóteses, ambas ao arrepio de qualquer interpretação clássica. Primeiro, admite que a energia \(U\) é constituída por um certo número (n) de elementos finitos de energia (\(\varepsilon \)), todos iguais (pelo que \(U = n \varepsilon\)), a que Planck deu o nome de elemento de energia (mais tarde, chamou-lhe “quantum” de energia). Isto é, Planck considera a energia disponível como se tivesse uma “estrutura atómica”, atribuindo a cada oscilador um certo número destes “átomos de energia” [O leitor não deixará de notar o “desespero” a que Planck chegara – ele tinha sérias reservas à teoria atómica da matéria!]. Segundo, embora os osciladores sejam distinguíveis, estes elementos de energia são indistinguíveis, um conceito totalmente inexistente na Física Clássica. Então, o número de maneiras de distribuir os \(n\) elementos de energia pelos \(N\) osciladores é:
\(W_{N}=\frac{\left ( N+n-1 \right )!}{n!\left ( N-1 \right )!}\)
[Este é o número de maneiras de distribuir \(n\) pontos idênticos por \(N\) caixas contíguas – cada estado possível é obtido permutando os \(n\) pontos e as \(N − 1\) paredes que dividem, internamente, as caixas, não contando como distintos quer as permutações dos pontos entre si, quer as permutações dessas paredes]. Considere-se, agora, que \(N\) e \(n\) são números grandes; usando a fórmula de Stirling para calcular o logaritmo de \(W_{N}\) e eliminar \(n\) em favor de \(U\) , obtém-se:
\(\frac{S}{k_{B}}=\left ( N+\frac{U}{\varepsilon } \right )log\left ( N+\frac{U}{\varepsilon } \right )-\frac{U}{\varepsilon }log\frac{U}{\varepsilon }-NlogN\)
Comparando com a expressão obtida para a entropia dos osciladores, eq. (6), vemos que deve ser:
\(\varepsilon =h\nu\) (7)
Quer dizer, cada oscilador só pode ter a energia \(0, h \nu, 2h \nu, ..., nh \nu, ...\) - tal é a hipótese de Planck que não encontra qualquer explicação na Física Clássica mas que se ajusta perfeitamente aos resultados experimentais relativos à intensidade espectral de um corpo negro!
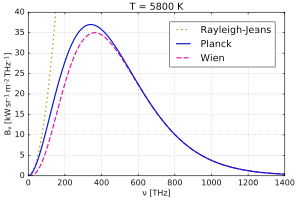
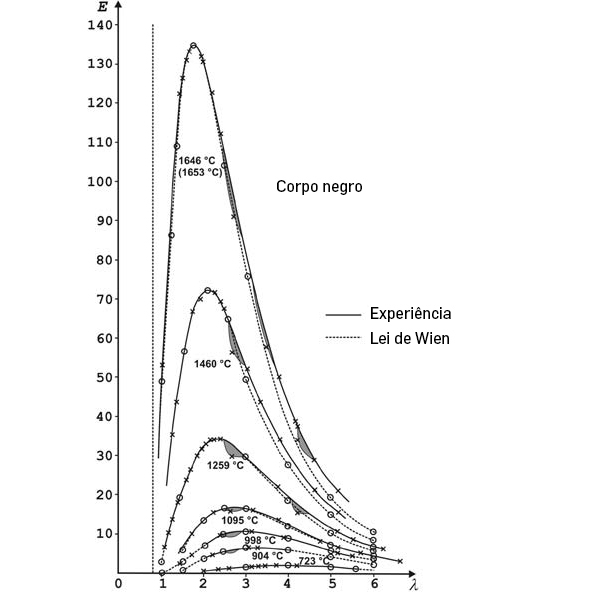
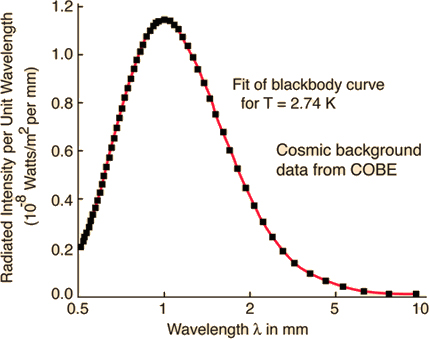
A FIGURA 1 compara as expressões para a intensidade espectral obtidas por Wien, Rayleigh-Jeans e Planck. A FIGURA 2 exibe o perfeito ajuste da intensidade espectral de Planck aos resultados experimentais obtidos em 1900. E a FIGURA 3 mostra o perfeito acordo da intensidade da radiação cósmica de fundo com a fórmula de Planck para uma temperatura \(T = 2,74K\).
Mas como determinar a constante de Planck? Relembrando a eq. (4), obtemos a forma definitiva da intensidade espectral:
\(I_{\nu}\left ( T \right )=\frac{c}{4\pi}u_{\nu }\left ( T \right )=\frac{2}{c^{2}}\frac{h\nu^{3}}{e^{\frac{h\nu}{k_{B}T}}-1}\) (8)
Planck tem a sua disposição dois resultados que lhe permitem calcular as constantes \(h\) e \(k_{B}\), nomeadamente, a constante de Stefan-Boltzmann e a lei de deslocamento de Wien). Obtém
\(h=6,55\times 10^{-34}\) Js (hoje, aceita-se \(6,63\times 10^{-34}\) Js),
que passou a ser conhecida por constante de Planck; e
\(k_{B}=1,34\times 10^{-23}\)J/K (hoje, aceita-se \(1,38\times 10^{-23}\) J/K).
A partir deste valor da constante de Boltzmann, Planck determina o número de Avogadro e, usando a constante de Faraday (\(F = 96, 500 C\)), deduz a carga do eletrão \(q_{e}=-1,56\times 10^{-19}C\) (hoje, aceita-se \(1,60\times 10^{-19}C\)). Esta observação é importante: em 1897, apenas 3 anos antes, Thomson encontrara \(q_{e}=-2,16\times 10^{-19}C\) para a carga do eletrão. Só em 1908, com a determinação, por Rutherford, da carga de uma partícula \(\alpha\) se tornou notório como era excelente o resultado de Planck.
Apesar destes excelentes resultados, apresentados em Dezembro de 1900, a hipótese de Planck foi encarada, apenas, como uma habilidade matemática, pouco convincente como teoria física. Teria que se aguardar por 1905, quando Einstein usa a teoria de Planck para conceber o “quantum” de luz, e por 1913, quando Bohr incorpora o quantum no seu modelo atómico. Cada um destes desenvolvimentos merece um tratamento próprio a considerar em futuras publicações.
[editar] Referências
- LAGE, E. A radiação térmica, Rev. Ciência Elem., V8(3):032. (2020). DOI: 10.24927/rce2020.032.
Criada em 10 de Fevereiro de 2020
Revista em 11 de Abril de 2020
Aceite pelo editor em 15 de Dezembro de 2020
