Referência : Tavares, J., Geraldo, A., (2015) Seno de um ângulo agudo, Rev. Ciência Elem., V3(1):016
Autores: João Nuno Tavares e Ângela Geraldo
Editor: José Francisco Rodrigues
DOI: [http://doi.org/10.24927/rce2015.016]

Definição

		Para definir o seno de um ângulo agudo de amplitude $\alpha\in ]0,90º[$ , fazemos a construção seguinte que se ilustra no applet escolhemos um ponto qualquer $C$ num dos lados do ângulo. Por exemplo, no applet, escolhemos o ponto $C$ num dos lados do ângulo (no applet escolhemos o lado horizontal); construímos a perpendicular a esse lado que passa em $C$ ; essa perpendicular intersecta o outro lado em $B$ e, desta forma, obtemos o triângulo retângulo representado na figura - o triângulo $ACB$ , retângulo em $C$ . O seno de $\displaystyle\alpha$ define-se agora através da razão $\sin\alpha=\displaystyle \frac{a}{c}$ onde $a$ é o comprimento do cateto $BC$ e $c$ é o comprimento da hipotenusa $AB$ . No applet pode escolher o valor de $\displaystyle\alpha$ com o cursor (a verde, à esquerda na figura). Note ainda que o valor de $\displaystyle\sin\alpha$ não depende do ponto $C$ escolhido no passo nº1 (pode verificar isso, variando a posição de $C$ no applet). De facto, variando $C$ obtemos triângulos retângulos, semelhantes entre si, e portanto, a razão $\displaystyle \frac{a}{c}$ não muda.

Nota:

Para qualquer ângulo agudo de amplitude $\alpha\in ]0,90º[$ , $0 < \sin\alpha <1$ .

Exemplos

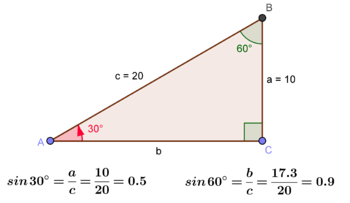
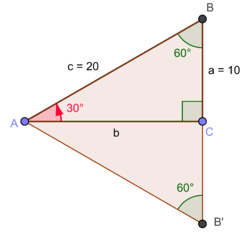
Para calcular o seno de um ângulo agudo podemos pois usar um triângulo retângulo qualquer. Por exemplo, na figura 1 usamos um triângulo retângulo cuja hipotenusa é $c=20$ , para calcular o seno de $30º$ . Como é claro da figura 2 (justifique), o cateto $a$ é metade da hipotenusa, isto é, $a=10$ e portanto

$\displaystyle \sin 30º= \frac{10}{20}=\frac{1}{2}$

Por outro lado, pelo teorema de Pitágoras, $c^2=a^2+b^2$ , e substituindo os valores de $c=20$ e $a=10$ , obtemos $b=\sqrt{400-100}=10 \sqrt{3}$ . Portanto

$\displaystyle \sin 60º= \frac{b}{c}=\frac{10 \sqrt{3}}{20}= \frac{\sqrt{3}}{2}$

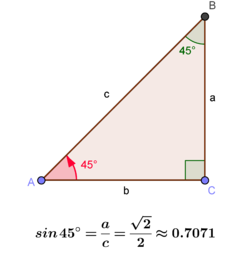
Na figura 3 usamos um triângulo retângulo isósceles (os dois catetos com o mesmo comprimento, $a=b$ ), para calcular o seno de $45º$ . Pelo teorema de Pitágoras $c^2=a^2+b^2=2a^2$ , uma vez que $a=b$ . Portanto, $c=\sqrt{2}a$ e daí que