Polarização elétrica e magnetização

Referência : Lage, E., (2023) Polarização elétrica e magnetização., Rev. Ciência Elem., V11(3):013
Autor: Eduardo Lage
Editor: João Nuno Tavares
DOI: [https://doi.org/10.24927/rce2023.013]

---

Resumo

A matéria é feita de átomos e moléculas com cargas e correntes que interagem com campos elétricos ou magnéticos e originando, por sua vez, campos que se sobrepõem aos aplicados, determinando o campo total. A polarização elétrica e a magnetização são grandezas estatísticas construídas a partir de modelos atómicos e que ajudam a caracterizar as propriedades dos meios que, nos casos mais simples, respondem linearmente aos campos aplicados. As equações de Maxwell são modificadas ao incorporarem aquelas grandezas, focando-se apenas nas cargas e correntes livres controladas nas experiências. Assim modificadas, as novas equações de campo ainda possibilitam a formulação de leis gerais de conservação da energia e do momento associadas, agora, apenas ao trabalho e força exercidos sobre as cargas e correntes livres.

Polarização.

Um meio polarizável é uma substância constituída por átomos ou moléculas que apresentam um alinhamento dos seus dipolos elétricos, seja espontaneamente (piroelétricos, e.g., turmalina, GaNiO, KH₂PO₄), abaixo de uma temperatura crítica, seja por ação de um campo elétrico exterior (moléculas apolares, e.g., O₂, H₂, ou polares, e.g., H2O). Dessa forma, originam um campo elétrico macroscópico que se adiciona ao aplicado para definir um campo total o qual contribui para o alinhamento microscópico. A polarização elétrica, \(\vec{P}\), é a média sobre um pequeno volume \(\delta V\) desses momentos dipolares:

\(\vec{P}\left ( \vec{r} \right )\delta V=\sum_{i}^{}\vec{p}_i\) (11)

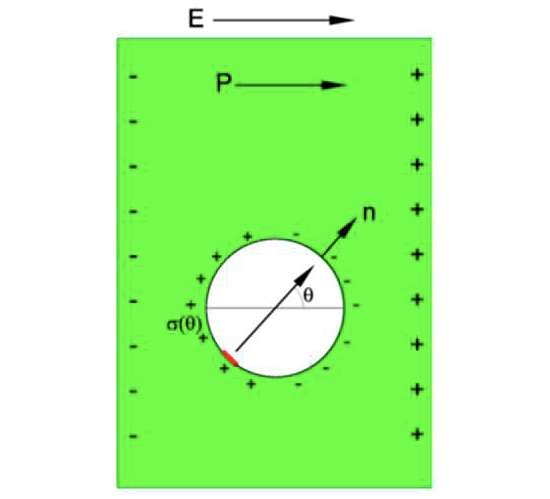
Aqui, \(\delta V\) deve entender-se como um volume macroscopicamente pequeno, centrado em ⃗\(\vec{r}\), mas que contém um número muito elevado de dipolos para se poderem ignorar as flutuações estatísticas na soma dos dipolos nele contidos (segundo membro da equação (1)). Imaginando cada dipolo como sendo ideal (i.e., duas cargas \(\pm q\) separadas por \(\vec{\delta}\) de modo que \(\vec{p}=q\vec{\delta}\)), é fácil concluir que aparece carga (dita de polarização) na superfície que separa dois meios diferentes (FIGURA 1).

FIGURA 1. Polarização e cargas superficiais.

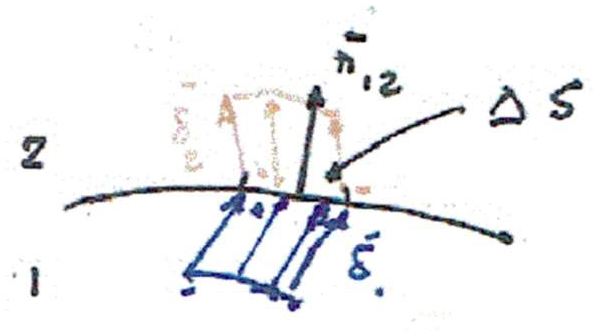
Prestando atenção ao pequeno cilindro oblíquo no meio 1, de volume \(\Delta S\vec{\delta}_1\cdot\vec{n}_{12}\), vê-se que todas as moléculas contidas neste volume depositam carga positiva na superfície. Designando por \(n_1\) o número de moléculas por unidade de volume, a carga depositada é \(n_1q_1\Delta S\vec{n}_{12}\cdot\vec{\delta}_1=\vec{P}_1\cdot\vec{n}_{12}\Delta S\). Raciocínio idêntico para o meio 2, leva ao aparecimento de carga negativa \(-\vec{P}_2\cdot\vec{n}_{12}\Delta S\) naquele elemento de superfície. Assim, a densidade superficial de cargas de polarização na superfície de separação é:

\(\rho_{S}^{\left ( P \right )}=\left ( \vec{P}_1-\vec{P}_2 \right )\cdot\vec{n}_{12}\) (2)

Considerando apenas o meio 1, supondo que está limitado por uma superfície fechada \(\Sigma\), a deposição de carga nesta superfície significa que existe carga de polarização no seu interior. A carga total que tal meio depositou na superfície é \(Q_{1}^{(P)}=\int_{\Sigma}^{}dS\vec{n}_{12}\cdot\vec{P}_1\), de modo que no interior fica a carga \(-\int_{\Sigma}^{}dS\vec{n}_{12}\cdot\vec{P}_1=-\int dV\bigtriangledown \cdot\vec{P}_1\), pelo teorema de Gauss. Assim, define-se a densidade volúmica de carga de polarização:

\(\rho^{(P)}=-\bigtriangledown \cdot\vec{P}\) (3)

Estas cargas de polarização conservam-se separadamente de outras cargas porque cada dipolo mantem unidas as cargas \(\pm q\). Ora, usando a equação (3), tem-se:

\(\frac{\partial \rho^{\left ( P \right )}}{\partial t}=-\bigtriangledown \cdot\frac{\partial\vec{P}}{\partial t}\)

levando à identificação de uma densidade de corrente de polarização:

\(\vec{i}^{\left ( P \right )}=\frac{\partial \vec{P}}{\partial t}\) (4)

É habitual separar as cargas e correntes de polarização das cargas e correntes livres sendo estas as que se controlam em experiências. Assim, a densidades decarga e corrente totais ficam:

\(\rho=\rho^{\left ( l \right )}+\rho^{\left ( P \right )}\)

\(\vec{i}=\vec{i}^{\left ( l \right )}+\vec{i}^{\left ( P \right )}\)

Substituindo a primeira relação na equação de Maxwell-Coulomb, tem-se:

\(\bigtriangledown \cdot\vec{E}=\frac{1}{\varepsilon _0}\left ( \rho^{\left ( l \right )}+\rho^{\left ( P \right )} \right )=\frac{1}{\varepsilon _0}\left ( \rho^{\left ( l \right )}-\bigtriangledown \cdot \vec{P} \right )\)

Define-se o vector deslocamento elétrico por:

\(\vec{D}=\varepsilon _0\vec{E}+\vec{P}\) (5)

obtendo-se:

\(\bigtriangledown \cdot\vec{D}=\rho^{\left ( l \right )}\) (6)

O deslocamento elétrico é inteiramente determinado pelas cargas livres.

Quanto às correntes, substituindo a decomposição anterior na equação de Maxwell-Ampère, obtém-se:

\(\bigtriangledown \wedge \vec{B}=\mu_0\left ( \vec{i}^{\left ( l \right )}+\vec{i}^{\left ( P \right )}+\varepsilon _0\frac{\partial\vec{E}}{\partial t} \right )=\mu_0\left ( \vec{i}^{\left ( l \right )}+\frac{\partial\vec{D}}{\partial t} \right )\) (7)

Considere-se, agora, o trabalho realizado pelo campo sobre as cargas livres:

\(\frac{\delta W}{\delta t}=\int dV\vec{i}^{\left ( l \right )}\cdot\vec{E}=-\int dV\vec{i}^{\left ( l \right )}\cdot\bigtriangledown \varphi=-\int dV\bigtriangledown \cdot\left ( \vec{i}^{\left ( l \right )}\varphi \right )+\int dV\varphi\bigtriangledown \cdot\vec{i}^{\left ( l \right )}\)

No último membro, o primeiro termo, sendo um integral sobre todo o espaço, anula-se (teorema de Gauss); quanto ao segundo, a conservação das cargas livres, dá:

\(\frac{\delta W}{\delta t}=-\int dV\varphi\frac{\partial \rho^{\left ( l \right )}}{\partial t}=-\int dV\varphi\bigtriangledown \cdot\left ( \frac{\partial\vec{D}}{\partial t} \right )=\)

\(=-\int dV\bigtriangledown \cdot\left ( \varphi\frac{\partial\vec{D}}{\partial t} \right )+\int dV\bigtriangledown \varphi\cdot \frac{\partial\vec{D}}{\partial t}\)

onde, de novo, se utiliza o teorema de Gauss para eliminar o penúltimo integral (divergência). Assim, obtém-se:

\(\frac{\delta W}{\delta t}=-\int dV\vec{E}\cdot\frac{\partial\vec{D}}{\partial t}\) (8)

Este importante resultado tem várias consequências que serão analisadas adiante. No que se segue, apenas se consideram meios não polarizados na ausência de um campo elétrico aplicado.

A natureza do meio determina a relação entre a polarização e o campo elétrico no seu interior. Na maior parte dos casos essa relação é linear e faz intervir o tensor susceptibilidade elétrica:

\(P_i=\varepsilon _0\chi_{ij}E_j\) (9)

(Nesta expressão, está implícita uma soma sobre índices repetidos). Em meios anisotrópicos, esta relação é responsável pelos fenómenos de birrefringência óptica (aragonite, calcite) que aqui não serão desenvolvidos. Nos meios isotrópicos (gases, líquidos, cristais do sistema cúbico), a relação anterior simplifica-se na forma que passará a ser usada:

\(\vec{P}=\varepsilon _0\chi_e\vec{E}\) (10)

No Apêndice 1 é apresentado um modelo simples para a susceptibilidade elétrica, \(\chi_e\).

Substituindo a relação (10) na equação (5), obtém-se:

\(\vec{D}=\varepsilon _0\left ( 1+\chi_e \right )\vec{E}\equiv \varepsilon \vec{E}\) (11)

onde \(\varepsilon\) é a permitividade elétrica do meio (a permitividade relativa, \(\varepsilon_r\equiv \varepsilon/\varepsilon_0\), tem valores da ordem da unidade nos gases e 80, na água, 75 no gelo, 26 no álcool etílico, 21 na acetona). Usando este resultado na equação (8), vê-se que o trabalho do campo deriva de uma energia elétrica definida em todo o espaço:

\(U_e\equiv \int dV\frac{1}{2}\varepsilon \vec{E}^2\; \; \; \; \; \rightarrow \; \; \; \; \; \; \delta W=-dU_e\) (12)

Pode ser dada uma outra forma a esta energia elétrica que torna transparente a sua relação com as cargas livres:

\(U_e=\frac{1}{2}\int dV\vec{E}\cdot\vec{D}=-\frac{1}{2}\int dV\bigtriangledown \varphi\cdot\vec{D}=-\frac{1}{2}\int dV\bigtriangledown \cdot\left ( \varphi\vec{D} \right )+\frac{1}{2}\int dV\varphi\bigtriangledown \cdot\vec{D}\)

O penúltimo termo anula-se (teorema de Gauss), obtendo-se, pela equação (6):

\(U_e=\frac{1}{2}\int dV\varphi\rho^{\left ( l \right )}\) (13)

A FIGURA 2 mostra um condensador plano submetido a uma diferença de potencial constante, \(V\).

FIGURA 2. Condensador plano parcialmente preenchido por dielétrico.

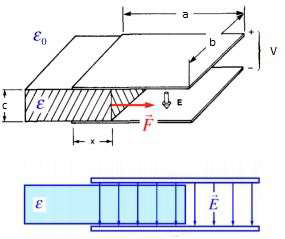
Um meio dielétrico é parcialmente introduzido no condensador, até uma distância x do bordo de entrada. Sejam \(a\) e \(b\) as dimensões das placas, e \(c\) a distância entre elas. O campo elétrico no interior do condensador, ignorando efeito de bordos, é \(E=\frac{V}{c}\), obtendo-se, assim, para o deslocamento elétrico:

\(D=\left\{\begin{matrix} \varepsilon E\;\textrm{entre}\;0\;x\\ \varepsilon_0 E\;\textrm{entre}\;x\;a \end{matrix}\right.\)

A carga livre não se distribui, pois, uniformemente nas placas, tendo-se:

\(Q(x)=\varepsilon Ebx+\varepsilon _0Eb\left ( a-x \right )\)

originando a capacidade:

\(C(x)=\frac{Q(x)}{V}=\frac{b}{c}\left ( \varepsilon x+\varepsilon _0\left ( a-x \right ) \right )\)

A energia eletrostática é, pela equação (13):

\(U_e=\frac{1}{2}C(x)V^2\)

Qual a força \(F\) que o campo elétrico exerce sobre o dielétrico? Imagine-se que o dielétrico é deslocado de \(\delta x\), de modo que a força realiza o trabalho \(F\delta x\). Mas este não é todo o trabalho realizado pelo campo sobre as cargas livres porque tal deslocamento altera a carga do condensador, \(\delta Q(x)=V\frac{dC}{dx}\delta x\); este excesso é transportado através da bateria exterior, do cátodo para o ânodo, pelo que o campo realiza o trabalho adicional \(-V\delta Q(x)\). Assim, pela equação (12), tem-se:

\(F\delta x-V^2\frac{dC}{dx}\delta x=-dU_e=-\frac{1}{2}V^2\frac{dC}{dx}\delta x\rightarrow F=\frac{1}{2}V^2\frac{dC}{dx}=\frac{V^2b}{2c}\left ( \varepsilon -\varepsilon _0 \right )\)

O dielétrico é puxado para o interior do condensador. Note-se que a origem desta força resulta da não uniformidade do campo junto aos bordos do condensador, como se mostra na FIGURA 3.

FIGURA 3. A força sobre o dielétrico tem origem no efeito de bordo.

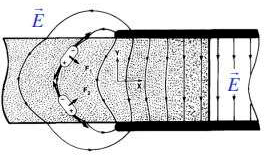
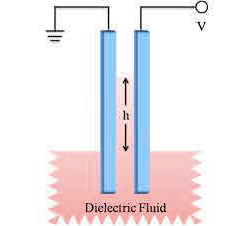
Este exemplo explica um método experimental para determinar a permitividade elétrica de um líquido (FIGURA 4). A força devida ao campo faz subir o líquido até uma altura onde é equilibrada pelo peso da coluna.

FIGURA 4. A permitividade do fluído é determinada pela altura a que sobe o liquido.

Regressando à FIGURA 3, registe-se a capacidade do condensador com o espaço entre as armaduras totalmente preenchido pelo dielétrico:

\(C=C(a)=\varepsilon \frac{ba}{c}\) (14)

Este resultado, referente a um condensador plano, estende-se a outras geometrias, bastando substituir a permitividade do vazio pela do meio dielétrico na respectiva expressão da capacidade.

A FIGURA 5 mostra uma esfera com uma polarização uniforme, \(\vec{P}\), com o sentido vertical.

FIGURA 5. Campo elétrico originado por esfera com polarização uniforme.

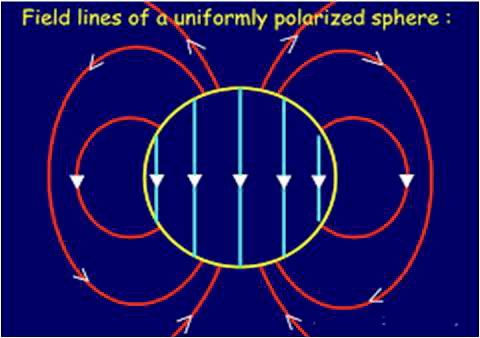
Tal significa uma carga superficial de polarização \(\rho_{S}^{\left ( P \right )}=P\cos\theta\), onde \(\theta\) é o ângulo entre a vertical e o ponto na superfície. O campo originado por tal distribuição de carga já foi considerado em “Eletrostática”: é dipolar no exterior da esfera e, dentro dela, é uniforme com o valor \(\vec{E}=-\frac{\vec{P}}{3\varepsilon _0}\). Considere-se, agora, um meio dielétrico onde existe um campo uniforme, \(\vec{E}\) . Imagine- se que, no interior deste meio, existe uma cavidade esférica (FIGURA 6). Qual o campo \(\vec{E}'\) no interior da cavidade? A resposta obtém-se por simples sobreposição: se se preencher a cavidade com a esfera da FIGURA 5, o campo naquela esfera é, por um lado, \(\vec{E}'-\frac{\vec{P}}{3\varepsilon _0}\) e, por outro lado apresenta o campo uniforme \(\vec{E}'\). Assim, é \(\vec{E}'=\vec{E}+\frac{\vec{P}}{3\varepsilon _0}\). Este campo é designado por campo local porque é ele que actua sobre uma molécula apolar, por exemplo, colocada no centro da esfera. A molécula adquire um dipolo elétrico \(\vec{p}\), como se exemplifica no Apêndice 1, sendo:

\(\vec{p}=\varepsilon _0\alpha\vec{E}\;'\)

onde \(\alpha\) é a polarizabilidade molecular. Considerando \(n\) moléculas por unidade de volume, fica encontrada a polarização elétrica:

\(\vec{P}=n\vec{p}=\varepsilon _0n\alpha\left ( \vec{E}+\frac{\vec{P}}{3}\varepsilon _0 \right )\rightarrow \vec{P}=\varepsilon _0\frac{3n\alpha}{3-n\alpha}\vec{E}\)

Usando a equação (10), deduz-se a susceptibilidade elétrica, podendo finalmente estabelecer-se a relação de Clausius-Mossotti:

\(n\alpha=\frac{3\chi_e}{3+\chi_e}=\frac{3\left ( \varepsilon _r-1 \right )}{2+\varepsilon _r}\) (15)

Este importante resultado estabelece uma ligação entre uma propriedade microscópica \((\alpha)\) e uma propriedade macroscópica \((\varepsilon)\), permitindo aferir o realismo de modelos moleculares.

FIGURA 6. Cavidade esférica num meio polarizado.

Magnetização.

Átomos ou moléculas podem apresentar momentos magnéticos ou estes serem induzidos por um campo magnético aplicado. A ordenação espacial destes momentos magnéticos em sólidos, na qual intervém a interação magnética entre dipolos, origina uma grande riqueza de estruturas ferromagnéticas ou anti-ferromagnéticas que desaparecem acima de uma temperatura crítica (ponto de Curie em ferromagnetos e ponto de Néel em antiferromagnetos). Gases e líquidos são, em geral, desprovidos de tais ordenações e só apresentam um comportamento magnético macroscópico como resposta a um campo aplicado. No que se segue, só serão consideradas estas substâncias, apresentando-se no Apêndice 2 um modelo simples para o seu comportamento.

A magnetização é a média sobre a unidade de volume dos momentos magnéticos nele contidos:

\(\vec{M}\left ( \vec{r} \right )\delta V=\sum_{i}^{}\vec{\mu}_i\) (16)

Aqui, \(\delta V\) é um pequeno volume, centrado em \(\vec{r}\), mantendo-se as observações a seguir à equação (1). A magnetização define correntes na superfície e no interior de magnetos — são correntes de natureza microscópica, não detectáveis por um amperímetro.

A FIGURA 7 representa uma porção da superfície (área \(\Delta x\Delta y\)) de um magneto onde a magnetização \(\vec{M}\) define o eixo \(y\). Considere-se o pequeno paralelepípedo (volume \(\Delta x\Delta y\Delta z\)) de que aquela pequena superfície é a face superior. O momento magnético no paralelepípedo é \(M_y\Delta x\Delta y\Delta z\) e pode ser imaginado como resultante de \(N\) espiras rectangulares, cada uma percorrida por uma corrente de intensidade \(I\), de modo que \(M_y\Delta x\Delta y\Delta z=NI\Delta x\Delta y\). Há, assim, uma corrente superficial naquela face superior: \(i_{x}^{\left ( S \right )}\Delta y=NI=M_y\Delta y\), i.e., \(i_{x}^{\left ( S \right )}=\left ( \vec{M}\wedge \vec{e}_z \right )_x\).

FIGURA 7. A face superior da superfície do magneto apresenta uma corrente superficial de magnetização.

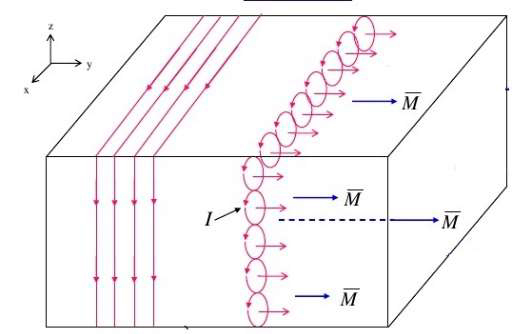
Procedendo da mesma forma para outras superfícies com diferentes normais, conclui-se genericamente que a densidade superficial de corrente de magnetização é:

\(\vec{i}_{M}^{\left ( S \right )}=\vec{M}\wedge \vec{n}\) (17)

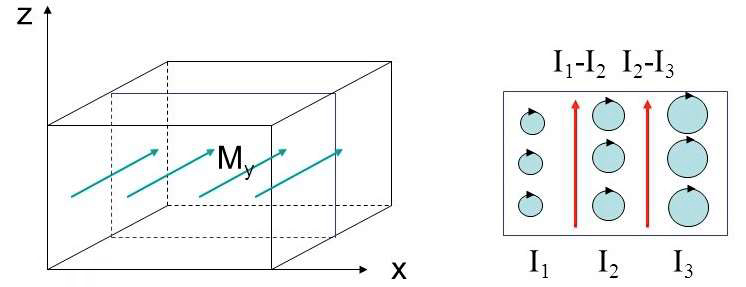
Considere-se, agora, o interior do magneto onde a magnetização é não uniforme e nele imagine- se um paralelepípedo onde a magnetização \(M_y\) cresce com \(x\), i.e., \(\frac{\partial M_y}{\partial x}>0\) (FIGURA 8).

Dividindo o paralelepípedo em células verticais, o momento magnético de cada célula pode ser considerado como resultante de espiras, sendo que a corrente, em cada espira, cresce com \(x\). Deste modo, na face comum de células contiguas passa a existir uma corrente segundo \(z\).

Repetindo o raciocínio anterior, conclui-se ser \(\left ( \vec{i}_M \right )_z=\frac{\partial M_y}{\partial x}\), um caso particular da relação genérica:

\(\vec{i}_M =\bigtriangledown \wedge \vec{M}\) (18)

FIGURA 8. Uma magnetização não uniforme gera correntes volúmicas.

Deste modo, a equação de Maxwell-Ampère fica:

\(\bigtriangledown \wedge \vec{B}=\mu_0\left ( \vec{i}^{\left ( l \right )}+\bigtriangledown \wedge \vec{M} \right )\) (19)

Defina-se o campo \(\vec{H}\) por:

\(\vec{H}=\frac{\vec{B}}{\mu_0}-\vec{M}\) (20)

A equação (19) mostra que \(\vec{H}\) é inteiramente determinado pelas correntes livres:

\(\bigtriangledown \wedge \vec{H}=\vec{i}^{\left ( l \right )}\) (21)

e pela condição, derivada da equação (20):

\(\bigtriangledown \cdot\vec{H}=-\bigtriangledown \cdot \vec{M}\) (22)

Mostrar-se-á adiante como estes resultados se reduzem, muitas vezes, às equações da Eletrostática.

O trabalho realizado pelo campo sobre as correntes livres fica:

\(\frac{\delta W}{\delta t}=\int dV\vec{i}^{\left ( l \right )}\cdot\vec{E}=\int dV\bigtriangledown \wedge \vec{H}\cdot\vec{E}=\int dV\left [ -\bigtriangledown \cdot\left ( \vec{E}\wedge \vec{H} \right )+\vec{H}\cdot\left ( \bigtriangledown \wedge \vec{E} \right ) \right ]\)

O termo com a divergência, integrado sobre todo o espaço, anula-se (teorema de Gauss) e o seguinte dá, pela lei da indução de Faraday:

\(\frac{\delta W}{\delta t}=-\int dV\vec{H}\cdot\frac{\partial \vec{B}}{\partial t}\) (23)

Os magnetos permanentes apresentam curvas de histerese (FIGURA 9): á área dentro da curva é igual ao trabalho realizado pela bateria, igual e oposto ao segundo membro da equação (23).

FIGURA 9. Curva de histerese de um ferromagneto.

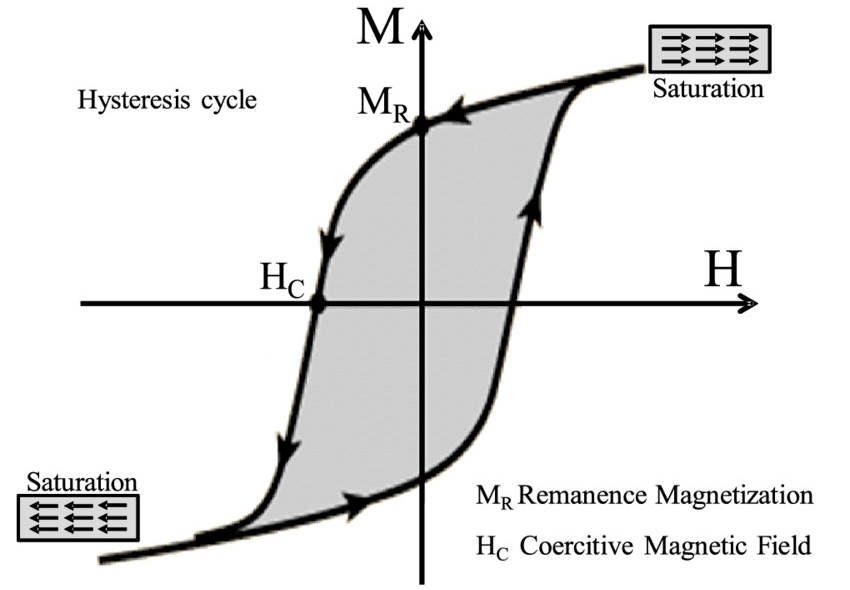
Na ausência de correntes livres, o campo \(\vec{H}\) gerado por um magneto permanente, obedece às equações da Magnetostática:

\(\bigtriangledown \wedge \vec{H}=0\rightarrow \vec{H}=\bigtriangledown \psi \)

\(\bigtriangledown \cdot\vec{H}=-\bigtriangledown \cdot\vec{M}\rightarrow \Delta \psi=-\bigtriangledown \cdot\vec{M}\)

Aqui, \(\psi\), um pseudo-escalar, é designado por potencial magnético. Estas equações são idênticas às do campo eletrostático, podendo simplesmente transpor-se muitos dos resultados aí obtidos, como a seguir se mostra. Numa superfície de separação de meios magnéticos, a continuidade da componente normal de \(\vec{B}\) impõe a continuidade de \(\left ( \vec{H}+\vec{M} \right )\cdot\vec{n}\) — os pólos norte e sul de um magneto surgem, assim, como cargas magnéticas inseparáveis.

Num íman de barra (FIGURA 10), com forma cilíndrica, de comprimento muito maior que o raio, e magnetização uniforme dirigida segundo o eixo do cilindro, as linhas de força de \(\vec{B}\) são, no exterior, semelhantes às de um dipolo magnético.

FIGURA 10. Íman de barra.

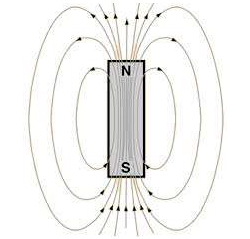
A equação (17) mostra que a magnetização pode ser entendida como correntes superficiais, circulares em torno do eixo, pelo que o campo \(\vec{B}\) é o de um solenóide, donde, no interior do magneto, é:

\(\vec{B}\approx \mu_0\vec{M}\)

Uma esfera uniformemente magnetizada (FIGURA 11), apresenta, para \(\vec{B}\), um campo uniforme no seu interior, \(\vec{H}=-\frac{\vec{M}}{3}\), e o campo dipolar magnético no exterior. A figura mostra as linhas de força dos campos \(\vec{H}\) (à esquerda) e \(\vec{B}\) (à direita).

FIGURA 11. Esfera magnetizada uniformemente.

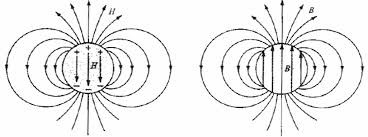
Nos materiais desprovidos de uma magnetização permanente, a aplicação de um campo magnético induz uma magnetização, definindo-se a susceptibilidade \(\chi_m\) por:

\(\vec{M}=\chi_m\vec{H}\rightarrow \vec{B}=\mu\vec{H}\; \; \; \; \; \mu=\mu_0\left ( 1+\chi_m \right )\) (24)

Aqui, μ é a permeabilidade magnética do meio. Em contraste com a susceptibilidade elétrica, a susceptibilidade magnética pode ser negativa (diamagnetismo, e.g., grafite, vidro, H₂O, H₂, He, N, Hg) ou positiva (paramagnetismo, e.g., O₂, CuSO₄, MnSO₄). Tal resulta da lei de indução de Faraday: o campo ao ser aplicado pode originar dipolos magnéticos que se lhe opõem (lei de Lenz) ou simplesmente alinhá-los. No Apêndice 2 é apresentado um modelo simples para este tipo de comportamentos.

Para tais materiais, a equação (23) permite definir uma energia magnética:

\(U_m=\frac{1}{2}\int dV\mu\vec{H}^2\) (25)

De modo que o trabalho realizado pelo campo é:

\(\delta W=-dU_m\) (26)

A FIGURA 12 mostra um cilindro de uma substância magnetizável parcialmente introduzido numa bobina (\(N\) espiras, comprimento \(l\), área transversal \(S\)) alimentada por um gerador de corrente que mantém sempre a intensidade \(I\) constante. O campo gerado por este solenóide no seu interior é \(H=\frac{NI}{l}\) — é este, também o campo na parte introduzida (comprimento \(x\)) do cilindro, por continuidade da sua componente longitudinal.

FIGURA 12. Cilindro magnetizável inserido em solenóide.

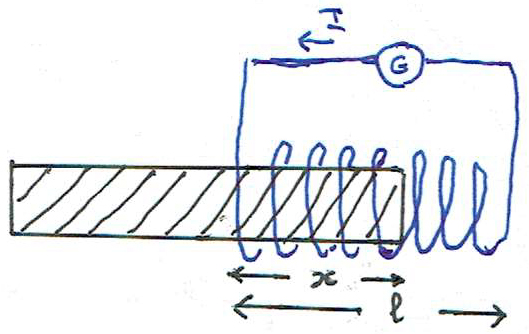
Assim, a energia magnética é:

\(U_m=\frac{1}{2}S\left [ \mu x+\mu_0\left ( l-x \right ) \right ]H^2\)

Se se deslocar o cilindro de \(\delta x\), há uma alteração de fluxo magnético nas \(\frac{N}{l}\delta x\) espiras atravessadas pelo cilindro. Ora, o fluxo do campo magnético através destas espiras era \(\mu_0 HS\frac{N}{l}\delta x\) antes do deslocamento, e \(\mu HS\frac{N}{l}\delta x\) após o deslocamento, pelo que a variação de fluxo é \(\delta\Phi =S\left ( \mu-\mu_0 \right )\frac{NH}{l}\delta x\), sendo induzida a f.e.m. \(\varepsilon =-\frac{d\Phi }{dt}\) (no gerador, esta f.e.m. é automaticamente compensada para manter constante a corrente). O campo realiza o trabalho \(I\varepsilon +F\frac{dx}{dt}\), onde \(F\) é a força que o campo exerce sobre o cilindro. Assim, usando a equação (26), obtém-se:

\(I\varepsilon +F\frac{dx}{dt}=-\frac{dU_m}{dt}\rightarrow F=\frac{1}{2}S\left ( \mu-\mu_0 \right )H^2\)

Num material paramagnético \(\left ( \mu>\mu_0 \right )\), o cilindro é puxado para o interior do solenóide; num material diamagnético \(\left ( \mu<\mu_0 \right )\), o cilindro é expelido do solenóide.

A medição experimental da susceptibilidade é esquematizada na FIGURA 13: a amostra (um pequeno cilindro de secção com área \(S\)) é parcialmente introduzida no entreferro de um íman permanente que cria um campo horizontal de intensidade a \(H\) praticamente uniforme na região de interesse.

FIGURA 13. Dispositivo para medir a susceptibilidade magnética.

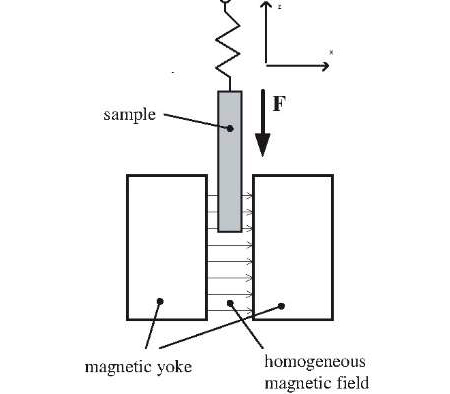
A força que actua sobre a amostra é:

\(F_z=\int dV'\vec{M}\left ( \vec{r}\;' \right )=\mu_0\int dV'\chi_m\vec{H}_a\left ( \vec{r}\;' \right )=\mu_0S\chi_m\frac{H_{a}^{2}}{2}\frac{dh}{dz}\)

onde \(h\) é a altura da parte do cilindro mergulhada no entreferro, pelo que \(\frac{dh}{dz}=-1\). Assim:

\(F_z=-\mu_0S\chi_m\frac{H_{a}^{2}}{2}\)

Esta força puxa o cilindro para o entreferro se a amostra é paramagnética \(\left ( \chi_m>0 \right )\) ou expele- -o daquela região se a amostra é diamagnética \(\left ( \chi_m&lt 0 \right )\), podendo ser medida por uma balança.

A equação (23) pode ser apresentada sob outra forma de grande utilidade. Para isso, escreve- se o campo \(\vec{H}\) como soma do campo aplicado, \(\vec{H}_a\), e do campo gerado pela magnetização que, como se mostrou atrás, deriva de um gradiente, \(\bigtriangledown \psi\). Assim aquela equação fica:

\(-\frac{\delta W}{\delta t}=\int dV\left ( \vec{H}_a+\bigtriangledown \psi \right )\cdot\frac{\partial\vec{B}}{\partial t}=\int dV\vec{H}_a+\int dV\bigtriangledown \cdot\left ( \frac{\partial\vec{B}}{\partial t} \right )\)

O termo com a divergência anula-se (teorema de Gauss). Quanto ao primeiro termo, fica:

\(\int dV\vec{H}_a\cdot\frac{\partial\vec{B}}{\partial t}=\mu_0\int dV\vec{H}_a\cdot\left ( \frac{\partial\vec{H}_a}{\partial t}+\bigtriangledown \left ( \frac{\partial\psi}{\partial t} \right )+\frac{\partial\vec{M}}{\partial t} \right )=\)

\(=\frac{d}{dt}\int dV\frac{1}{2}\vec{H}_{a}^{2}+\int dV\bigtriangledown \cdot\left ( \vec{H}_a\frac{\partial\psi}{\partial t} \right )+dV\vec{H}_a\cdot\frac{\partial\vec{M}}{\partial t}\)

No último membro, o primeiro termo é simplesmente o trabalho realizado pelo gerador, na unidade de tempo, para criar o campo aplicado, podendo ser ignorado no que segue, e o segundo termo anula-se (teorema de Gauss). Assim, a equação (23) fica:

\(\frac{\delta W}{\delta t}=-\int dV\vec{H}_a\cdot\frac{\partial\vec{M}}{\partial t}\) (27)

Esta expressão já fora obtida em “Trabalho do campo eletromagnético em dielétricos e magnetes”, embora aí se considerasse o trabalho do gerador de corrente, igual e oposto a este.

Num supercondutor de primeira espécie, o campo magnético é totalmente eliminado do seu interior abaixo de uma temperatura crítica (efeito Meissner). Em geral, é considerada uma amostra fina (agulha) do material supercondutor (\(Nb\), por exemplo), colocada paralelamente ao campo aplicado, de modo que a \(H = H_a\) dentro da agulha. Assim, na fase supercondutora, é \(H_a +M = 0\) — o supercondutor é o perfeito diamagneto. Inserindo na equação anterior, determine-se o trabalho realizado quando o campo cresce de 0 até atingir um valor crítico, \(H_{a}^{\left ( c \right )}\left ( T \right )\) que depende da temperatura e se anula na temperatura crítica. Tem-se:

\(W=\frac{1}{2}V\left [ H_{a}^{\left ( c \right )}\left ( T \right ) \right ]^2\)

onde \(V\) é o volume do supercondutor. Este trabalho deve ser igual à diferença de energia livre entre o estado inicial (supercondutor sem campo) e o estado final (estado normal com campo crítico):

\(F_n\left ( T,H_{a}^{\left ( c \right )}\left ( T \right ) \right )-F_s\left ( T,0 \right )=\frac{1}{2}V\left [ H_{a}^{\left ( c \right )}\left ( T \right ) \right ]^2\)

No estado normal, os materiais supercondutores são fracamente magnéticos, pelo que o resultado anterior se pode reescrever sob a forma:

\(F_s\left ( T,0 \right )=F_n\left ( T,0 \right )-\frac{1}{2}V\left [ H_{a}^{\left ( c \right )}\left ( T \right ) \right ]^2\)

Conclui-se, assim, que o estado supercondutor é termodinamicamente mais estável que o estado normal, para a mesma temperatura. Esta diferença de energia é, essencialmente, devida ao “gap” no espectro de energia eletrónico que se comporta como um gás de Bose, abaixo da temperatura crítica, e como um gás fermiónico livre acima dessa temperatura.

As equações de Maxwell modificadas pela matéria.

Com a separação de cargas e correntes naquelas que são livres e nas que resultam da polarização ou magnetização do meio, é agora fácil reescrever as equações de Maxwell adaptadas aos meios materiais. Assim:

\(\bigtriangledown \cdot\vec{D}=\rho^{\left ( l \right )}\) (28)

\(\bigtriangledown \wedge \vec{H}=\vec{i}^{\left ( l \right )}+\frac{\partial \vec{D}}{\partial t}\) (29)

\(\bigtriangledown \wedge \vec{E}=-\frac{\partial\vec{B}}{\partial t}\) (30)

\(\bigtriangledown \cdot\vec{B}=0\) (31)

Nos meios isotrópicos e lineares, estas relações são completadas pelas equações constitutivas do meio:

\(\vec{D}=\varepsilon \vec{E}\) (32)

\(\vec{B}=\mu \vec{H}\)

É possível deduzir leis de conservação de energia e momento para as cargas e correntes livres. O método consiste simplesmente em adaptar o modo como tais leis foram genericamente deduzidas e interpretadas em Os fundamentos do eletromagnetismo. Apresentam-se apenas os resultados:

os resultados: A) O trabalho realizado pelo campo sobre as cargas livres escreve-se:

\(\frac{\delta W}{\delta t}=\int dV\vec{i}^{\left ( l \right )}\cdot\vec{E}=-\int dV\bigtriangledown \cdot\left ( \vec{E}\wedge \vec{H} \right )-\int dV\frac{du}{dt}\) (34)

onde:

\(du=\vec{E}\cdot d\vec{D}+\vec{H}\cdot d\vec{B}\) (35)

Nos meios lineares e isotrópicos, fica definida esta densidade de energia:

\(u=\frac{1}{2}\varepsilon \vec{E}^2+\frac{1}{2}\mu \vec{H}^2\) (36)

A equação (34) também define o fluxo de energia:

\(\vec{S}=\vec{E}\wedge \vec{H}\) (37)

B) A força, por unidade de volume, que se exerce sobre cargas e correntes livres:

\(\vec{f}=\rho^{\left ( l \right )}\vec{E}+\vec{i}^{\left ( l \right )}\wedge \vec{B}\) (38)

pode escrever-se sob a forma, para uma componente genérica \(i = 1, 2, 3\):

\(f_i=-\frac{\partial g_i}{\partial t}+\frac{\partial}{\partial x_j}\left ( E_iD_j+H_iB_j \right )-D_j\frac{\partial E_j}{\partial x_i}-B_j\frac{\partial H_j}{\partial x_i}\) (39)

onde a densidade volúmica de momento é:

\(\vec{g}=\vec{D}\wedge \vec{B}\) (40)

Nos meios lineares e isotrópicos, a equação (39) reescreve-se sob a forma da divergência do tensor de Maxwell adaptado aos meios em presença:

\(f_i=-\frac{\partial g_i}{\partial t}-\frac{\partial}{\partial x_j}\tau _{ij}\) (41)

onde:

\(\tau _{ij}=u\delta_{ij}-\varepsilon E_iE_j-\mu H_iH_j\) (42)

Recorda-se que \(\tau _{ij}n_jdA\) é o momento do campo que, na unidade de tempo, atravessa a área \(dA\) no sentido da sua normal \(\vec{n}\). Como exemplo, considere-se a FIGURA 3, com o dielétrico totalmente inserido no condensador. Tomando o eixo \(x_3\equiv z\) na direcção do campo elétrico (perpendicular às armaduras), o momento transferido na unidade de tempo para a armadura superior, i.e., a força exercida nas cargas livres dessa placa, é \(\tau_{33}A=-\frac{1}{2}\varepsilon E^2\), um resultado que se pode confirmar calculando o trabalho para um deslocamento virtual daquela placa. O sinal negativo significa a atração, modificada pelo meio, que a placa inferior exerce sobre a superior.

Finalmente, notar-se-á que, nestes meios, a densidade de momento e o fluxo de energia estão relacionados:

\(\vec{g}=\varepsilon \mu\vec{S}\) (43)

Apêndice 1.

Um modelo para a polarizabilidade molecular.

O primeiro modelo para o comportamento de átomos sob ação de campos elétrico ou magnético, deve-se a H. A. Lorentz (1880). Considerem-se duas cargas \(\pm q\), com a carga positiva (núcleo) imóvel e a carga negativa (eletrão), de massa \(m\), submetida ao potencial harmónico \(\frac{1}{2}m\omega_{0}^{2}\left ( x-a \right )^2\) e à ação de um campo elétrico local \(E\), movendo-se num meio viscoso que origina uma força de Stokes \(-m\gamma\frac{dx}{dt}\). A equação de movimento da carga positiva é:

\(m\frac{d^2x}{dt^2}=-m\omega_{0}^{2}\left ( x-a \right )-m\gamma\frac{dx}{dr}+qE\)

Para um campo elétrico estático, a posição de equilíbrio desta carga ocorre para \(x =\delta\), com:

\(\delta=a-\frac{\left | q \right |E}{m\omega_{0}^{2}}\)

Assim, o momento dipolar \(p=-\left | q \right |\delta\) tem uma parte independente do campo (molécula polar), acrescida de uma resposta linear ao campo, definindo a polarizabilidade estática da molécula: \(\alpha(0)=\frac{q^2}{\varepsilon _0m\omega_{0}^{2}}\). Suponha-se, agora, que o campo elétrico varia sinusoidalmente no tempo e procure-se a resposta do oscilador. Dada a linearidade da equação de movimento, é útil considerar a representação complexa, \(E(t)=E_0e^{i\omega t}\), devendo tomar-se a parte real no fim dos cálculos. Substituindo \(x(t)=a+x_0e^{i\omega t}\) na equação de movimento, obtém-se:

\(x_0\left ( \omega \right )=\frac{-\left | q \right |E_0}{m}\frac{1}{\omega_{0}^{2}-\omega^2-i\gamma\omega}\)

Deste modo, a componente do dipolo que responde ao campo, é:

\(p=\frac{q^2E_0}{m}\frac{1}{\omega_{0}^{2}-\omega^2-i\gamma\omega}\)

Se houver \(n\) destes osciladores por unidade de volume, a polarização elétrica é:

\(P(t)=\textrm{Re}\left [ \frac{nq^2E_0e^{-i\omega t}}{m}\frac{1}{\omega_{0}^{2}-\omega^2-i\gamma\omega} \right ]\equiv \textrm{Re}\left [ \varepsilon _0\chi_e(\omega)E_0e^{-i\omega t} \right ]\)

Obtém-se assim a susceptibilidade elétrica deste sistema de dipolos:

\(\chi_e(\omega)=\frac{nq^2}{m\varepsilon _0}\frac{1}{\omega_{0}^{2}-\omega^2-i\gamma\omega}\rightarrow \varepsilon _r(\omega)=1+\chi_e(\omega)\)

A parte imaginária da susceptibilidade é responsável pela perda efectiva de energia do campo. Com efeito, para um oscilador, a potência da força exercida pelo campo é \(-\left | q \right |E(t)\frac{dx}{dt}\); para os n osciladores na unidade de volume, a potência fica \(-n\left | q \right |E(t)\frac{dx}{dt}=E(t)\frac{dP}{dt}\). Tomando a média sobre um ciclo de oscilação do campo, tem-se:

\(\left \langle \frac{\delta W}{\delta t} \right \rangle=\frac{1}{2}\textrm{Re}\left [ E^*\left ( -i\omega P \right ) \right ]=\frac{1}{2}\textrm{Re}\left [ i\omega\varepsilon _0\chi_e\left ( \omega \right )\left | E_0 \right |^2 \right ]=\frac{1}{2}\varepsilon _0\left | E_0 \right |^2\omega \textrm{Im}\left [ \chi\left ( \omega \right ) \right ]=\)

\(=\varepsilon _0\left | E_0 \right |^2\frac{nq^2}{2m}\frac{\gamma\omega^2}{\left ( \omega_{0}^{2}-\omega^2 \right )^2+\gamma^2\omega^2}>0\)

Este trabalho do campo sobre os dipolos resulta numa perda de energia de energia do campo e deve-se, evidentemente, à viscosidade do meio. Qual a origem desta viscosidade? A causa principal é a radiação emitida pela carga acelerada e esta perda de energia pode ser modelizada por um meio viscoso. Para \(\gamma\ll \omega_0\), há uma absorção ressonante de energia quando \(\omega\simeq \omega_0\). Note-se, finalmente, que \(\chi_e(0)=\frac{nq^2}{m\omega_{0}^{2}>0}\), pelo que \(\frac{\varepsilon }{\varepsilon _0}=1+\chi_e(0)>1\), uma propriedade genérica da permitividade estática.

Apêndice 2.

Um modelo para a susceptibilidade magnética.

O modelo de Lorentz também conduz a resultados simples para o comportamento do átomo sob ação de um campo magnético. Admita-se que o eletrão está submetido ao potencial harmónico com centro no núcleo: \(V\left ( \vec{r} \right )=\frac{1}{2}m\omega_{0}^{2}\left | \vec{r} \right |^2\). Ignorando qualquer efeito de viscosidade e considerando, de momento, apenas o movimento no plano \(xy\), as equações de movimento têm soluções bem conhecidas, sendo, aqui, útil escreve-las como sobreposição de dois movimentos circulares. Para isso, define-se \(\omega_\pm =x\pm iy\), com \(\omega_\pm \left ( t \right )=\omega_\pm \left ( 0 \right )e^{\pm i\omega_0t}\). Deste modo, \(w_±\) representa um movimento circular em sentido retrógrado e \(w_−\) um movimento circular em sentido directo (movimentos observados segundo o eixo \(z\)). Se, agora, se considerar a ação de um campo magnético \(B\) aplicado segundo \(z\), as equações de movimento ficam:

\(m\frac{d^2x}{dt^2}=-m\omega_{0}^{2}x-\left | q_e \right |B\frac{dy}{dt}\)

\(m\frac{d^2y}{dt^2}=-m\omega_{0}^{2}y+\left | q_e \right |B\frac{dx}{dt}\)

\(m\frac{d^2z}{dt^2}=-m\omega_{0}^{2}z\)

O movimento na direcção do campo não é modificado, apresentando uma oscilação com a frequência angular própria, \(\omega_0\). Quanto ao movimento no plano perpendicular ao campo, usem- -se as variáveis \(\omega_\pm \left ( t \right )\) para obter:

\(\frac{d^2\omega_\pm}{dt^2}+\omega_{0}^{2}\omega_\pm=i\omega_c\frac{d\omega_\pm}{dt}\)

onde \(\omega_c\equiv \frac{\left | q_e \right |B}{m}\omega_c\equiv \frac{\left | q_e \right |B}{m}\) é a frequência ciclotrónica. Procurando soluções da forma \(e^{i\omega t}\), obtém- se:

\(\omega_\pm\frac{\omega_c\pm\sqrt{\omega_{0}^{2}+4\omega_{0}^{2}}}{2}\)

Os dois movimentos circulares passam a ter frequências diferentes, com os seguintes limites:

• Para campos fracos \(\left ( \omega_c\ll \omega_0 \right )\): \(\omega_\pm\rightarrow \pm\omega_0+\frac{\omega_c}{2}\)
• Para campos fortes \(\left ( \omega_c\gg \omega_0 \right )\):

\(\omega_+\rightarrow \omega_c+\frac{\omega_{0}^{2}}{\omega_c}\; \; \; \; \; \; \; \; \; \; \; \omega_-\rightarrow -\frac{\omega_{0}^{2}}{\omega_c}\)

A carga elétrica \(-\left | q_e \right |\) num movimento circular de frequência angular \(\omega\) equivale a uma espira percorrida pela corrente de intensidade \(\left | q_e \right |\frac{\omega}{2\pi}\), originando um momento magnético \(\left | q_e \right |\frac{\omega}{2\pi}\pi R^2\), onde \(R\) é o raio da espira. Assim, àqueles dois movimentos circulares correspondem dois momentos magnéticos segundo o eixo \(z\), que, para campo fraco, são:

\(\mu_+=\left | q_e\left | \frac{1}{2} \right |w_+(0) \right |^2\left ( \omega_0+\frac{\omega_c}{2} \right )\)

\(\mu_-=-\left | q_e\left | \frac{1}{2} \right |w_-(0) \right |^2\left ( \omega_0-\frac{\omega_c}{2} \right )\)

Em campo nulo, \(\omega_\pm\) representam dois momentos magnéticos iguais e opostos. Quando o campo magnético aumenta, \(\omega_+\) apresenta uma resposta paramagnética (aumenta com o campo), enquanto \(\omega_-\) apresenta uma resposta diamagnética (diminui com o campo).

Uma carga acelerada emite radiação eletromagnética, sendo o respectivo campo elétrico perpendicular à aceleração e à direcção de observação. Deste modo, a radiação emitida por este oscilador será vista como três riscas (frequências \(\omega_\pm\) e (frequências \(\omega_0\), linearmente polarizadas, nas direcções perpendiculares ao campo, e duas riscas (frequências (frequências \(\omega_\pm\)) circularmente polarizadas, quando observadas na direcção do campo. Tal é a explicação do efeito Zeeman normal prevista por H. A. Lorentz em 1895 e observada por P. Zeeman, no ano seguinte, o que lhes valeria o prémio Nobel em 1902.

Referências

---

Criada em 20 de Dezembro de 2020
Revista em 12 de Fevereiro de 2021
Aceite pelo editor em 15 de Março de 2023