Números perfeitos
Referência : Santos, J. C., (2020) Números perfeitos, Rev. Ciência Elem., V8(4):056
Autor: José Carlos Santos
Editor: José Ferreira Gomes
DOI: [https://doi.org/10.24927/rce2020.056]

Resumo
Um número perfeito é um número natural que é igual à soma dos seus divisores (exceto ele próprio). O conceito de número perfeito é dos mais antigos da Matemática, mas ainda estamos longe de saber tudo sobre eles. Vamos ver a sua história desde a Antiga Grécia até aos nossos dias.
Antiguidade
O mais antigo texto onde os números perfeitos são mencionados é também um dos textos matemáticos mais famosos jamais escritos: os Elementos de Euclides, que datam aproximadamente de 300 a.C.. Aí, Euclides define um número perfeito como sendo um número natural cuja soma dos divisores próprios (isto é, os divisores diferentes do próprio número) seja igual ao número de que se partiu. O menor número perfeito é 6: a soma dos seus divisores próprios (1, 2 e 3) é 6. O exemplo seguinte é 28. Os divisores próprios de 28 são 1, 2, 4, 7 e 14 e a soma destes números é 28.
Na época de Euclides, só se conheciam mais dois números perfeitos: 496 e 8128. De facto, Euclides não menciona nenhum destes quatro números. Em vez disso, fornece uma receita para obter números perfeitos, que é a seguinte:
- toma-se um número natural \(n\);
- verifica-se se \(2^{n}-1\) é ou não um número primo;
- caso a resposta seja afirmativa, então \(\left ( 2^{n}-1 \right )\times 2^{n-1}\) é um número perfeito.
Testemos isto:
- Se \(n = 1\), então \(2^{n}-1 =1\), que não é primo.
- Se \(n = 2\), então \(2^{n}-1 =3\), que é primo. E \(\left ( 2^{2}-1 \right )\times2=6\), que é um número perfeito.
- Se \(n = 3\), então \(2^{n}-1 =7\), que é primo. E \(\left ( 2^{3}-1 \right )\times2^{2}=28\), que é um número perfeito.
- Se \(n = 4\), então \(2^{n}-1 =15\), que não é primo.
- Se \(n = 5\), então \(2^{n}-1 =31\), que é primo. E \(\left ( 2^{5}-1 \right )\times2^{4}=496\), que é um número perfeito.
- Se \(n = 6\), então \(2^{n}-1 =63\), que não é primo.
- Se \(n = 7\), então \(2^{n}-1 =127\), que é primo. E \(\left ( 2^{7}-1 \right )\times2^{6}=8128\), que é um número perfeito.
Até aqui, tudo funciona bem: o método de Euclides resulta e dá origem a todos os números perfeitos conhecidos na Antiguidade.
Antes de prosseguirmos, é interessante observar que, durante muito tempo, os números perfeitos eram considerados interessantes por causa da numerologia. Por exemplo, Fílon de Alexandria, um filósofo judeu do primeiro século da nossa era, afirmou que Deus fez o mundo em seis dias por seis ser um número perfeito, ideia essa que seria repetida por vários teólogos cristãos, incluindo Santo Agostinho. E Fílon também defendeu que os ciclos lunares são de vinte e oito dias por vinte e oito ser um número perfeito.
Euclides não foi o único matemático da Antiguidade a interessar-se pelos números perfeitos. Nicómaco de Gerasa, um contemporâneo de Fílon, estudou os números perfeitos e afirmou (sem demonstrar) que:
- O nésimo número perfeito tem n algarismos.
- O algarismo das unidades dos números perfeitos é 6 e 8 alternadamente (e, em particular todos os números perfeitos são pares).
- O método de Euclides não só fornece números perfeitos, como dá origem a todos os números perfeitos.
- Há uma quantidade infinita de números perfeitos.
Iremos ver qual é o ponto de vista atual relativamente a cada uma destas afirmações.
Idade Média
Uma pergunta natural a colocar é a de saber porque é que não se continuaram a obter novos números primos recorrendo ao processo descrito por Euclides. A resposta é simples: determinar se \(2^{n}-1\) é ou não primo leva a cálculos cada vez mais extensos à medida que n cresce. Já vimos que \(2^{n}-1\) é primo quando n é igual a 2, 3, 5 ou 7. Acontece que o próximo caso em que \(2^{n}-1\) é primo tem lugar quando \(n = 13\); tem-se então \(2^{13}-1=8191\), de onde resulta que \(33550336 \ (= 8191 \times 2^{12})\) é um número perfeito. Esta constatação deve-se a Ibn Fallus, um matemático persa do séc. XIII.
De facto, é preciso ler com alguma reserva aquilo que Ibn Fallus escreveu. Com efeito, parece que ele acreditava que, sempre que n é primo, o número \(2^{n}-1\) também é primo. Mas isto não é verdade: 11 e 23 são primos, mas \(2^{11}-1=23\times 89\) e \(2^{23}-1=47 \times 178481\). Por outro lado, é verdade que, como Ibn Fallus afirmou, \(2^{17}-1\) e \(2^{19}-1\) são primos, de onde resulta que 8 589 869 056 e 137 438 691 328 são número perfeitos.
Resulta daqui que as afirmações de Nicómaco de Gerasa relativamente a números perfeitos não podem ser todas verdadeiras. Com efeito:
- Se o método de Euclides der de facto origem a todos os números perfeitos, o quinto número perfeito é 33 550 336 que tem oito algarismos e não cinco. Não é verdade, então, que o n-ésimo número perfeito tenha n algarismos.
- Supondo ainda que o método de Euclides dá origem a todos os números perfeitos, também não é verdade que o algarismo das unidades dos números perfeitos seja 6 e 8 alternadamente; com efeito, o algarismo das unidades quer do quinto quer do sexto número perfeito é igual a 6.
Renascença
As contribuições de Ibn Fallus só se tornaram conhecidas na Europa séculos após o renascer do interesse neste tipo de assuntos. Em meados do século XV, Regiomontanus redescobriu o quinto número perfeito (33 550 336). Um século mais tarde, Hudalrichus Regius foi a primeira pessoa a aperceber-se de que, mesmo que n seja primo, não é necessariamente verdade que \(2^{n}-1\) seja primo; o exemplo que ele deu já foi visto atrás: \(2^{11}-1=23\times 89\).
Século XVII
No início do século XVII, o italiano Pietro Cataldi provou que, se n for composto, então \(2^{n}-1\) também é composto. Logo, só vale a pena testar se \(2^{n}-1\) é primo quando o próprio n for primo. Como já vimos, mesmo que n seja primo, é possível que \(2^{n}-1\) seja composto.
Cataldi foi mais cuidadoso do que Ibn Fallus e verificou, com imensos cálculos, que 219 – 1 é primo, confirmando assim que 137 438 691 328 é um número perfeito.
Algumas décadas depois, o francês Pierre de Fermat encontrou uma maneira de facilitar a tarefa de determinar se \(2^{n}-1\) é primo, quando \(n\) é primo. Com efeito, ele provou que todos os fatores primos de um tal número são da forma \(2 \times n \times m + 1\), para algum número natural m. Isto bate certo com o que foi visto atrás, pois:
- \(2^{11}-1=23\times 89\) e tanto 23 como 89 são da forma \(2 \times 11 \times m + 1\), com \(m = 1\) e \(m = 4\) respetivamente;
- \(2^{23}-1=47\times 179491\) e tanto 47 como 178 481 são da forma \(2 \times 23 \times m + 1\), com \(m = 1\) e \(m = 3880\) respetivamente.
A vantagem de se saber que todos os fatores primos são daquela forma tem origem, naturalmente, em haver muitos menos fatores primos a testar.
Um contemporâneo de Fermat, o também francês Marin Mersenne começou a fazer uma pesquisa sistemática dos números primos \(p\) para os quais \(2^{p}-1\) também é um número primo. Isto levou a que, hoje em dia, se designem por primos de Mersenne os números primos da forma \(2^{p}-1\).
Século XVIII
Em 1747, Leonhard Euler provou que qualquer número perfeito par pode ser obtido pelo método de Euclides (o que já tinha sido conjeturado por volta do ano 1000 pelo matemático persa Alhazen). Sendo assim, ficou definitivamente estabelecido que não é verdade que o algarismo das unidades dos números perfeitos é alternadamente 6 e 8. No entanto, é verdade que o algarismo das unidades de qualquer número perfeito par é necessariamente 6 ou 8. De facto, já Pietro Cataldi observara que o algarismo das unidades de um número perfeito obtido pelo método de Euclides só pode ser 6 ou 8. Visto que não há outros números perfeitos pares além destes, fica assim provado o resultado.
Uma consequência deste resultado de Euler é que a cada primo de Mersenne \(\left ( 2^{p}-1 \right )\) corresponde um número perfeito par (\(\left ( 2^{p}-1 \right )\times 2^{p}-1\)) e vice-versa. Ou seja, descobrir novos primos de Mersenne é o mesmo que descobrir novos números perfeitos pares.
O mesmo Euler foi a primeira pessoa na Europa a encontrar um novo número perfeito em quase dois séculos: já se sabia que o oitavo primo de Mersenne é \(2^{31}-1\); consequentemente, o oitavo número perfeito é \(\left ( 2^{31}-1 \right )\times 2^{30}=2305843008139952128\).
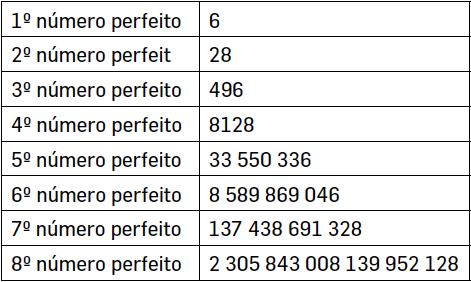
Vejamos quais eram os números perfeitos conhecidos até ao fim do século XVIII:
O que resta descobrir
Naturalmente, prosseguir por este caminho leva a cálculos cada vez mais complexos, mas não necessariamente a uma melhor compreensão do assunto. Vejamos sucintamente o que é que surgiu nesta área após a contribuição de Euler.
Em primeiro lugar, há o estudo dos primos de Mersenne. A contribuição de Fermat facilitou a tarefa de determinar se, dado um número primo, o número \(2^{p}-1\) é ou não primo. Mas, mesmo para números primos relativamente pequenos, isto pode dar origem a cálculos imensamente longos. Para lidar com este problema, for criado o teste de Lucas-Lehmer, na década de 1930. É um teste para determinar se um número da forma \(2^{p}-1\) é ou não primo. Continua a ser usado hoje em dia em cálculos feitos por computador (já há décadas que os maiores números primos conhecidos são demasiado grandes para que a sua primalidade possa ser confirmada por cálculos feitos à mão). O resultado de haver um teste de primalidade eficiente feito especificamente para estes números tem como consequência que já há quase trinta anos que, de cada vez que se descobre um novo número primo maior do que qualquer outro até então conhecido, esse número seja sempre um primo de Mersenne. O recordista atual, descoberto em dezembro de 2018, é 282 589 933 – 1.
Este número também é o 51º número de Mersenne a ser descoberto. Consequentemente, só se conhecem 51 números perfeitos pares (e, como será desenvolvido mais à frente, não se conhece nenhum número perfeito ímpar).
Um problema interessante é o de saber se há uma infinidade de números perfeitos (como defendia Nicómaco de Gerasa) ou, pelo contrário, se há somente um número finito deles. Como a cada número perfeito par corresponde um primo de Mersenne e vice-versa, afirmar que não se sabe se há uma infinidade de números perfeitos pares é o mesmo que afirmar que não se sabe se há uma infinidade de primos de Mersenne.
E o que é que se sabe sobre os números perfeitos ímpares? Muito pouco: nunca foi descoberto nenhum, mas também nunca foi provado que um tal número não existe. No entanto, sabe-se que se um tal número existir, então
- terá, no mínimo, 1500 algarismos;
- o seu maior fator primo é maior do que 10 000 000;
- tem, pelo menos, 10 fatores primos distintos.
Conclusão
Os números perfeitos são um exemplo (entre muitos outros) de um tópico matemático que, apesar de ser estudado desde a Antiguidade, continua a ser uma fonte de problemas para os matemáticos do século XXI.
Referências
- EUCLIDES Elementos, Traduzido por Irineu Bicudo. São Paulo: Editora Unesp, 2009.
- ROBERTSON et al. Perfect Numbers: MacTutor History of Mathematics Archive, Janeiro 2020.
Criada em 4 de Fevereiro de 2020
Revista em 9 de Setembro de 2020
Aceite pelo editor em 15 de Dezembro de 2020
