Modelo SIR em epidemiologia
Referência : Tavares, J, (2017) Modelo SIR em epidemiologia, Rev. Ciência Elem., V5(2):020
Autor: João Nuno Tavares
Editor: José Ferreira Gomes
DOI: http://doi.org/10.24927/rce2017.020

Resumo
Neste pequeno texto, procura-se ilustrar, através de um modelo simples (SIR), como a Matemática pode ser útil na previsão da evolução de uma epidemia e na tomada de decisão sobre estratégias de combate à sua propagação (vacinação, quarentenas, etc.).
1. introdução
1.1. Ao longo dos séculos, tem havido muitos exemplos de epidemias de várias doenças com efeitos dramáticos na população humana (e não só). Uma das mais conhecidas é a Peste Negra na Europa no século XIV[1], que dizimou entre 25 a 75 milhões de pessoas (cerca de um terço da populacão europeia da altura!). Nos tempos coloniais, a propagação de doenças europeias, tais como o sarampo e a varíola, teve um impacto desastroso sobre certas populacões indígenas que não tinham desenvolvido resistência a essas doenças.
Hoje em dia, existem ainda exemplos trágicos - a SIDA, o vírus Ébola, o ZIKA e muitos outros.
Se conseguirmos compreender como uma doença se
propaga numa determinada população, então estaremos melhor equipados
para a conter, através de vacinação ou quarentena.
1.2. Muitas doenças são propagadas por
indivíduos infectados que, por contacto com in- divíduos susceptíveis,
os contagiam. Estas incluem gripe, sarampo, varicela, febre glandular e
SIDA. Por outro lado, a malária é transmitida por meio de um hospedeiro,
um mosquito, que transporta a doença de indivíduo para indivíduo.
Algumas doenças são mais contagiosas do que outras. Sarampo e gripe são
altamente contagiosas, enquanto a febre glandular é muito menos. Muitas
doenças, tais como papeira e sarampo, conferem uma imunidade ao longo da
vida; no entanto, gripe e febre tifóide têm períodos curtos de imunidade
e podem ser contraídas mais do que uma vez.
1.3. Comecemos por esclarecer alguns conceitos prévios que surgem recorrentemente na modelação de epidemias.
- O período de incubação da doença é o tempo entre a infecção e a aparência visível de sintomas. Isto não deve ser confundido com o
- período de latência, que é o período de tempo entre a infecção e a capacidade de infectar alguém por contágio.
O período de latência é mais curto do que o período de incubação – um indivíduo pode estar a propagar a doença, sem ter até consciência de que a tem! Para o sarampo, o período de incubação é de cerca de 2 semanas e o período de latência é aproximadamente 1 semana.
Vamos neste Módulo aprender a modelar matematicamente a
dinâmica da propagação de uma doença (gripe, para sermos mais
concretos), adoptando algumas hipóteses simplificadoras (como aliás se
faz em qualquer modelo matemático) que serão enunciadas já de seguida.
2. hipóteses de modelação
2.1. Vamos modelar a dinâmica de uma doença infecciosa (gripe, por exemplo), que se propaga numa certa população (alunos de uma escola por exemplo).
Para isso, começamos por dividir a população em 3 grupos ou classes:
- S = {Susceptíveis} - os que podem apanhar gripe, mas que actualmente não estão infectados;
- I = {Infecciosos} - os que estão infectados com gripe e podem contagiá-la a outros;
- R = {Removidos} - os que não podem apanhar gripe, ou porque recuperaram perma- nentemente e ficaram imunes (pelo menos durante o período em análise), ou porque são naturalmente imunes ou porque morreram!
2.2. Por ser mais simples, vamos modelar a dinâmica da doença, isto é, a evolução temporal dos tamanhos de cada uma das classes acima referidas, usando tempo discreto:
\(t_{0}, t_{1}, t_{2}, t_{3}, ..., t_{n}, t_{n + 1}\)
O intervalo entre dois períodos consecutivos \(\Delta t = t_{n + 1} - t_{n}, n = 1, 2, 3, ...\) supõe-se constante – é medido numa unidade de tempo apropriada (hora, dia, semana, ano, etc., conforme o contexto).
Portanto
\(t_{n + 1} = t_{n} + \Delta t, n = 0, 1, 2, ...\)
2.3. Seja \( t \enspace \epsilon \) {\( t_{0}, t_{1}, t_{2}, t_{3}, ... \)} um qualquer dos instantes acima referidos, e representemos por \( S(t) \), \( I(t) \) e \( R(t) \) o número de indivíduos, no instante R, respectivamente. A modelação da forma como evoluem estes grupos, em interacção uns com os outros, conduzirá a um sistema acoplado de equações.
Matematicamente é mais conveniente manter o número total de indivíduos constante, e por isso contamos todos os indivíduos mortos em R. Assim, supomos que
\( S(t) + I(t) + R(t) \equiv N \enspace (constante) \enspace \enspace \enspace\) (2.1)
para todo o \( t \enspace \epsilon \) {\(
t_{0}, t_{1}, t_{2}, t_{3}, ... \)}. Em geral pomos \( t_{0} = 0 \).
2.4. As hipóteses do modelo são as seguintes:
- H1 A população em análise é muito numerosa o que permite ignorar efeitos aleatórios, devidos às diferenças entre os indivíduos e outros factores.
- H2 Também assumimos que, em qualquer momento, a população é homogeneamente misturada, isto é, supomos que os infecciosos (infectados e contagiosos) e susceptíveis estão sempre distribuídos aleatoriamente na área em que a população vive (não se consideram eventuais heterogeneidades espaciais).
- H3 A doenca é transmitida por proximidade ou contacto entre um infeccioso e um susceptível.
- H4 Um susceptível fica infectado logo após a transmissão, isto é, ignoramos o período de latência da doença, fixando-o igual a zero.
- H5 Os infectados eventualmente recuperam e, uma vez recuperados, ficam para sempre imunes (pelo menos durante o periodo em análise).
- H6 Ignoramos nascimentos, mortes ou efeitos migratórios.
2.5. Consideremos agora um intervalo de tempo \( \left[ t, \enspace t + \Delta t \right] \), onde \( t \enspace \epsilon \) {\(t_{0}, t_{1}, t_{2}, t_{3}, ... \)}, e representemos por

É claro que
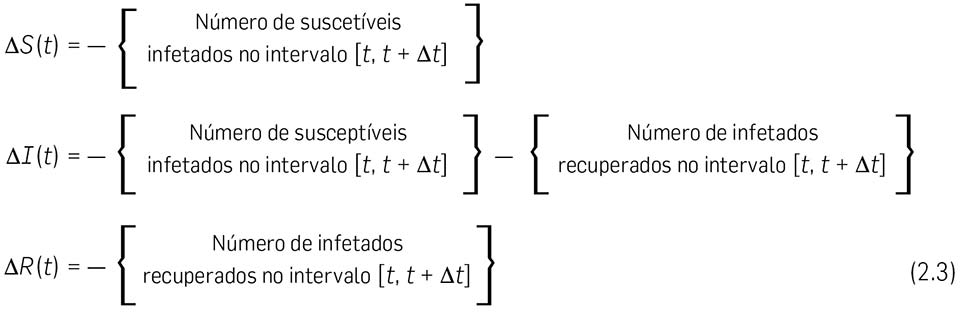
2.6 Vamos calcular em primeiro lugar o { Número de infetados recuperados no intervalo \( \left[ t, \enspace \Delta t \right] \) }. Este número não deve depender do número de indivíduos suscetíveis \( S(t) \), mas apenas do número de infetados \( I(t) \). No nosso modelo, assumimos que esse número (de infetados recuperados) é directamente proporcional ao número de infetados \( I(t) \) e também à duração do intervalo de tempo \( \Delta t \). Escrevemos pois
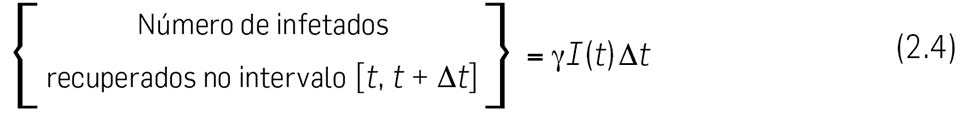
onde \( \gamma \) é uma constante positiva de
proporcionalidade, chamada taxa de recuperação ou
taxa de remoção. \( \gamma \) é uma taxa
per-capita e por unidade de tempo. O seu recíproco, \( 1/
\gamma \), pode ser identificado como o tempo de residência no
compartimento infeccioso, isto é, o tempo médio em que um indivíduo é
infecioso. Para a gripe, o período infecioso é tipicamente de 1 a 3
dias. Se o considerarmos igual a 2 dias, por exemplo, isto significa que
a taxa de recuperação é \( \gamma = 1/2 \) (por indivíduo e por dia) e
portanto num dia metade dos infetados recuperam – passam para o
compartimento R.
2.7. Vamos agora calcular { Número de suscetíveis infetados no intervalo \( \left[ t, \enspace \Delta t \right] \) }. Para modelar este número, podemos pensar da seguinte forma – é claro que o número de indivíduos infetados aumenta quando suscetíveis contraem a doença por contágio (que envolve algum tipo de contacto entre um suscetível e um infetado).
Suponhamos que cada indivduo contacta, por unidade de tempo, em média com \( c \) outros, escolhidos aleatoriamente. \( c \) diz-se a taxa de contacto per-capita e por unidade de tempo. Pela hipótese [H2] — população homogeneamente misturada — \( c \) é constante (uma hipótese muito questionavel!...).
A doença é transmitida apenas quando uma pessoa infeciosa contacta com um suscetível. Se a população total é constituída por \( N \) pessoas, a probabilidade de que alguém encontre um suscetível é igual a \( S(t)/N \), e portanto, uma pessoa infeciosa tem (em média) contacto com \( cS(t)/N \) susceptíveis, por unidade de tempo. Se \( p \) é a probabilidade de que um contacto resulte em contágio e, uma vez que existem \( I(t) \) indivíduos infetados no total, isso significa que o número de novas infeções, no intervalo de tempo \( \left[ t, \enspace \Delta t \right] \), é \( \left(cpS(t)I(t)/N \right) \Delta t \) e podemos escrever
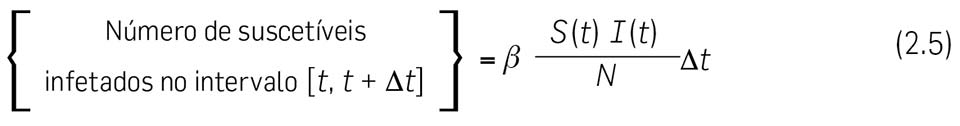
onde pusemos \( \beta = cp \). A constante \( \beta \) é chamada o coeficiente de transmissão e tem unidades tempo−1.
Reunindo todas estas informações, obtemos as equações seguintes para as variações do número de suscetíveis, infetados e recuperados no intervalo \( \left[ t, \enspace \Delta t \right] \)
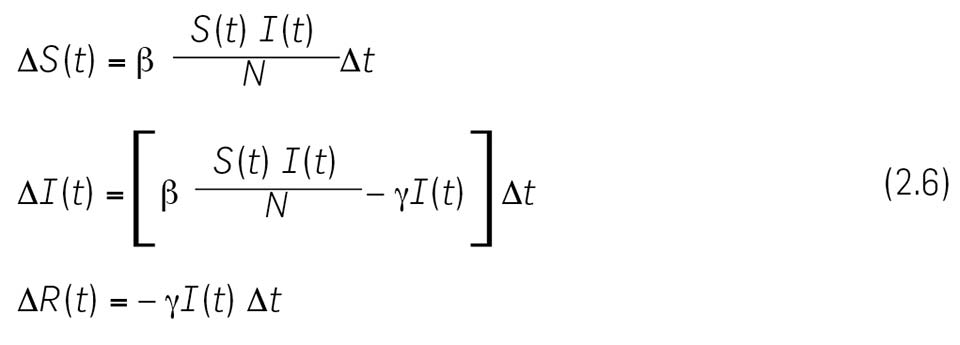
Esta discussão pode ser resumida e visualidada no diagrama de fluxo da Figura 1, cuja explicação deixamos à imaginação do leitor.
Um bom exercício é pensar como mudar as hipóteses simplicadoras noutras mais realistas e desenhar diagramas análogos ao da Figura 1 e, a partir deles, escrever equações análogas às equações SIR (2.6). Um exemplo possível é o da Figura 2 – qual a interpretação?
3. Um exemplo concreto
3.1. Na tabela seguinte mostra-se os números de infetados relativos a um surto de gripe numa escola com \( N = 763 \) alunos, durante 14 dias. O gráfico correspondente mostra-se na Figura 3
| Dia | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Infetados | 3 | 7 | 22 | 78 | 233 | 300 | 256 | 233 | 189 | 128 | 72 | 33 | 11 | 6 |
Na Figura 3 representam-se os gráficos de \( S(n) \), \( I(n) \) e \( R(n) \), obtidos através das equações SIR (2.6), com os valores seguintes para os parâmetros: \( \gamma = 0.44 \) e \( \beta = 1.68 \), correspondentes uma taxa de contacto \( c = 2 \) e a uma probabilidade de contágio \( p = 0.84 \). Como condições iniciais supomos que o surto começou com um único infeccioso em \( t_{0} = 0 \), de tal forma que \( I(0) = 1 \) e \( S(0) = 762 \). Examine detalhadamente o ficheiro Excel ModeloSIR gripe.xlsx. Mude os parâmetros com os cursores lá incluídos, e observe como mudam os gráficos.
Finalmente na Figura 5 comparam-se os dois gráficos – o de infectados, dados pela amostra, e o de infectados dados pelo modelo das equações SIR. Claro que o ajuste não é perfeito, mas é razoável!... As previsões do modelo parecem concordar bem com os dados da amostra. O número de infecciosos começa pequeno, aumenta substancialmente ao longo de 6 dias, e depois diminui gradualmente. Assim, nas últimas fases do surto, há uma possibilidade muito menor de um qualquer infeccioso entrar em contacto com alguém que ainda não foi infectado.
Resumindo: o que temos à partida é
- uma amostra, dada pela tabela acima referida, recolhida por observações directas reali- zadas ao longo de 14 dias, e
- um modelo – o das equações SIR, que deduzimos sob certas hipótese.
Talvez mudando estas hipóteses, que não são de forma alguma inquestionáveis, e portanto o modelo, obtivessemos um mais próximo dos dados reais da amostra.
Mas podemos talvez melhorar a situação, escolhendo de forma apropriada os parâmetros que temos ao dispôr – o coeficiente de transmissão \( \beta \) e a taxa de recuperação \( \gamma \). Existe um método de estimação destes parâmetros, muito usado nestas situações – o chamado método dos mínimos quadrados.
A ideia é escolher os parâmetros \( \beta \) e \( \gamma \) de tal forma que a função soma dos desvios quadráticos
\( \mathrm{F} \left( \gamma , \enspace \beta \right) = \sum_{n=10}^{4} \left[ I_{amostra} \left( n \right) - I_{modelo} \left( n \right) \right]^2 \enspace \enspace \enspace \) (3.1)
tenha o menor valor possível.
Veja a Figura 6 e o ficheiro Modelo SIR gripe EMQ.xlsx
4. Taxa de contacto e número de contacto
4.1. Os modelos de doenças infecciosas
são frequentemente formulados de uma maneira um pouco diferente da que
fizemos acima – em vez de números absolutos, como antes, usamos agora
proporções da população. Para grandes populações, em particular, esta é
uma abordagem natural, porque o tamanho exato da população pode não ser
conhecido.
4.2 Retomando o modelo SIR, vamos definir
\( s = \frac{S}{N} \), \( i = \frac{I}{N} \), \( r = \frac{R}{N} \enspace \enspace \enspace \) (4.1)
e reconstruir o modelo usando proporções. Observe agora que
\( s + i + r = 1 \)
porque estamos a medir frações da população. Vamos continuar a presumir que não há nascimentos ou imigração, de modo que o tamanho total da população \( N \) se mantem constante, apesar de \( N \) não aparecer nas nossas equações. Neste contexto, dividindo ambos os membros das equações (2.6) por \( N \) , obtemos as chamadas equações sir seguintes
\( \Delta s(t) = - \beta s (t) i(t) \Delta t \)
\( \Delta i(t) = \left[ \beta s (t) - \gamma \right] i(t) \Delta t \enspace \enspace \enspace \) (4.2)
\( \Delta r(t) = \gamma i(t) \Delta t \)
onde \( \beta \) é, como antes, o coeficiente de transmissão.
O valor de \( \beta \) depende é claro das
particularidades da doença sob estudo. Por exemplo, como a varicela é
altamente contagiosa, parece plausível que uma criança da escola
primária possa ter contato, suficiente para espalhar varicela, com
quatro outras crianças durante um dia. Neste caso, podemos tomar \(
\beta = 4 \) e \( \Delta t = 1 \) dia. Para uma doença menos contagiosa,
\( \beta \) pode ser um número tão pequeno como 0.02.
5. Valores limiar (threshold) e parâmetros críticos
5.1. Para analisar o modelo sir e ganhar alguma intuição biológica sobre os parâmetros do modelo, vamos usar as equações (4.2):
\( \Delta s(t) = - \beta s (t) i(t) \Delta t \)
\( \Delta i(t) = \left[ \beta s (t) - \gamma \right] i(t) \Delta t \enspace \enspace \enspace \) (5.1)
\( \Delta r(t) = \gamma i(t) \Delta t \)
Diremos que uma epidemia ocorre se \( \Delta i(t) > 0
\), para algum intervalo temporal \( \left[ t, \enspace t + \Delta t
\right] \) (isto é, se nesse período a proporção de infecciosos cresce).
Se \( \Delta i(t) ≤ 0 \) para todos os períodos, o tamanho da classe
infecciosa não aumenta e não existe qualquer foco da doença.
5.2. O primeiro passo para a compreensão da dinâmica da doença, é pois entender o sinal de \( \Delta i(t) \). Vejamos então como determinar se
\( \Delta i(t) = \left[ \beta s (t) - \gamma \right] i(t) \Delta t \enspace \enspace \enspace \) (5.2)
é positivo, negativo ou nulo.
É claro que se \( i(t) = 0 \) então \( \Delta i(t) = 0 \) - se não há infectados, não há doença. Suponhamos agora que \( i(t) > 0 \). Então \( \Delta i(t) \) será positivo, negativo ou nulo, se o mesmo acontece com \( \beta s(t) - \gamma \). Como \( \beta > 0 \), podemos concluir que
se \( s(t) > \gamma / \beta \), então \( \Delta i(t) > 0 \)
se \( s(t) = \gamma / \beta \), então \( \Delta i(t) = 0 \enspace \enspace \enspace \) (5.3)
se \( s(t) < \gamma / \beta \), então \( \Delta i(t) <
0 \)
5.3. Observe que, a partir de nossas fórmulas originais, temos sempre que \( \Delta s(t) ≤ 0 \), ∀\( t \) e, por isso, a proporção de susceptíveis nunca pode aumentar.
Isto significa que, se a proporção inicial de susceptíveis, \( s_{0} \), satisfaz
\( s_{0} < \frac{ \gamma }{ \beta } \)
então \( s(t) < \frac{ \gamma }{ \beta } \) e portanto, pela terceira implicação de (5.3), \( \Delta i(t) < 0 \) para todo \( t \), e a doença diminui – não há epidemia.
No entanto, quando a proporção inicial de susceptíveis, \( s_{0} \), satisfaz \( s(t) > \frac{ \gamma }{ \beta } \), o número de infecciosos cresce no primeiro período \( \left[ 0, \enspace \Delta t \right] \), isto é \( \Delta i(0) > 0 \), o que provoca uma epidemia.
Por este motivo, a razão \( \frac{ \gamma }{ \beta } \)
é um exemplo de um valor limiar ou crítico (threshold); a
relação de \( s_{0} \) com \( \frac{ \gamma }{ \beta } \) é um
determinante importante da dinâmica da doença. Como \( \frac{ \gamma }{
\beta } \) representa a taxa de remoção \( \gamma \) relativa ao
coeficiente de transmissão \( \beta \), chamamos-lhe a taxa de
remoção relativa.
6. O número básico de reprodução \( \Re_{o} \)
6.1. Uma abordagem ligeiramente diferente para o comportamento que descrevemos no ponto anterior, envolve reescrever a equação para \( \Delta i(t) \) na forma
\( \Delta i(t) = \gamma \left( \frac{ \beta }{ \gamma } s(t) - 1 \right) i(t) \Delta t \)
Uma análise semelhante do sinal de \( \Delta i(t) \), utilizando esta expressão, mostra que a pergunta \( \frac{ \beta }{ \gamma } \) agora é como a quantidade \( s_{0} \) se compara com 1. Os epidemiologistas chamam à expressão
\( \Re_{o} = \frac{ \beta }{ \gamma } s_{0} \enspace \enspace \enspace \) (6.1)
o número de reprodução básico da infecção.
Da discussão anterior concluímos que se \( \Re_{o} > 1
\), então \( \Delta i(0) > 0 \) e portanto ocorre uma epidemia.
6.2. Vamos considerar o número básico de reprodução
\( \Re_{o} = \frac{ \beta }{ \gamma } s_{0} = \left( \beta s_{0} \right) \frac{1}{ \gamma } \)
de um ponto de vista mais biológico, a fim de compreender o seu nome e importância conceptual.
Como vimos em (2.5), no modelo SIR o termo
\( \beta \frac{ S(0) I(0)}{N} \Delta t \)
mede o número de indivíduos infectados, no período inicial \( \left[ 0, \enspace \Delta t \right] \).
Em particular, pondo \( I(0) = 1 \) e \( s_{0} = S(0)/N \) , vemos que \( \beta s_{0} \Delta t \) é o número de susceptíveis infectados por contacto com um único infeccioso, no período inicial da epidemia. Daí que \( \Delta s_{0} \) é o número de susceptíveis infetados, por contacto com um único infeccioso, por unidade de tempo, no período inicial da epidemia.
Na verdade, se introduzirmos um infeccioso numa população de indivíduos todos susceptíveis ( \( S(0) = N − 1 \), \( I(0) = 1 \), \( R(0) = 0 \)), esse doente infeccioso pode, eventualmente, infectar muitos mais do que \( \beta s_{0} \) susceptíveis, uma vez que ele pode permanecer contagioso por muitos períodos de tempo. Por exemplo, suponhamos que uma criança permanece contagiosa com varicela durante 7 dias. Se usamos 1 dia como período (unidade tempo), a criança poderia infectar \( \beta s_{0} \times 7 \) susceptíveis ao longo de uma semana.
Por outro lado, se o período de contágio é de 7 dias, então em cada dia esperamos que aproximadamente 1/7 ou cerca de 14% do número total de infecciosos se mova da classe I para a classe R. Como a taxa de remoção γ mede a fracção da classe infecciosa “curada” durante um único período (1 dia, neste caso), vemos que uma boa estimativa para \( \gamma \) é \( \gamma \approx 1/7 \approx 0.1429 \).
Simultanemente, encontramos uma boa interpretação para \(1/ \gamma \) – é o tempo médio em que um indivíduo está infeccioso. Na prática, podemos estimar \(1/ \gamma \) em doenças reais, observando indivíduos infectados e determinando o tempo médio em que eles permanecem infecciosos.
Concluindo

6.3. Portanto \( \Re_{o} \) é interpretado como o número médio de infecções secundárias que seria produzido por um infeccioso numa população total de susceptíveis de tamanho \( S(0) \).
Note que o valor limiar \( \Re_{o} = 1 \) faz todo o
sentido do ponto de vista biológico. Se \( \Re_{o} > 1 \), então um caso
primário de doença gera mais do que um caso secundário da doença, o
tamanho da classe infecciosa aumenta, e o resultado é uma epidemia. Se
\( \Re_{o} = 1 \), então um indivíduo doente produz apenas um novo caso
da doença, e nenhuma epidemia pode ocorrer; não pode haver crescimento
do número de infecciosos. Quando \( \Re_{o} < 1 \), a doença morre. Em
suma, um epidemia ocorre se e somente se o número de reprodução básica
\( \Re_{o} > 1 \).
6.4. Como o número básico de reprodução tem uma interpretação tão significativa, os epi- demiologistas tentar achar uma expressão para \( \Re_{o} \) para qualquer modelo que eles propõem. Eis algumas estimativas típicas de \( \Re_{o} \) para algumas doenças infecciosas comuns (na era de pré-vacinação)
| Doença | \( \Re_{0} \) | |
| gripe | ≈ | 3-4 |
| sarampo | ≈ | 16-18 |
| varíola | ≈ | 4 |
| varicela | ≈ | 10-12 |
Veja o cálculo de \( \Re_{o} \) nas folhas Excel ModeloSIR gripe.xlsx e ModeloSIR gripe EMQ.xlsx.
Embora num modelo complicado, tal como doenças
sexualmente transmissíveis (HIV), podem incluir vários parâmetros
adicionais, uma combinação deles deve ser interpretável como um \(
\Re_{o} \) dessa doença. O número de reprodução básico \( \Re_{o} \)
desempenha um papel crucial em decisões de saúde pública, porque um
programa de prevenção da doença só será eficaz na prevenção de novos
surtos quando ele garante que \( \Re_{o} \leq 1\).
Exemplo
Suponhamos, para uma determinada doença, um doente infeccioso é introduzido numa população de 500 indivíduos susceptíveis. Vamos usar o modelo SIR, com período de tempo \( \Delta t = 1 \) dia (supondo que é adequado para descrever esta doença). Suponhamos, além disso, que os dados indicam que o coeficiente de transmissão é \( \beta = 0.5 \) e que o tempo médio de infecção é de 10 dias, após os quais o doente recupera (ou morre!). Portanto, neste caso, \( \gamma = 0.1 \) e
\( \Re_{o} = \frac{ \beta }{ \gamma } s_{0} \approx \frac{0.5}{0.1}1 = 5 \)
Como \( \Re_{o} = 5 > 1 \) espera-se uma epidemia. A
folha Excel mostra que o número de infectados tem um pico para \(n =
21\) ou 22 dias, aproximadamente igual a 250. Metade da população está
doente o que traduz uma epidemia severa, sem dúvida.
7. Estratégias de imunização. Vacinação
7.1. Uma população pode ser protegida da doença de várias maneiras. Por exemplo,
- o número de indivíduos susceptíveis podem ser reduzido através de vacinas,
- a taxa de contacto pode ser reduzida através de quarentenas ou campanhas de saúde pública, ou
- a taxa de remoção pode ser aumentada através de um melhor tratamento médico do doente.
Em suma, uma sociedade pode tentar mudar qualquer um
dos parâmetros ou condições iniciais do modelo que descreve a doença.
7.2 Vacinações, quando disponíveis,
são uma maneira atraente para controlar a dinâmica da doença, mas os
riscos privados e públicos de imunização deve ser equilibrado. Um dos
principais objetivos de qualquer programa de imunização é conseguir
imunidade global, (ou seja, garantir que nenhuma epidemia possa ocorrer,
mesmo se alguns casos da doença estão presentes). No entanto, existem
indivíduos que recebem vacinas mas têm algum pequeno risco de efeitos
secundários.
7.3. Como uma aplicação do número básico de reprodução \( \Re_{o} \), vamos considerar a vacinação de uma população. Admitindo que seria possível vacinar instantaneamente uma proporção \( P \) de uma população, que proporção P devemos vacinar para conseguir a erradicação da doença infecciosa?
A resposta é fácil utilizando o conceito de \( \Re_{o} \). Como \( \Re_{o} = s_{0} \), se vacinarmos uma proporção \( P \) da população de susceptíveis, então isto implica que o número básico de reprodução muda para
\( \Re_{o} = \frac{ \beta }{ \gamma } \left( 1 -P \right) s_{0} = \left( 1 - P \right) \Re_{o} \)
uma vez que a nova fracção de susceptíves é agora \( \left( 1 - P \right) s_{0} \).
Como devemos ter \( \Re_{o}^{vac} < 1 \) para erradicação, resolvendo em ordem a \( P \), obtemos a fórmula simples
\( P > 1 - \frac{1}{ \Re_{o} } \enspace \enspace \enspace\) (7.1)
Para a varíola, por exemplo, em que \( \Re_{o} \approx 4 \), calculamos \( P \approx 75% \) da população, mas para o sarampo, em comunidades não vacinadas, onde normalmente \( \Re_{o} \approx 15 \), então \( P \approx 93% \). Está claro deste cálculo porque é que, em todo o mundo, a varíola foi escolhida como alvo prioritário para a erradicação.
7.4. Estudo de imunização em doenças realistas requer o uso de modelos mais complicados. A dinâmica da doença, muitas vezes é diferente conforme a idade, estrato social, e outros factores, e, por isso, é usual dividir a população de susceptíveis, infecciosos e removidos em vários estratos ou subgrupos.
Um modelo pode dividir a população em vários subgrupos por idade, sexo ou outros fatores, e ser usado para determinar quais grupos devem ser alvo de uma campanha de imunização. Considerações sociais e médicas são cruciais.
Referências
Criada em 15 de Junho de 2017
Revista em 15 de Junho de 2017
Aceite pelo editor em 15 de Junho de 2017