Lei de Dalton
Referência : Lima, L.S., (2015) Lei de Dalton, Rev. Ciência Elem., V3(1):093
Autor: Luis Spencer Lima
Editor: Jorge Gonçalves
DOI: [http://doi.org/10.24927/rce2015.093]
A lei de Dalton, também conhecida como lei das pressões parciais, estabelece que a pressão total de uma mistura gasosa é igual à soma da pressão parcial de cada um dos gases que compõem a mistura. A lei de Dalton é estritamente válida para misturas de gases ideais, isto é, misturas de gases cujas partículas não se atraem nem se repelem e nas quais as colisões de cada um deles não são afectadas pela presença dos restantes. A pressão parcial de um gás numa mistura gasosa corresponde à pressão que este exerceria caso estivesse sozinho ocupando todo o recipiente, à mesma temperatura.
Este "princípio" foi estabelecido em 1801 pelo cientista inglês John Dalton (1766-1844), em estudos sobre a quantidade de vapor de água contida no ar a diferentes temperaturas.
Se se considerar uma mistura gasosa ideal de três componentes A, B e C, a pressão total (pt) é calculada da seguinte forma:

onde pA, pB e pC representam, respectivamente, as pressões parciais dos componentes gasosos A, B e C. A equação (1) é uma expressão matemática da Lei de Dalton.
Considere-se, agora, a aplicação da equação dos gases ideais a esta mistura que ocupa um determinado volume, V, a uma dada temperatura, T:
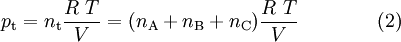
Nesta equação, nt representa o “número de moles” total de gás, que não é mais do que a soma da quantidade de substância ni de cada componente na mistura gasosa. Da mesma forma pode escrever-se a equação (2) para cada um dos componentes, dadas as condições de T e V serem as mesmas. Por exemplo, para o componente A:

Substituindo na equação (3) o factor constante RT/V pela igualdade traduzida pela equação (2), obtém-se:
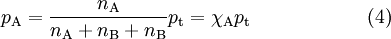
em que 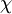 A representa a fracção molar do componente A.
A representa a fracção molar do componente A.
A equação (4) permite concluir é que se pode determinar a pressão parcial do componente A na mistura através da sua fracção molar.
O tratamento matemático traduzido pelas equações (3) e (4) é idêntico para os restantes componentes, pelo que se pode generalizar a equação (4) para um qualquer componente “i” de uma mistura gasosa ideal:

onde pi representa a pressão parcial do componente gasoso “i” e 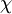 i a fracção molar desse mesmo componente na mistura gasosa. A equação (5) é outra forma matemática de expressar a Lei de Dalton.
i a fracção molar desse mesmo componente na mistura gasosa. A equação (5) é outra forma matemática de expressar a Lei de Dalton.
Como exemplo de cálculo, considere-se que se misturaram 0,20 mol de hélio (He), 0,50 mol de azoto (N) e 0,30 mol de oxigénio (O) num recipiente indeformável e isotérmico, e que a pressão total registada é de 3,10 bar (3,10 x 105Pa). Para se poder aplicar a lei de Dalton e calcular o valor da pressão parcial de cada componente na mistura gasosa, admite-se comportamento ideal para esta mistura de gases.
Com os dados fornecidos, é possível calcular a quantidade total de substância (“número de moles”) de gás: nt = 1,00 mol. Com base neste valor e na quantidade de cada componente, podem-se calcular as correspondentes fracções molares (= n/nt):

Atendendo à equação (5), consegue-se calcular o valor de cada uma das pressões parciais
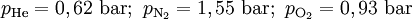
Como forma de confirmar os resultados obtidos, utiliza-se a equação (1) e verifica-se se a soma destes valores é igual ao valor da pressão total do sistema: 0,62 + 1,55 + 0,93 = 3,10 bar = pt.
Criada em 10 de Janeiro de 2011
Revista em 22 de Fevereiro de 2011
Aceite pelo editor em 25 de Fevereiro de 2011
