Imagens elétricas e o método de separação de variáveis
Referência : Lage, E., (2022) Imagens elétricas e o método de separação de variáveis, Rev. Ciência Elem., V10(1):003
Autor: Eduardo Lage
Editor: João Nuno Tavares
DOI: [https://doi.org/10.24927/rce2022.003]

Resumo
Nos condutores em equilíbrio eletrostático, o campo elétrico é nulo no seu interior — todo o espaço ocupado por um condutor está ao mesmo potencial; as cargas que esses condutores possuam distribuem-se unicamente pela sua superfície de modo, em geral, não uniforme e desconhecido. A determinação do campo de potencial elétrico fica, assim, reduzida ao seu conhecimento no espaço livre, seja entre condutores seja nas regiões ocas dos condutores, um problema típico de fenómenos de influência elétrica. Mas o facto de essa solução ser única, o que é aqui demonstrado, justifica a utilização do método das imagens elétricas onde se recorre a um problema já resolvido para encontrar a solução de outro problema de eletrostática. O método da separação de variáveis tem inúmeras aplicações em Física, sendo aqui apresentado como forma de encontrar a solução para alguns exemplos de interesse.
Um condutor é uma substância (cobre, alumínio, aço) onde se manifesta uma corrente elétrica se for aplicado um campo elétrico. Assim, num condutor em equilíbrio eletrostático, i.e., sem correntes, o campo elétrico deve ser nulo no seu interior: todo o espaço ocupado pelo condutor está ao mesmo potencial elétrico. Se o condutor tiver sido carregado eletricamente, todas as cargas localizar-se-ão na sua superfície de modo não uniforme, em geral. A determinação do campo elétrico fica reduzida às regiões não ocupadas pelos condutores (espaço vazio livre). Este problema eletrostático pode, então, ser formulado como segue, aqui ilustrado para dois condutores (FIGURA 1), embora se perceba a sua generalidade.

a) O potencial elétrico deve satisfazer a equação de Poisson no espaço livre[1]:
\(\Delta \varphi =-\frac{\rho }{\varepsilon _{0}}\) (1)
Aqui, a densidade de carga (representada por manchas vermelhas na FIGURA 1) é suposta conhecida e pode localizar-se na região exterior aos condutores ou nas suas partes ocas (exemplificado pelo condutor A na figura) ou mesmo ser nula.
b) Num qualquer condutor é dado o seu potencial elétrico, \(V_1\):
\(\varphi =V_1\) no Condutor A (2)
ou é dada a sua carga total, \(Q_2\):
\(\frac{Q_2}{\varepsilon _0}=\int_{\Sigma _{B}}^{}dS\vec{n}\cdot \vec{E}=-\int_{\Sigma _{B}}^{}dS\vec{n}\cdot \bigtriangledown \varphi \) no condutor B (3)
onde \(\vec{n}\) é a normal unitária à superfície do condutor e apontando para o espaço livre
Deve, aqui, notar-se que em nenhum condutor são dadas simultaneamente estas duas condições.
O caso particular \(\rho =0\) descreve os fenómenos de influência elétrica: as cargas nos condutores distribuem-se para garantir que os potenciais sejam constantes em cada condutor, embora essa distribuição seja a priori desconhecida. Dada a linearidade das equações de campo, segue-se que cargas e potenciais obedecem à equação genérica:
\(Q_i=\Sigma _{j}C_{ij}V_j\) (\(i\), \(j\) condutores) (4)
Os coeficientes de proporcionalidade \(C_{ij}\) são designados por capacidades parciais e, em particular, os elementos diagonais são as capacidades dos respetivos condutores tomados isoladamente (i.e., \(C_{11}\) é a capacidade do condutor 1), recordando-se, como exemplos, as capacidades de condutores cilíndricos ou esféricos obtidas noutro artigo[2].
Um importante resultado para o problema eletrostático atrás enunciado, é a unicidade de solução da equação (1) sujeita às condições fronteira equações (2) e (3).
A unicidade de solução traduz-se na afirmação, aparentemente trivial, que se for encontrada uma solução para o problema eletrostático, então essa é a solução. É esta afirmação que fundamenta o método das imagens elétricas que agora se expõe através de alguns exemplos ilustrativos.
Imagens elétricas
Consideram-se, a seguir, vários exemplos.
1.º Imagine-se uma carga pontual \(Q\) situada a uma distância \(d\) de um condutor plano ligado à terra (i.e., ao potencial nulo), tal como representado na FIGURA 2.
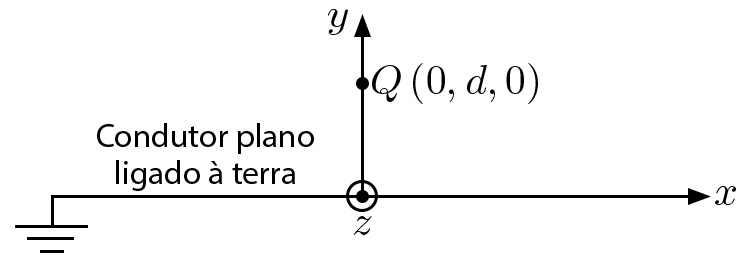
É evidente que \(\varphi =0\) abaixo do plano; acima do plano e no plano \(\left ( y\geq 0 \right )\) deve satisfazer as seguintes condições:
\(\Delta\varphi =-\frac{\rho_1}{\varepsilon _0}\)
\(\varphi =0\) em \(y=0\) (5)
Aqui, \(\rho_1\) representa a densidade para a carga pontual \(Q\) em \(y = d\), não sendo necessário especificar a sua forma analítica.
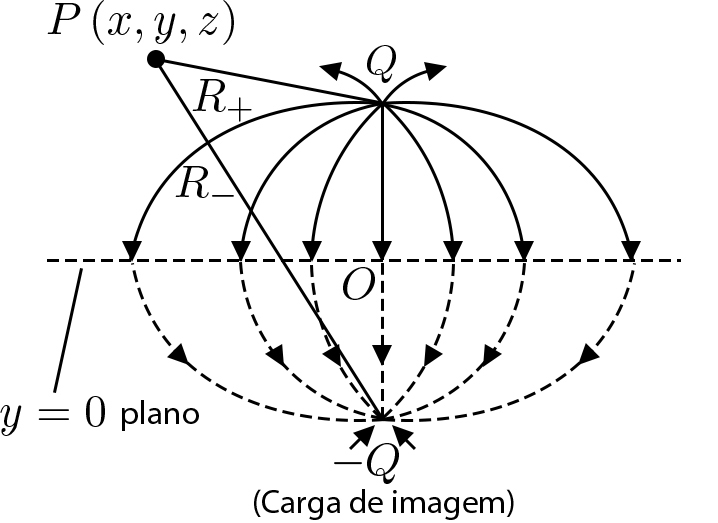
Considere-se, agora, um outro problema (FIGURA 3): duas cargas pontuais \(±Q\), separadas por uma distância \(2d\). É óbvio que é \(\varphi =0\) no plano equidistante das duas cargas, perpendicular à linha que as une. O campo de potencial gerado por estas duas cargas acima do plano satisfaz às mesmas condições da equação (5) do problema anterior. Então, o potencial acima do plano na FIGURA 3 é o potencial acima do plano condutor na FIGURA 2:
\(\varphi \left ( x,y,z \right )=\frac{Q}{4\pi _{0}}\left [ \frac{1}{\sqrt{x^{2}+\left ( y-d \right )^{2}+z^{2}}}-\frac{1}{\sqrt{x^{2}\left ( y+d \right )^{2}z^{2}}} \right ]\)
Note-se que este potencial é válido em todo o espaço para a FIGURA 3, mas só é solução do problema inicial (FIGURA 2) para \(y\geq 0\) que é a região de interesse. Tendo isto presente, facilmente se calcula o campo elétrico acima do plano condutor:
\(\vec{E}\left ( x,y,z \right )=\frac{Q}{4\pi\varepsilon _0}\left [ \frac{\left ( x,y-d,z \right )}{\left ( x^{2}\left ( y-d \right )^{2}+z^{2} \right )^{\frac{3}{2}}}-\frac{\left ( x,y+d,z \right )}{\left ( x^{2}+\left ( y+d \right )^{2}+z^{2} \right )^{\frac{3}{2}}} \right ]\)
Em particular, no condutor plano \(\left ( y=0 \right )\), obtém-se:
\(E_y\left ( x,0,z \right )=-\frac{Q}{4\pi\varepsilon _{0}}\frac{2d}{\left ( x^{2}+d^{2}+z^{2} \right )^{\frac{3}{2}}}\)
Donde se deduz (teorema de Gauss) a densidade de carga no condutor plano induzida pela presença da carga \(Q\):
\(\rho _s=-\frac{Q}{4\pi}\frac{2d}{\left ( x^{2}+d^{2}+z^{2} \right )^{\frac{3}{2}}}\)
A carga total induzida pode ser obtida integrando esta expressão sobre o plano; mas é mais fácil usar a FIGURA 3: o fluxo de \(\varepsilon _{0}E_y\left ( x,0,z \right )\) ao longo do plano condutor é igual ao seu fluxo através do plano que bissecta as cargas na FIGURA 3, sendo, pois, igual à carga abaixo desse plano, pelo que a carga total induzida no plano condutor é \(−Q\).
Qual a força que se exerce sobre a carga \(Q\) na FIGURA 2? Ela é devida ao campo elétrico gerado pelas cargas superficiais no plano condutor da FIGURA 2; mas este campo é o mesmo que tem origem na carga \(−Q\) da FIGURA 3. Assim, a força pretendida é:
\(F_y=-\frac{Q^{2}}{4\pi \varepsilon _0}\frac{1}{\left ( 2d \right )^{2}}\)
A força é atrativa, uma conclusão genérica para este tipo de problemas, e que é bem conhecido quando, num dia quente e seco, podemos observar a pequena faísca entre um dedo e a porta de um automóvel.
Por sobreposição, diversas outras questões podem ser facilmente resolvidas através do método das imagens. Por exemplo, se se considerar um dipolo elétrico2 em frente a um plano condutor ligado à terra, o campo de potencial acima deste plano é o mesmo que o gerado pelo dipolo e pela sua imagem elétrica (FIGURA 4).
A superfície da Terra é um fraco condutor e pode ser considerada ao potencial nulo. Numa trovoada, a nuvem apresenta uma separação de cargas elétricas formando um gigantesco dipolo. A nuvem e a sua imagem elétrica originam o campo elétrico no espaço entre a nuvem e o solo. Quando este campo excede um valor crítico, o ar deixa de ser um isolador, dando-se a descarga elétrica entre a nuvem e o solo.
Um outro interessante exemplo é exibido na FIGURA 5A): uma carga pontual nas proximidades de dois semiplanos condutores ortogonais ligados à terra.
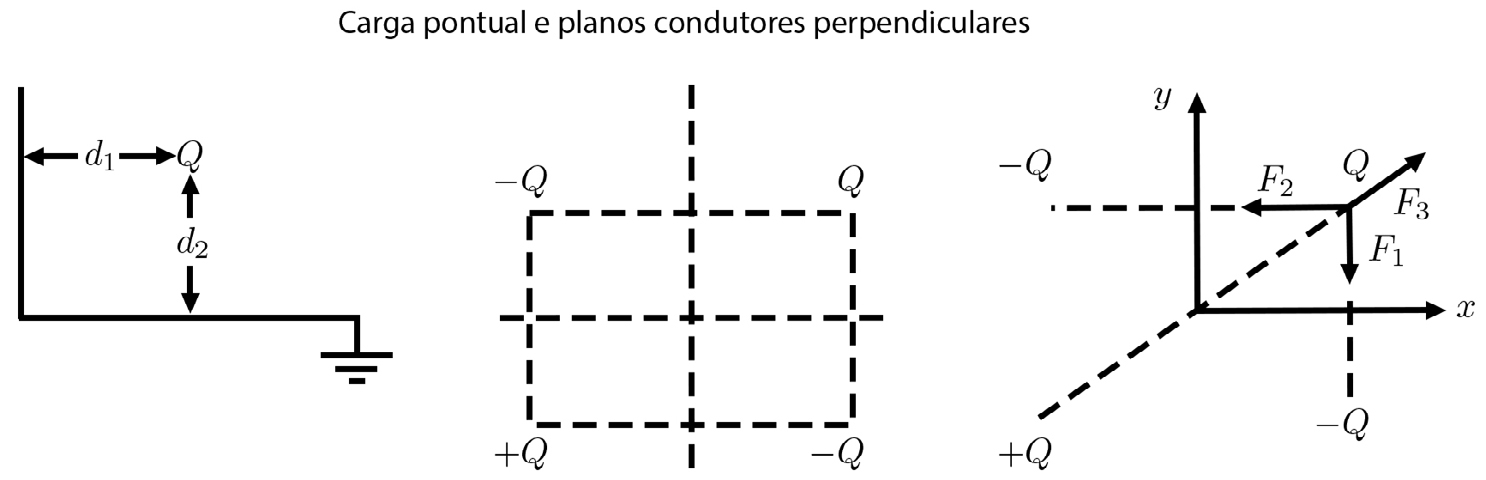
O campo elétrico na região de interesse (i.e., no primeiro “quadrante” da FIGURA 5A)) é o mesmo que o gerado pela carga e pelas suas três imagens elétricas (FIGURA 5B)), o que permite facilmente calcular a força que se exerce sobre a carga dada (FIGURA 5C)).
A FIGURA 6 exibe um eletroscópio, um dispositivo que passou a fazer parte dos museus de Ciência. Aproximando-se, sem tocar, um bastão eletricamente carregado da mesa do eletroscópio, é induzida uma distribuição de cargas na parte metálica do eletroscópio e que se manifesta na repulsão das lâminas de ouro.

Considere-se uma carga pontual \(Q\) no exterior de uma esfera (raio \(R\)) condutora, ligada à terra, à distância \(R + a\) do seu centro (FIGURA 7). É óbvio que o potencial dentro da esfera é nulo, interessando, pois, determiná-lo apenas no exterior.
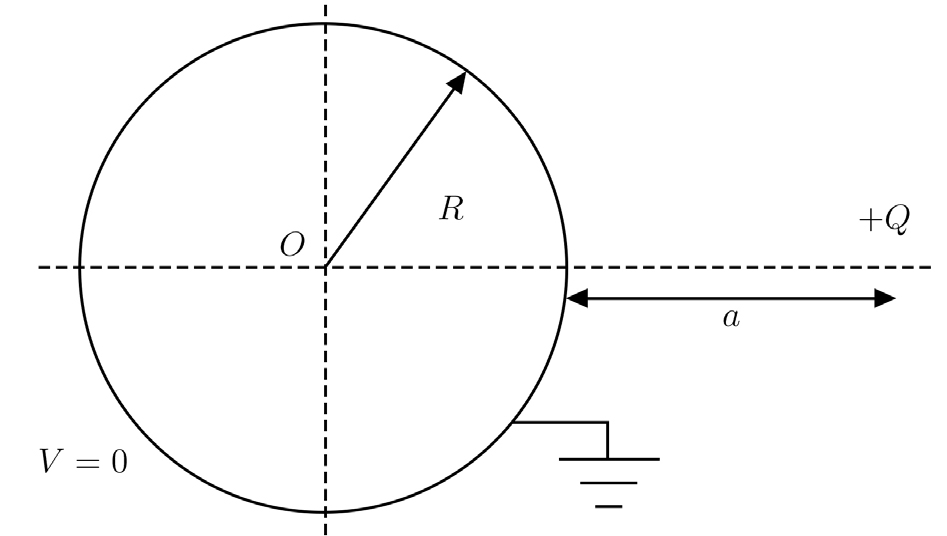
Atente-se, agora, na FIGURA 8 onde se representa a carga \(Q\) à distância \(R + a\) de uma origem \(O\) arbitrária, e uma carga \(Q′\) à distância \(R − b\) dessa origem, estando esta e as duas cargas colineares, tomando-se a reta que as une para eixo \(z\).
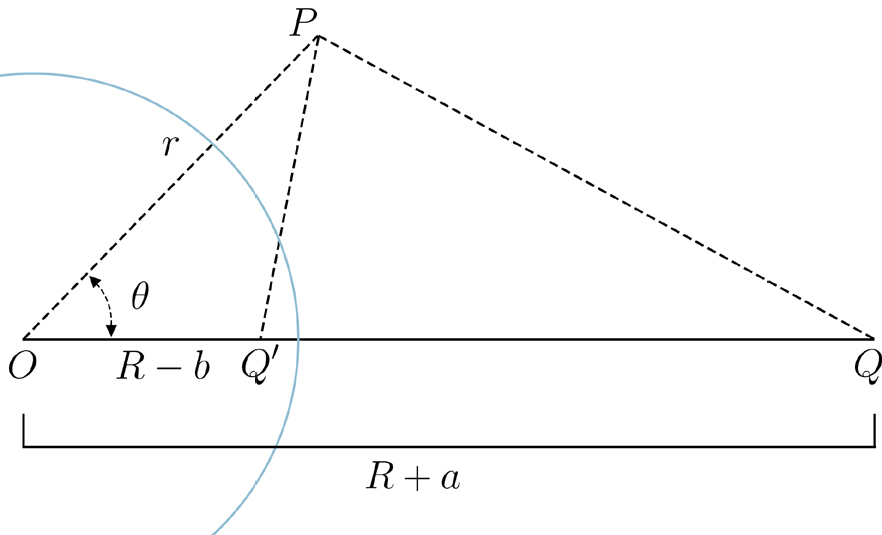
Usando coordenadas esféricas[3] para representar qualquer ponto \(P\) do espaço (à distância \(r\) da origem e formando \(OP\) um ângulo \(\theta\) com o eixo \(z\)), é fácil obter o potencial elétrico criado pelas duas cargas no ponto considerado:
\(\varphi \left ( r,\theta \right )=\frac{1}{4\pi\varepsilon _{0}}\left [ \frac{Q}{\sqrt{\left ( r\sin \theta \right )^{2}+\left ( r\cos\theta-R-a \right )^{2}}}+\frac{Q'}{\sqrt{\left ( r\sin\theta \right )^{2}+\left ( r\cos\theta -R+b \right )^{2}}} \right ]\) (6)
Escolhendo convenientemente \(Q′\) e \(b\), obtém-se potencial nulo numa esfera centrada na origem e de raio \(R\) ( a azul na FIGURA 8). Com efeito, tem-se:
\(4\pi\varepsilon _{0}\varphi \left ( R,\theta \right )=\frac{Q}{\sqrt{\left ( R\sin\theta \right )^{2}+\left ( R\cos\theta-R-a \right )^{2}}}+\frac{Q'}{\sqrt{\left ( R\sin\theta \right )^{2}+\left ( R\cos\theta-R+b \right )^{2}}}=\frac{Q/R}{\sqrt{1-2\frac{R+a}{R}\cos\theta+\left ( \frac{R+a}{R} \right )^{2}}}+\frac{Q'/\left ( R-b \right )}{\sqrt{1-2\frac{R}{R-b}\cos\theta+\left ( \frac{R}{R-b} \right )^{2}}}\)
que se anula para qualquer \(\theta\), i.e., em todos os pontos de uma esfera, se:
\(\frac{R+a}{R}=\frac{R}{R-b}\; \; \; \Leftrightarrow \; \; \; \frac{1}{b}=\frac{1}{a}+\frac{1}{R}\) (7)
\(\frac{Q'}{R-b}=-\frac{Q}{R}\; \; \; \Leftrightarrow \; \; \; Q'=-Q\frac{b}{a}\) (8)
Deste modo, a equação (6) representa o campo de potencial no exterior da esfera no problema original. O leitor reconhecerá a equação (7) como a equação dos focos conjugados de um espelho esférico, justificando a designação de \(Q′\) como carga imagem da carga \(Q\).
A partir da equação (6) pode ser obtido o campo elétrico e deduzir a densidade de carga na superfície da esfera (FIGURA 9).
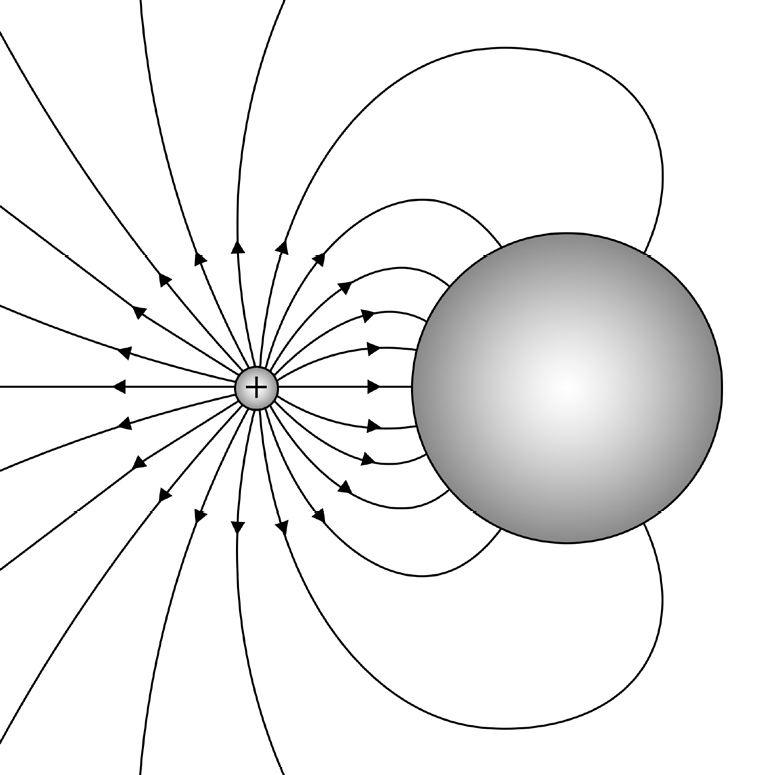
Mas se se pretender a carga total induzida na esfera, basta notar que o fluxo do campo elétrico na superfície esférica é o mesmo que na esfera-imagem (FIGURA 8): a carga total induzida na esfera condutora é \(Q'=-Q\frac{b}{a}\). O campo gerado pela carga distribuída na superfície esférica determina a força que se exerce na carga \(Q\) — mas este campo é, no exterior da esfera, o que é gerado pela carga imagem \(Q′\): a força sobre a carga \(Q\) é, simplesmente,
\(F_z=\frac{1}{4\pi\varepsilon _{0}}\frac{QQ'}{\left ( a+b \right )^{2}}=-\frac{1}{4\pi\varepsilon _{0}}\frac{Q^{2}\frac{b}{a}}{\left ( a+b \right )^{2}}\)
É interessante observar que a imagem de um dipolo elétrico2 é, em geral, um dipolo e uma carga elétrica. Tal resulta porque a imagem de uma carga depende de fatores geométricos relacionados com a sua posição.
Que acontece se a esfera condutora estiver a um potencial \(V\neq 0\)? Basta aplicar o princípio da sobreposição: à esfera deve acrescentar-se uma carga \(4\pi\varepsilon _0 VR\), distribuída uniformemente na sua superfície; deste modo, a carga total na esfera é \(Q'+4\pi\varepsilon _0 VR\), o potencial no seu interior é \(V\) e, no exterior, deve adicionar-se à solução anterior o potencial \(V\frac{R}{r}\).
A solução do problema exterior da esfera condutora, tal como atrás descrito, permite resolver o problema interior sem efetuar qualquer cálculo. Este problema interior consiste em determinar o campo de potencial dentro de uma superfície esférica ligada à terra e onde se encontra uma carga \(Q′\). Fora da esfera, o potencial é nulo; dentro da esfera, o potencial é originado pela carga \(Q′\) e pela carga \(Q\) que, agora, funciona como imagem da primeira. Dado ser nulo o campo elétrico fora da superfície esférica, o teorema de Gauss informa ser nula a carga total dentro da superfície e distribuída na superfície, pelo que a carga total na superfície é, simplesmente, \(−Q′\). A força que se exerce sobre \(Q′\) é, evidentemente, simétrica da força \(F_z\) atrás obtida.
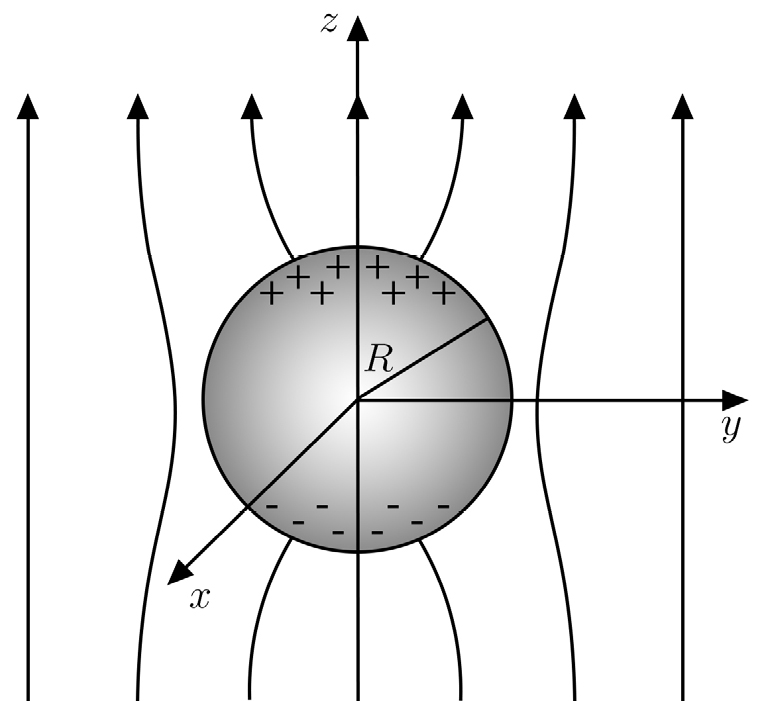
Regressando ao problema exterior, admita-se ser \(Q <\) \(0\) e considere-se a \(a\rightarrow \infty \) e \(Q\rightarrow -\infty \) mantendo \(\frac{Q}{4\pi\varepsilon _{0}}\frac{1}{\left ( a+R \right )^{2}}\equiv -E=\) constante . Tais limites significam que se está a considerar a esfera condutora mergulhada num campo elétrico E uniforme, com a direção e sentido do eixo \(z\). Usando a equação (7), vê-se que \(R-b\simeq \frac{R^{2}}{a}\rightarrow 0\) e, pela equação (8), \(Q'\simeq -Q\frac{R}{a}\rightarrow \infty \) mas \(Q'\left ( R-b \right )\simeq -Q\frac{R^{3}}{a^{2}}\rightarrow 4\pi\varepsilon _{0}R^{3}E\). Tendo em atenção estes resultados, a equação (6) tende, no limite referido e ignorando termos constantes, para a seguinte forma:
\(\varphi \left ( r,\theta \right )=E\left ( \frac{R^{3}}{r^{2}}-r \right )\cos\theta\) (9)
É, então, este o campo de potencial no exterior de uma esfera condutora submetida a um campo elétrico uniforme (FIGURA 10).
Notar-se-á que, na equação acima, o termo \(-Er\cos\theta=-Ez\) é o potencial do campo aplicado pelo que o outro termo é o potencial gerado pela distribuição de cargas na superfície da esfera. O campo elétrico, no exterior da esfera, é:
\(\vec{E}\left ( r,\theta \right )=-\bigtriangledown \varphi =E\vec{e}_z+2E\frac{R^{3}}{r^{3}}\cos\theta \vec{e}_r+E\frac{R^{3}}{r^{3}}\sin\theta\vec{e}_\theta\)
Reconhece-se que os dois últimos termos representam o campo de um dipolo elétrico. Na superfície da esfera \((r = R)\) é imediato verificar que \(E_\theta =0\), como devia ser, e que \(E_r\left ( R,\theta \right )=3E\cos\theta\). Assim, a carga distribui-se na superfície da esfera com a densidade:
\(\frac{\rho _{s}}{\varepsilon _{0}}=3E\cos\theta\)
Embora todos os exemplos apresentados façam, apenas, intervir uma carga pontual, é importante sublinhar que a solução está encontrada para qualquer distribuição dada de cargas, obtendo-se o campo de potencial por sobreposição dos campos originados pelas cargas elementares que constituem aquela distribuição.
Separação de variáveis
Este último problema serve, também, para ilustrar o método de separação de variáveis cuja aplicabilidade se estende a todos os tópicos da Física. O problema consiste em determinar o campo de potencial \(\varphi \left ( \vec{r} \right )\) no exterior da esfera e que satisfaz as seguintes condições:
\(\Delta\varphi =0\; \; \; \; \; r>R\)
\(\varphi =0\; \; \; \; \; r=R\)
\(\varphi \rightarrow -Er\cos\theta\; \; \; \; \; r\rightarrow \infty \)
Aqui, o centro da esfera é tomado como origem do referencial e o eixo \(z\) coincide em direção e sentido com o campo \(E\) aplicado (\(\theta\) é o ângulo que o vector de posição de qualquer ponto faz com o eixo \(z\)). A simetria do problema sugere que se usem coordenadas esféricas[4] e, também, que o potencial não deve depender de , o ângulo de rotação em torno do eixo \(z\). Assim:
\(\Delta\varphi =\frac{1}{r^{2}}\frac{\partial }{\partial r}\left ( r^{2}\frac{\partial \varphi }{\partial r} \right )+\frac{1}{\sin\theta}\frac{\partial }{\partial \theta}\left ( \sin\theta\frac{\partial \varphi }{\partial \theta} \right )=0\)
A condição limite sugere que se procurem soluções da forma \(\varphi \left ( r,\theta \right )=f\left ( r \right )\cos\theta\), devendo verificar-se \(f\left ( r \right )\underset{r\rightarrow \infty }{\rightarrow}-Er\). Substituindo na equação anterior, obtém-se:
\(\frac{1}{r^{2}}\frac{d}{dr}\left ( r^{2}\frac{df }{dr} \right )-\frac{2}{r^{2}}f=0\)
com as soluções independentes:
\(f\left ( r \right )=-Er+\frac{A}{r^{2}}\)
sendo \(A\) uma constante que se determina pela outra condição fronteira:
\(\varphi \left ( R,\theta \right )=0\; \; \; \rightarrow \; \; \; f\left ( R \right )=0\; \; \; \rightarrow \; \; \; A=ER^{3}\)
Deste modo, o campo de potencial é:
\(\varphi \left ( R,\theta \right )=Er\cos\theta+\frac{ER^{3}}{r^{2}}\cos\theta\)
como se havia encontrado.
Um outro exemplo é mostrado na FIGURA 11.
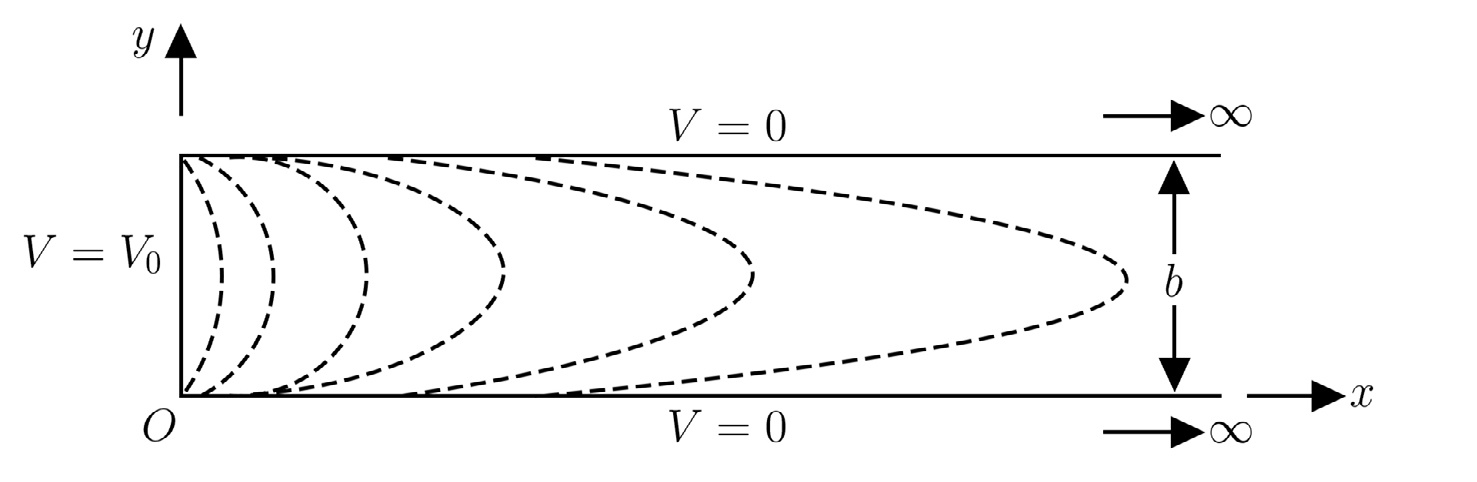
Uma calha é constituída por dois planos condutores paralelos e ligados à terra, isolados da base mantida ao potencial \(V_0\). Assim, com o sistema de eixos indicado, o campo de potencial deve satisfazer às seguintes condições:
\(\Delta\varphi =0\; \; \; \; \; 0<\)\(x;0<\)\(y<\)\(b\)
\(\varphi \left ( x,0 \right )=\varphi \left ( x,b \right )=0\; \; \; \; \; 0<\)\(x\)
\(\varphi \left ( 0,y \right )=V_0\; \; \; \; \; 0<\)\(y<\)\(b\)
Procurem-se soluções da forma \(\varphi \left ( x,y \right )=X\left ( x \right )Y\left ( y \right )\), onde \(X\) e \(Y\) são funções de uma única variável. Substituindo na equação de Laplace e rearranjando termos, tem-se:
\(\frac{X"}{X}+\frac{Y"}{Y}=0\)
onde a dupla plica indica 2.ª derivada em ordem ao argumento. Ora esta equação tem de ser satisfeita em todos os pontos no interior da calha. Mas, no primeiro membro, o primeiro termo só depende de \(x\) e o segundo termo só depende de \(y\). Então, cada um dos termos tem de ser uma constante, donde resulta:
\(\frac{X"}{X}=\alpha ^{2}\rightarrow X"=\alpha ^{2}X\)
\(\frac{Y"}{Y}=-\alpha ^{2}\rightarrow Y"=-\alpha ^{2}Y\)
Aqui, designou-se por \(\alpha ^{2}\) a constante de separação. Considerando a equação para \(Y\) (é a equação de “movimento” de um oscilador harmónico!), vê-se que \(Y (y)\) é da forma:
\(Y\left ( y \right )=A\sin\left ( \alpha y \right )+B\cos\left ( \alpha y \right )\)
Ora, atendendo à 1.ª condição fronteira, tem de ser \(Y (0) = Y (b) = 0\); então é \(B = 0\) e \(\sin (\alpha b) = 0\), pelo que \(\alpha b = n\pi\), com \(n\) inteiro positivo. Assim, \(Y\left ( y \right )\propto \sin\left ( n\pi\frac{y}{b} \right )\).
Considerando, agora, a equação para \(X (x)\), facilmente se conclui que esta função é combinação linear de \(e^{\alpha x}\) e \(e^{-\alpha x}\), mas a 1.ª função diverge para \(x\rightarrow +\infty \), pelo que \(X\left ( x \right )\propto e^{-n\pi\frac{x}{b}}\). A solução genérica é, então:
\(\varphi \left ( x,y \right )=\sum_{n=1}^{\infty }A_ne^{-n\pi\frac{x}{b}}\sin\left ( n\pi\frac{y}{b} \right )\)
onde os coeficientes são constantes que se determinam pela 2.ª condição fronteira:
\(\varphi \left ( 0,y \right )=V_0=\sum_{n=1}^{\infty }A_n\sin\left ( n\pi\frac{y}{b} \right )\; \; \; 0<\)\(y<\)\(b\)
As funções trigonométricas no segundo membro são ortogonais no intervalo. Assim:
\(A_n=\frac{2V_0}{b}\int_{0}^{b}dy\sin\left ( n\pi\frac{y}{b} \right )=\frac{2V_0}{n\pi}\left [ 1-\cos \left ( n\pi \right ) \right ]=\frac{4V_0}{n\pi}n\) ímpar
sendo nulos para n par. Deste modo, a solução completa fica:
\(\varphi \left ( x,y \right )=\frac{4V_0}{\pi}\sum_{n\; impar}^{\infty }\frac{e^{-n\pi\frac{x}{b}}}{n}\sin\left ( n\pi\frac{y}{b} \right )=\frac{2V_0}{\pi}\textrm{arctg}\left ( \frac{\sin\left ( \pi\frac{y}{b} \right )}{sh\left ( \pi\frac{x}{b} \right )} \right )\)
A conclusão mais importante deste resultado é o rápido decréscimo do potencial com a distância ao condutor ao potencial \(V_0\) — as paredes laterais, ligadas à terra, blindam aquele potencial para distâncias da ordem da distância entre as paredes.
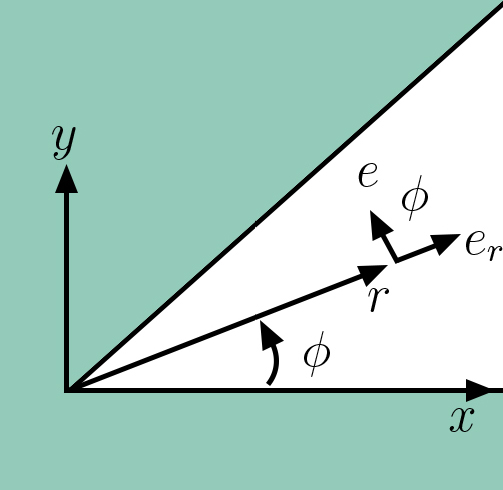
A FIGURA 12 representa uma cunha (abertura \(\beta\)) cavada num bloco metálico mantido ao potencial nulo. Um campo exterior (não representado) origina uma distribuição de cargas nos condutores, sendo apenas esta distribuição o objecto de análise. O potencial \(\varphi \) é não nulo apenas dentro da cunha e obedece às seguintes condições (usam-se coordenadas cilíndricas):
\(\Delta \varphi =\frac{1}{r}\frac{\partial }{\partial r}\left ( r\frac{\partial \varphi }{\partial r} \right )+\frac{1}{r^{2}}\frac{\partial ^{2}\varphi }{\partial \phi^{2}}=0\)
\(\varphi\left ( r,0 \right )=\varphi\left ( r,\beta \right )=0\)
As condições fronteira sugerem a separação de variáveis: \(\varphi\left ( r,\phi \right )=R\left ( r,\phi \right )=R\left ( r \right )\Phi \left ( \phi \right )\)
Procedendo como atrás e designando por \(k^2\) a constante de separação, obtém-se:
\(\frac{d^{2}\Phi }{d\phi^{2}}+k^{2}\Phi =0\)
\(r\frac{d}{dr}\left ( r\frac{dR}{dr} \right )-k^{2}R=0\)
com as condições fronteira \(\Phi \left ( 0 \right )=\Phi \left ( \beta \right )=0\). Assim, a solução da 1.ª equação anterior é \(\Phi \left ( \phi \right )\propto \sin\left ( k\phi \right )\) com \(\sin\left ( k\beta \right )=0\) e, portanto, \(k=\frac{n\pi}{\beta}\), com \(n = 1, 2, 3, ...\). Quanto à 2.ª equação, a solução é combinação linear de \(r^k\) e \(r^−k\), devendo ignorar-se a segunda função por divergir na origem. Deste modo, a solução geral do problema é:
\(\varphi\left ( r,\phi \right )=\sum_{n}^{}A_nr^{\frac{n\pi}{\beta}}\sin\left ( n\pi\frac{\phi}{\beta} \right )\)
As constantes \(A_n\) poderão ser determinadas se se conhecer a carga total no bloco; será, aqui, ignorado esse cálculo. Interessa mais determinar a densidade de carga na superfície do condutor que limita a cunha:
\(\frac{\rho _{s}\left ( r,0 \right )}{\varepsilon _{0}}=E_{\phi}\left ( r,0 \right )=-\frac{1}{r}\left ( \frac{\partial \varphi}{\partial \phi} \right )_{\phi =0}=\sum_{n}^{}\frac{n\pi}{\beta}A_nr^{\frac{n\pi}{\beta}-1}\)
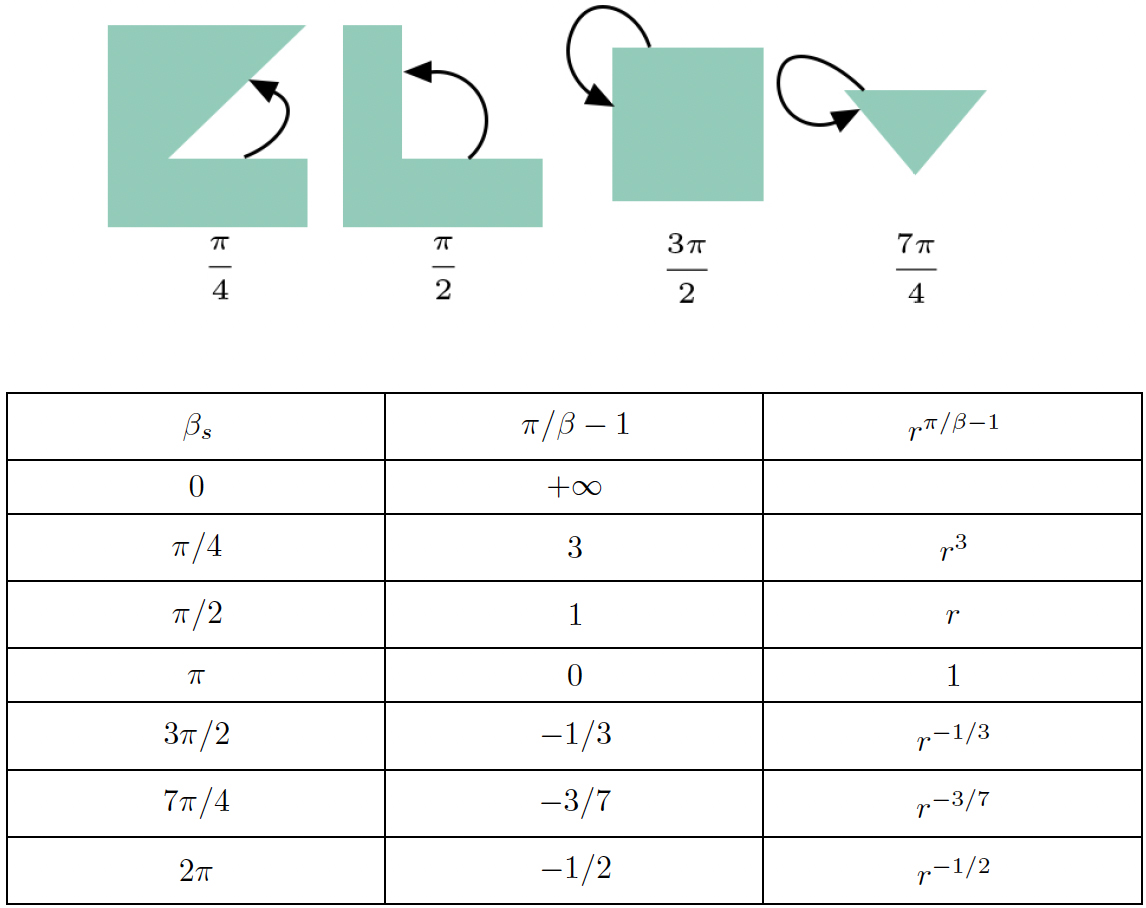
Nas vizinhanças da cunha, o primeiro termo é dominante e poderá divergir se \(\beta\) for suficientemente grande, originando uma acumulação de carga junto da cunha, efeito conhecido por poder das pontas, princípio de funcionamento dos pára-raios. A FIGURA 13 e a tabela anexa ilustram estas considerações.
O método das imagens e o método da separação de variáveis não estão restritos à Eletrostática. O método das imagens, baseado, como está, numa solução em busca de um problema, tem um âmbito de aplicação relativamente restrito. Pelo contrário, o método de separação de variáveis atravessa toda a Física empregando-se na Mecânica Clássica ou Quântica, em Mecânica de Fluidos, na propagação de ondas de diversas naturezas, etc. Como tal, este método será encontrado no tratamento de outros tópicos de interesse.
Apêndice — Demostração da unicidade de solução em Eletrostática
Com efeito, admita-se que existem duas soluções independentes \(\varphi_1\) e \(\varphi_2\) da equação (1) sujeita às condições fronteira equações (2) e (3), considerando-se a FIGURA 1 como exemplo típico mas sem perda de generalidade. Então, \(\varphi=\varphi_1-\varphi_2\) deve satisfazer:
\(\Delta\varphi=0\)
no espaço livre (vazio); e também:
\(\varphi=0\) no Condutor A
\(\int_{\Sigma _{B}}^{}dS\vec{n}\cdot\bigtriangledown \varphi=0\) (10)
Considere-se, agora, a energia eletrostática para este campo \(\varphi\):
\(U_e=\int dV\frac{\varepsilon _0}{2}\vec{E}^{2}=-\int dV\frac{\varepsilon _{0}}{2}\vec{E}\cdot \bigtriangledown \varphi=-\frac{\varepsilon _0}{2}\int dV\bigtriangledown \cdot \left ( \varphi \vec{E} \right )+\frac{\varepsilon _0}{2}\int dV\varphi\bigtriangledown \cdot \vec{E}\)
O último termo é nulo porque \(\vec{E}=0\) dentro dos condutores e \(\bigtriangledown \cdot \vec{E}=-\Delta\varphi =0\) no espaço livre. O penúltimo termo também é nulo porque, usando o teorema de Gauss obtém- se (versores \(\vec{n}\) dirigidos para o exterior das superfícies):
\(\int dV\bigtriangledown \cdot\left ( \varphi \vec{E} \right )=-\int_{\Sigma _{A}}^{}dS\vec{n}\cdot\vec{E}\varphi-\int_{\Sigma _B}^{}dS\vec{n}\cdot \vec{E}\varphi\)
Ora, pelas condições (10), é \(\varphi=0\) em \(\Sigma _A\), o que anula o primeiro integral, e como \(\varphi\) é constante em \(\Sigma _B\), o outro integral fica \(\varphi\int_{\Sigma _{B}}^{}dS\vec{n}\cdot \vec{E}=-\varphi\int_{\Sigma _{B}}^{}dS\vec{n}\cdot\bigtriangledown \varphi\) também nulo pelas mesmas condições. Assim, é \(U_e= 0\), mas \(U_e\) só faz intervir o quadrado do campo, pelo que tem de ser \(\vec{E}=0\), i.e., \(\vec{E}_{1}=\vec{E}_{2}\), contrariando a hipótese de haver duas soluções distintas para o problema eletrostático.
Referências
- ↑ LAGE, E., Os fundamentos do eletromagnetismo, Rev. Ciência Elem., V9(1):016. (2021). DOI: 10.24927/rce2021.016.
- ↑ LAGE, E., Eletrostática, Rev. Ciência Elem., V9(1):015. (2021). DOI: 10.24927/rce2021.015.
- ↑ LAGE, E., Gradiente, divergência e rotacional, Rev. Ciência Elem., V8(2):029. (2020). DOI: 10.24927/rce2020.029.
- ↑ LAGE, E., Gradiente, divergência e rotacional, Rev. Ciência Elem., V8(2):029. (2020). DOI: 10.24927/rce2020.029.
Criada em 11 de Março de 2020
Revista em 22 de Fevereiro de 2021
Aceite pelo editor em 15 de Março de 2022
