Centro de massa
Referência : Araújo, M., (2013) Centro de massa, Rev. Ciência Elem., V1(1):011
Autor: Mariana de Araújo
Editor: Joaquim Agostinho Moreira
DOI: [http://doi.org/10.24927/rce2013.011]

O centro de massa de um sistema de N corpos pontuais ou de um corpo macroscópico é um ponto representativo do movimento global de translação do corpo, ao qual é atribuída a massa total do sistema. Considera-se que todas as forças externas que actuam no corpo são aplicadas neste ponto, e o seu movimento é dado pela segunda lei de Newton. Coincide com o centro geométrico do corpo nos casos de elevada simetria e quando todas as partículas do sistema tiverem a mesma massa ou de a massa estar uniformemente distribuída pelo corpo.
Índice |
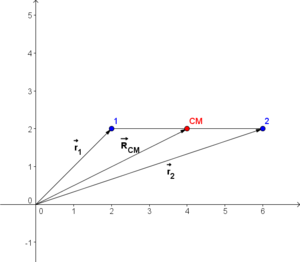
Posição do CM
A sua posição é definida como a média ponderada pela massa de cada partícula das posições de todas as partículas que constituem o corpo, e a sua massa como a massa total do corpo. Para um corpo de N partículas:
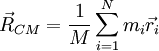
em que M é a massa total, 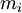 é a massa da partícula i e
é a massa da partícula i e 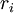 a sua posição.
a sua posição.
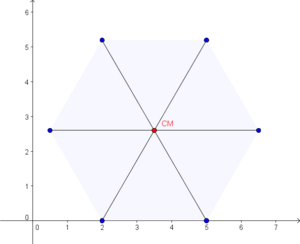
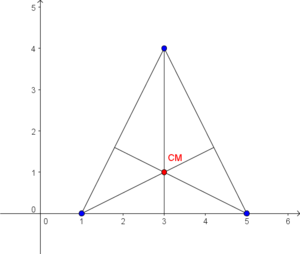
Para sistemas de N partículas de igual massa que formam um polígono de N vértices, o centro de massa coincidirá com o centro geométrico do objecto, como ilustrado abaixo. Também é verdade para sólidos em que a distribuição de massa é uniforme (isto é, quaisquer duas partes do corpo com volumes iguais têm massas iguais).
Se estas distribuições fossem uma linha, hexágono ou triângulo com a massa distribuída uniformemente pelo plano, teríamos o centro de massa no mesmo sítio, independentemente da massa total. No entanto, não podemos utilizar a forma dada acima para o cálculo analítico da posição, pois o corpo seria uma distribuição contínua de massa, e não um conjunto discreto de partículas. Nestes casos, define-se uma função densidade de massa do corpo, 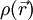 que em cada ponto do corpo na posição
que em cada ponto do corpo na posição 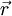 tem o valor
tem o valor 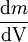 , em que
, em que 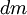 e
e 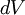 são, respectivamente, a massa e o volume do elemento infinitesimal do corpo nessa posição.
são, respectivamente, a massa e o volume do elemento infinitesimal do corpo nessa posição.
No caso discreto, em que o corpo é constituído por N partículas de massa 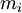 na posição
na posição 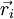 , a função densidade de massa é simplesmente
, a função densidade de massa é simplesmente 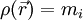 se
se 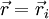 e 0 se
e 0 se 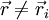 .
.
No caso de um corpo de massa M e volume V em que a massa está distribuída uniformemente, temos 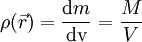 .
.
Tendo isto em consideração, para um corpo contínuo de densidade de massa 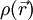 , que ocupa um volume V:
, que ocupa um volume V:
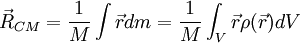
O símbolo 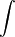 representa a operação de integrar (equivale a somar todos os valores da função no intervalo considerado) a função
representa a operação de integrar (equivale a somar todos os valores da função no intervalo considerado) a função 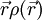 sobre todo o volume V.
sobre todo o volume V.
Note-se que em nenhum dos casos, discreto ou contínuo, é obrigatório que o centro de massa esteja localizado no volume que constitui o corpo.
Velocidade e quantidade de movimento do CM
Derivando 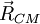 em ordem ao tempo obtemos as relações (também válidas na formulação integral)
em ordem ao tempo obtemos as relações (também válidas na formulação integral)
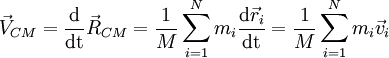
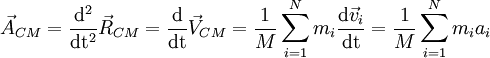
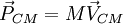
Centro de gravidade
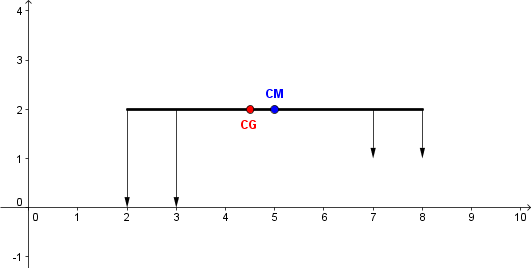
Centro de gravidade é o ponto por onde se deve fixar o objecto de modo a que este não rode sob a acção do campo gravítico, i.e., se for aplicada uma força igual e simétrica à força gravítica total, de modo a que a força resultante das duas é nula nesse ponto, também o momento da força gravítica é nulo. Nos casos em que o campo gravítico é uniforme no volume onde se encontra o corpo, o centro de gravidade e o centro de massa coincidem. Caso contrário, o centro de gravidade irá estar deslocado.
Consideremos o exemplo da figura. A barra tem uma distribuição de massa uniforme, no entanto, o campo gravítico na primeira metade é o dobro do campo na segunda (a força gravítica está ilustrada pelos vectores na imagem). Caso a barra seja fixa na posição do centro de massa, irá existir um momento de força não nulo que fará a barra rodar, apesar da força exercida pelo suporte ser igual à força gravítica total exercida na barra. Mas se o suporte for colocado no ponto assinalado como centro de gravidade, a barra irá ficar em repouso, pois o momento de força total também é nulo.
Referências
1. Feymnan, R., Leighton, R. & Sands, M., The Feymnan Lectures on Physics, Vol. 1, Addison-Wesley Publishing, 1963.
2. Deus, J.D., Pimenta, M., Noronha, A., Peña, T. & Brogueira, P., Introdução à Física, 2ª edição, McGraw-Hill, 2000.
Criada em 04 de Novembro de 2010
Revista em 13 de Fevereiro de 2011
Aceite pelo editor em 13 de Fevereiro de 2011