Axiomática da Probabilidade (Axiomática de Kolmogorov)
Referência : Martins, E.G.M., (2015) Axiomática da Probabilidade (Axiomática de Kolmogorov), Rev. Ciência Elem., V3(1):077
Autores: Maria Eugénia Graça Martins
Editor: José Francisco Rodrigues
DOI: [http://doi.org/10.24927/rce2015.077]
Considere-se um espaço de resultados \(\rm S\), finito, e um conjunto A de subconjuntos de \(\rm S\) – acontecimentos - que satisfaça as seguintes condições:
- a) O acontecimento certo \(\rm S\), pertence a A.
- b) Se um acontecimento \(\rm A\) pertence a A, então o seu complementar (ver Operações com acontecimentos) \(\bar{\rm{A}}\) também pertence a A.
- c) Se dois acontecimentos pertencem a A, então a sua união \({\rm{A \cup B}}\) (ver Operações com acontecimentos) também pertence a A.
Ao par (\(S\), A), chamamos espaço de acontecimentos.
Uma medida de Probabilidade \(\rm{P}\) é uma função de conjunto, isto é, definida em A, que a cada elemento \(\rm A\) pertencente a A associa um número real que se chama Probabilidade de \(\rm A\) e se representa por \(\rm{P(A)}\), satisfazendo as seguintes condições ou axiomas:
1º axioma - A probabilidade de qualquer acontecimento é maior ou igual a zero
- \({\rm{P}}{\rm{(A) ≥ 0}}\).
2º axioma - A probabilidade do acontecimento certo \(\rm S\), é 1:
- \({\rm{P(S) = 1}}\).
3º axioma - Dados dois acontecimentos disjuntos, a probabilidade da sua união é igual à soma das probabilidades de cada um
- Se \({\rm{A}{\rm{\cap}}{\rm{B}} = \emptyset\quad\Rightarrow\quad {\rm{P(A \cup B)}} = {\rm{P(A) + P(B)}}}\)
No caso de S não ser finito, a condição c) é substituída pela condição
- c*) Se \(\rm{A_1}\), \(\rm{A_2}\), \(\rm{A_3}\), ... pertencem a A então \(\bigcup\limits_{{\rm{i}} = {\rm{1}}}^\infty {{{\rm{A}}_{\rm{i}}}} \) também pertence a A
e o 3º axioma é substituído pelo seguinte axioma:
3º axioma* - Se \(\rm{A_1}\), \(\rm{A_2}\), \(\rm{A_3}\), ... são acontecimentos disjuntos dois a dois, então
- \({\rm{P(}}\bigcup\limits_{{\rm{i}} = {\rm{1}}}^\infty {{{\rm{A}}_{\rm{i}}}}{\rm{)}} = \sum\limits_{{\rm{i}} = {\rm{1}}}^\infty {{\rm{P(}}{{\rm{A}}_{\rm{i}}}{\rm{)}}}\)
Os axiomas anteriores são conhecidos como a axiomática de Kolmogorov.
A probabilidade frequencista, laplaciana e subjetiva, verificam a axiomática de Kolmogorov.
Como consequência da axiomática anterior, resultam as seguintes propriedades para a Probabilidade, que facilmente se ilustram com a ajuda de diagramas de Venn e se demonstram a seguir:
Propriedades da Probabilidade
1. Probabilidade do acontecimento impossível, \({\rm{P}}(\emptyset)=0\)
| pois \({\rm{S}}= \left({\rm{S}} \cup \emptyset \right)\) e como \({\rm{S}}\) e \(\emptyset\) são disjuntos, pelo 3º axioma vem | \[\rm P\left({\rm{S}} \cup \emptyset \right) = \rm P\left({\rm{S}}\right) + \rm P\left(\emptyset\right)\] |
| \(\quad \quad \quad \quad \quad \ = 1\). |
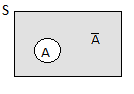
2. Probabilidade do acontecimento complementar, \({\rm{P}}(\bar{\rm{A}})=1- {\rm{P(A)}}\)
| pois \({\rm{S}} = {\rm{A}} \cup \bar{\rm{A}}\) e como \({\rm{A}}\) e \(\bar{\rm{A}}\) são disjuntos vem | \[\rm P\left({\rm{A}} \cup \bar{{\rm{A}}}\right) = \rm P\left(\rm{A}\right) + \rm P\left(\bar{\rm{A}}\right)\] |
| \(\quad \quad \quad \quad \quad \quad \ = 1\). |
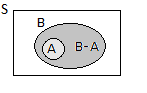
3. Se \({\rm{A}}\) implica \({\rm{B}}\) (ver Operações com acontecimentos), ou seja, \({\rm{A}} \subseteq {\rm{B}}\), então \({\rm{P(A)}} \leq {\rm{P(B)}}\)
pois \({\rm{B}} = {\rm{A}} \cup {\rm{(B - A)}}\) e como \({\rm{A}}\) e \({\rm{(B-A)}}\) são disjuntos vem:
| \(\rm P\left({\rm{B}}\right) = \rm P\left(\rm{A}\right) + \rm P\left({\rm{(B-A)}}\right)\) | |
| \(\quad \quad \quad \ \geq \rm P\left({\rm{A}}\right)\) porque \(\rm P\left({\rm{(B-A)}}\right)\geq 0\) pelo 1º axioma. |
4. Para qualquer acontecimento \({\rm{A}}\), tem-se \(0 \leq \rm{P(A)} \leq 1\)
Esta propriedade é consequência da propriedade anterior, dado que \({\rm{A}} \subseteq {\rm{S}}\).
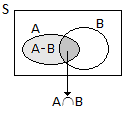
5. Dados dois acontecimentos \({\rm{A}}\) e \({\rm{B}}\) quaisquer, tem-se \({\rm{P(A-B)}}= {\rm{P(A)-P(A \cap B)}}\)
pois \({\rm{A}}= {\rm{(A-B)}}\cup {\rm{(A\cap B)}}\), com \({\rm{(A-B)}}\) e \({\rm{A \cap B}}\) disjuntos.
6. A probabilidade da união de dois acontecimentos \({\rm{A}}\) e \({\rm{B}}\) quaisquer é \({\rm{P(A \cup B)}}= {\rm{P(A)}}+{\rm{P(B)}}-{\rm{P(A\cap B)}}\)
pois \({\rm{A \cup B}}= {\rm{(A-B)\cup(A\cap B)\cup(B-A)}}\), com \({\rm{(A-B)}}\), \({\rm{A\cap B}}\) e \({\rm{(B-A)}}\) disjuntos dois a dois e tendo em consideração a propriedade anterior.
Esta fórmula generaliza-se ao caso de três acontecimentos \(\rm A\), \(\rm B\) e \(\rm C\)
\({\rm{P(A \cup B \cup C)}}= {\rm{P(A)}}+{\rm{P(B)}} + {\rm{P(C)}}-{\rm{P(A\cap B)}} - {\rm{P(A\cap C)}} - {\rm{P(B\cap C)}} + {\rm{P(A \cap B \cap C)}}\)
ou a mais acontecimentos, dando lugar à Fórmula de Daniel da Silva
Ver
Referências
1. GRAÇA MARTINS, M. E., MONTEIRO, C., VIANA, P. V., TURKMAN, M. A. A. (1999) – Probabilidades e Combinatória. Ministério da Educação, Departamento do Ensino Superior. ISBN: 972-8417-33-0. Depósito Legal 143440/99.
2. MANN, P. S. (1995) – Introductory Statistics, 2nd edition. John Wiley & Sons, Inc. ISBN: 0-471-31009-3.
3. PESTANA, D., VELOSA, S. (2010) – Introdução à Probabilidade e à Estatística, Volume I, 4ª edição, Fundação Calouste Gulbenkian. ISBN: 978-972-31-1150-7. Depósito Legal 311132/10.
4. SILVA,J.S. (1975) - Compêndio de Matemática, 1º Volume (2º TOMO) Gabinete de Estudos e Planeamento do Ministério da Educação e Cultura.
5. SILVA,J. - "Cálculo das Probabilidades", (Curso do Instituto Superior de Agronomia, 1955), in Textos Didácticos, Vol. 1, Fundação Calouste Gulbenkian, Lisboa, 1999.
Criada em 29 de Março de 2012
Revista em 22 de Maio de 2013
Aceite pelo editor em 22 de Maio de 2013