Ângulos de Euler
Referência : Lage, E., (2020) Ângulos de Euler, Rev. Ciência Elem., V8(3):043
Autor: Eduardo Lage
Editor: José Ferreira Gomes
DOI: [http://doi.org/10.24927/rce2020.043]

Resumo
Dois observadores, cada um munido com um sistema triretangular de eixos cartesianos, podem determinar exatamente a posição do mesmo ponto no espaço. Mas como sabem esses observadores que se trata do mesmo ponto quando as coordenadas que obtêm são diferentes? É, evidentemente, necessário que cada observador saiba não só a posição do outro como também a orientação de um sistema de eixos em relação ao outro. É esta última questão que é aqui considerada e nos leva à introdução dos ângulos de Euler, três ângulos que determinam univocamente aquela orientação através de rotações em eixos distintos. Não se trata, apenas, de um problema matemático, com imediato interesse na dinâmica de um sólido, porque as suas aplicações se estendem à navegação aérea e marítima, à astronáutica e astronomia.
A FIGURA 1 mostra como a orientação do sistema de eixos \(O_{xyz}\) pode ser definida em relação ao referencial \(OXY\) Z pelos três ângulos de Euler, habitualmente designados por \(\phi\), \(\theta\), \(\psi \). Esta definição não é única, mas é a mais comum. Passamos a descrever como são definidos aqueles três ângulos, chamando a atenção que todos eles fazem intervir rotações geralmente no sentido anti-horário.
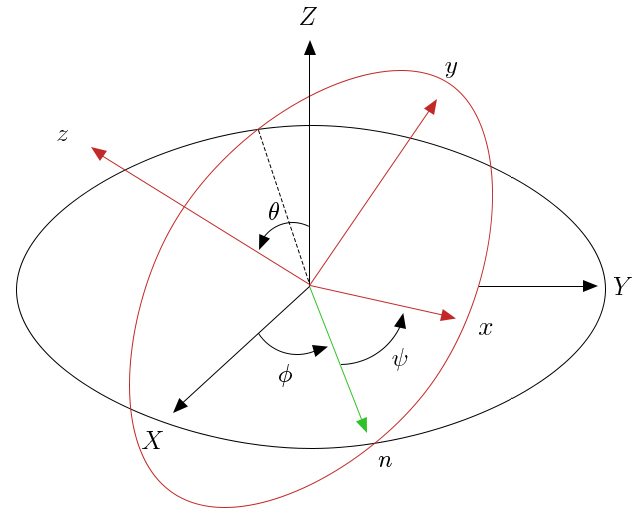
O primeiro passo consiste numa rotação de um ângulo \(\phi\) em torno do eixo \(Z\). Nesta rotação, o eixo \(X\) é levado para uma posição designada por linha dos nodos, onde é marcado o versor \(\vec{n}\) obtido por aquela rotação do versor do eixo X.
É evidente que as componentes de \(\vec{n}\) no referencial \(OXYZ\) são:
\(\vec{n}=\left ( cos\phi,sen\phi,0 \right )\) (1)
Designemos por \(Oxy′z′\) o sistema de eixos obtido por esta rotação de \(OXYZ\) (FIGURA 2D)). A relação entre as coordenadas do mesmo ponto nestes dois sistemas pode escrever-se sob a forma matricial seguinte:
\(\begin{bmatrix} X\\ Y\\ Z \end{bmatrix}=\begin{bmatrix} cos\phi & -sen\phi & 0\\ sen\phi & cos\phi & 0\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x'\\ y'\\ z' \end{bmatrix}\) (2)
A seguir, efectuamos uma rotação de � em torno da linha dos nodos. O sistema de eixos \(Ox′y′z′\) determina, por esta rotação, o sistema \(Ox”y”z”\) (FIGURA 2B)). A relação entre as coordenadas do mesmo ponto nestes dois sistemas, é:
\(\begin{bmatrix} x'\\ y'\\ z' \end{bmatrix}=\begin{bmatrix} 1 & 0 & 0\\ 0 & cos\theta & -sen\theta\\ 0 & sen\theta & cos\theta \end{bmatrix}\begin{bmatrix} x"\\ y"\\ z" \end{bmatrix}\) (3)
Finalmente, rodamos de \(\phi\) em torno do eixo \(z”\), levando o sistema de eixos \(Ox”y”z”\) ao sistema de eixos pretendido \(Oxyz\) (FIGURA 2C)), obtendo-se, assim, a relação entre as coordenadas do mesmo ponto nestes dois referenciais:
\(\begin{bmatrix} x"\\ y"\\ z" \end{bmatrix}=\begin{bmatrix} cos\psi & -sen\psi & 0\\ sen\psi & cos\psi & 0\\ 0 & 0 & 1 \end{bmatrix}\) (4)
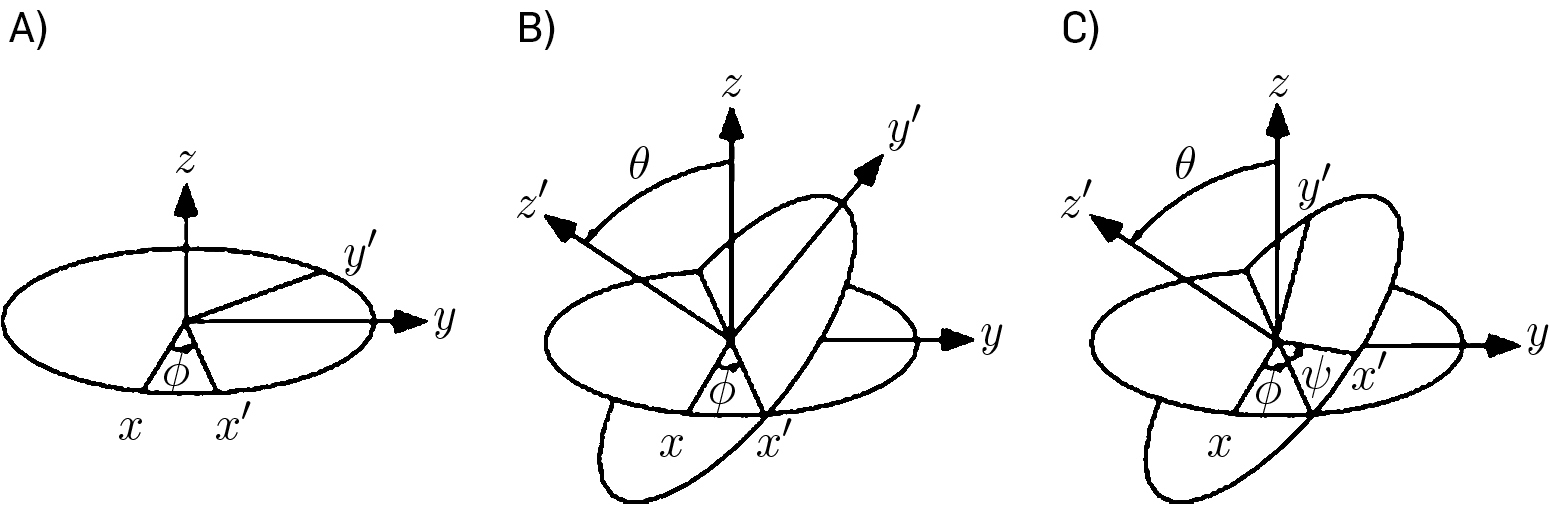
Note-se que a linha dos nodos é perpendicular ao plano definido pelos eixos \(Z\equiv z'\) e \(z"\equiv z\).
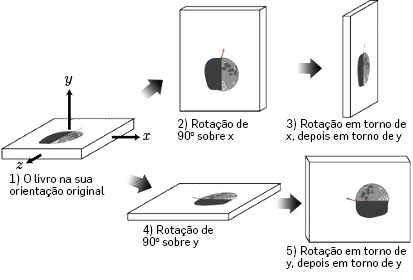
É importante sublinhar que a ordem em que são aplicadas estas rotações não é arbitrária: rotações finitas não comutam (FIGURA 3), o mesmo acontecendo às suas matrizes representativas. Contudo, rotações infinitesimais comutam porque termos cruzados no produto das matrizes são de segunda ordem ou superior.
Estas considerações vão-nos permitir obter uma importante expressão para o vector rotação instantânea \(\vec{\omega}\) (Ver “Sólido rígido”) de que recordamos a sua definição:
\(\delta\omega\equiv \vec{\omega}\delta t\) (5)
é a rotação infinitesimal do sólido, no curto intervalo de tempo \(\delta t\), de grandeza \(\left | \delta \Omega \right |\), como um saca-rolhas que progrida no sentido de \(\vec{\omega}\). Imaginemos que os eixos xyz, atrás referidos, são eixos do sólido; é frequente considerar a origem no centro de massa e fazer coincidir estes eixos com os eixos principais dinércia, embora nem uma nem outra destas identificações seja necessária. No movimento do sólido, estes eixos rodam no espaço (em relação ao referencial fixo \(OXYZ\)), pelo que os ângulos de Euler dependem do tempo. Assim, durante o curto intervalo de tempo \(\delta t\), estes ângulos sofrem acréscimos \(\delta\phi=\phi \delta t,\delta \theta=\theta\delta t ,\delta \psi=\psi\delta t\) originando rotações em torno dos eixos atrás identificados. Lembrando: \(\delta\psi\) é uma rotação em torno do eixo \(Z\), fixo, contribuindo com \(\delta\psi\vec{e}_{Z}=\psi\vec{e}_{Z}\delta t\); \(\delta\vec{\Omega}\) é uma rotação em torno da linha dos nodos, contribuído com \(\theta\vec{n}\delta t\); e \(\delta\psi\) é uma rotação em torno do eixo \(z\) (do sólido), contribuindo com \(\psi\vec{e}_{z}\delta t\)(\(\vec{e}_{Z}\) e \(\vec{e}_{z}\) são versores nos respectivos eixos). Assim:
\(\delta\bar{\Omega}=\left ( \psi\vec{e}_{Z}+\theta\vec{n}+\psi\vec{e}_{z} \right )\delta t\)
Comparando com a eq (5), obtemos finalmente:
\(\vec{\omega}=\psi\vec{e}_{Z}+\theta\vec{n}+\psi\vec{e}_{z}\) (6)
Este resultado é fundamental para o estudo de diversas aplicações da dinâmica de sólidos rígidos.
Referências
- HELBERT, G. Classical Mechanics (2nd ed.), Reading MA: Addison Wesley, ISBN: 978-0-201-02918-5. 1980.
Criada em 21 de Abril de 2020
Revista em 24 de Abril de 2020
Aceite pelo editor em 30 de Setembro de 2020
